辽宁省沈阳市2020届高三三模考试数学（理科）试题 Word版含解析

辽宁省沈阳市2020届高三三模考试数学（理科）试题 Word版含解析

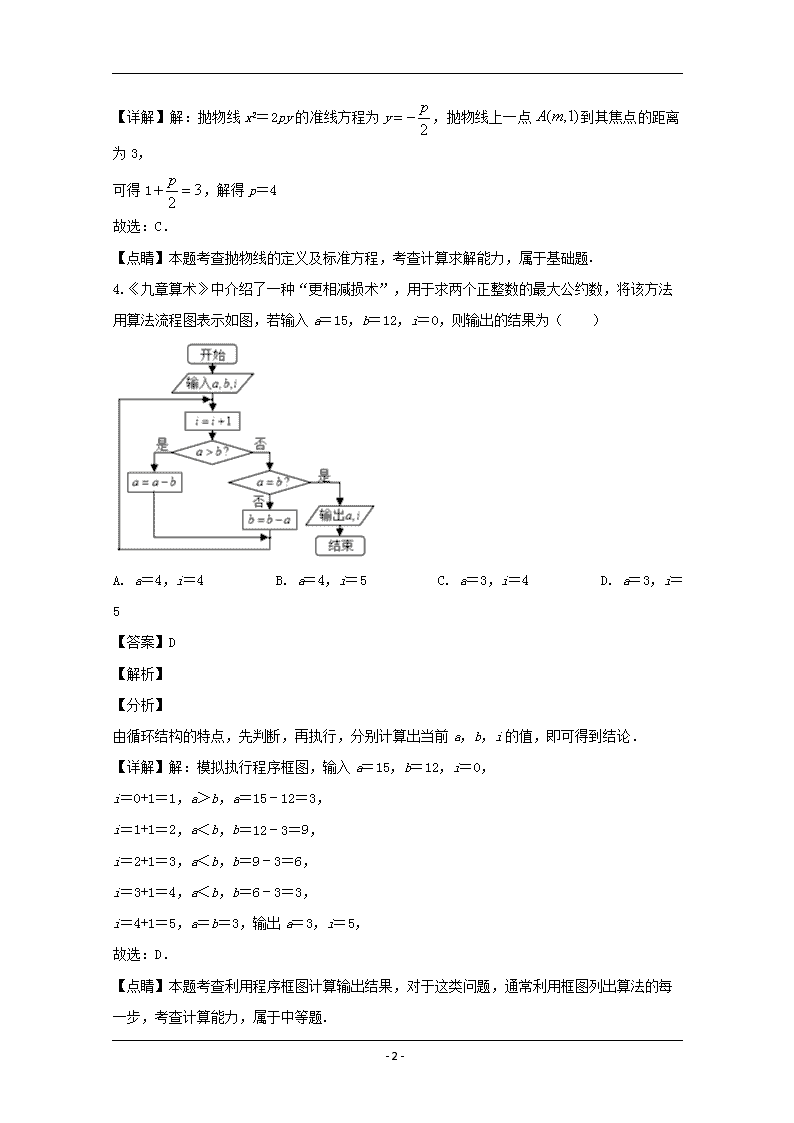
- 1 - 2020 年高考数学三模试卷（理科） 一、选择题（共 12 小题）. 1.已知集合 { | ( 1)( 2) 0}, { | 0}     M x x x N x x ，则（ ） A. N M B. M N C. M N   D. M N R 【答案】B 【解析】 【分析】 求解出集合 M ，根据子集的判定可得结果. 【详解】由题意知：      1 2 0 1 2M x x x x x       ，则 M N 本题正确选项： B 【点睛】本题考查集合间的关系，属于基础题. 2.复数 1 2z i  ，若复数 1z ， 2z 在复平面内的对应点关于虚轴对称，则 1 2z z  （ ） A. 5 B. 5 C. 3 4i  D. 3 4i 【答案】A 【解析】 【分析】 首先求出复数 2 2z i   ，再根据复数的代数形式的乘法运算法则计算可得； 【详解】解：由题意可知 2 2z i   ，所以 2 1 2 (2 i)( 2 i) 4 i 5z z          ， 故选：A． 【点睛】本题考查复数的几何意义的应用，以及复数代数形式的乘法运算，属于基础题. 3.已知抛物线 x2＝2py 上一点 A（m，1）到其焦点的距离为 3，则 p＝（ ） A. 2 B. ﹣2 C. 4 D. ±4 【答案】C 【解析】 【分析】 求出抛物线的准线方程，利用抛物线的定义，转化求解即可． 【详解】解：抛物线 x2＝2py 的准线方程为 y 2 p  ，抛物线上一点 ( ,1)A m 到其焦点的距离为 - 2 - 3， 可得 1 32 p  ，解得 p＝4 故选：C． 【点睛】本题考查抛物线的定义及标准方程，考查计算求解能力，属于基础题. 4.《九章算术》中介绍了一种“更相减损术”，用于求两个正整数的最大公约数，将该方法 用算法流程图表示如图，若输入 a＝15，b＝12，i＝0，则输出的结果为（ ） A. a＝4，i＝4 B. a＝4，i＝5 C. a＝3，i＝4 D. a＝3，i ＝5 【答案】D 【解析】 【分析】 由循环结构的特点，先判断，再执行，分别计算出当前 a，b，i 的值，即可得到结论． 【详解】解：模拟执行程序框图，输入 a＝15，b＝12，i＝0， i＝0+1＝1，a＞b，a＝15﹣12＝3， i＝1+1＝2，a＜b，b＝12﹣3＝9， i＝2+1＝3，a＜b，b＝9﹣3＝6， i＝3+1＝4，a＜b，b＝6﹣3＝3， i＝4+1＝5，a＝b＝3，输出 a＝3，i＝5， 故选：D． 【点睛】本题考查利用程序框图计算输出结果，对于这类问题，通常利用框图列出算法的每 一步，考查计算能力，属于中等题. 5.数学家华罗庚倡导的“0.618 优选法”在各领域都应用广泛,0.618 就是黄金分割比 - 3 - 5 1 2m  的近似值,黄金分割比还可以表示成 2sin18,则 2 2 4 2cos 27 1 m m   ( ). A. 4 B. 5 1 C. 2 D. 5 1 【答案】C 【解析】 【分析】 把 2sin18m   代入 2 2 4 2cos 27 1 m m  中，然后结合同角三角函数基本关系式与倍角公式化简求 值. 【详解】解：由题可知 5 12sin18 2m    ， 所以 2 4sin18m  . 则 2 2 2 2 4 2sin18 4 4sin 18 2cos 27 1 2cos 27 1 m m     2sin18 2cos18 cos54    2sin36 cos54   2 . 故选：C. 【点睛】本题考查三角函数的恒等变换与化简求值，考查同角三角函数基本关系式与倍角公 式的应用，是基础题． 6.已知某不规则几何体三视图如图，其中俯视图中的圆弧为 1 4 圆周，则该几何体的侧面积为 （ ） - 4 - A. 34 4  B. 7 2 2  C. 7 5 2 4  D. 7 5 2 8  【答案】C 【解析】 【分析】 首先把三视图转换为直观图，是一个三棱锥体 S-ABO 和一个 1 4 圆锥组成的几何体，然后再求 几何体的侧面积． 【详解】由几何体的三视图转换为直观图为：由一个三棱锥体 S-ABO 和一个 1 4 圆锥组成的几 何体． 如图所示： 所以该几何体的侧面积为 S 侧 1 4      SAC SABS S OC SC ． 1 1 3 2 1 5 7 52 2 22 2 2 4 2 4            . 故选：C． 【点睛】本题主要考查三视图还原几何体以及几何体侧面积的求法，还考查了空间想象和运 算求解的能力，属于基础题. 7.设函数 f（x）＝cos2x+bsinx，则“b＝0”是“f（x）的最小正周期为π”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 - 5 - 【答案】C 【解析】 【分析】 直接利用正弦型函数的性质的应用和四个条件的应用求出结果． 【详解】当 0b  时，函数   2cos sinf x x b x  2 1 2 2 cos xcos x   ，所以函数的最小正 周期为 2 2   ，   2cos sinf x x b x  1 2 sin2 cos x b x  ， 当 0b≠ 时，函数的最小正周期为π和 2π的最小公倍数，即为 2π， 当函数的最小正周期为π时，可得 0b  ， 故函数   2cos sinf x x b x  ，则“ 0b  ”是“f（x）的最小正周期为π”的充要条件． 故选：C 【点睛】本题考查的是三角函数的性质和充要条件的判定，属于基础题. 8.2020 年初，新型冠状肺炎在欧洲爆发后，我国第一时间内向相关国家捐助医疗物资，并派 出由医疗专家组成的医疗小组奔赴相关国家．现有四个医疗小组甲、乙、丙、丁，和有 4 个 需要援助的国家可供选择，每个医疗小组只去一个国家，设事件 A＝“4 个医疗小组去的国家 各不相同”，事件 B＝“小组甲独自去一个国家”，则 P（A|B）＝（ ） A. 2 9 B. 1 3 C. 4 9 D. 5 9 【答案】A 【解析】 【分析】 先求出“4 个医疗小组去的国家各不相同”且“小组甲独自去一个国家”的概率，再求“小组 甲独自去一个国家”的概率，代入条件概率公式计算即可． 【详解】事件 A＝“4 个医疗小组去的国家各不相同”，事件 B＝“小组甲独自去一个国家”， 则 P（AB） 4 4 4 3 4 32 A  ，P（B） 1 3 4 4 3 27 4 64 C   ， P（A|B）     2 9 P AB P B   ， 故选：A． - 6 - 【点睛】本题考查了条件概率的计算，考查了学生综合分析，转化划归，数学运算能力，属 于中档题 9.已知O 为 ABC 的外接圆的圆心，且3 4 5OA OB OC     ，则 C 的值为（ ） A. 4  B. 2  C. 6  D. 12  【答案】A 【解析】 【分析】 由题意首先结合平面向量数量积的运算法则确定 AOB 的大小，然后建立平面直角坐标系， 结合向量的运算法则求得 cosC 的值即可确定 C 的值. 【详解】由题意可得：| | | | | |OA OB OC    ，且 1 (3 4 )5OC OA OB     ， 2 21| | (3 4 )25OC OC OC OA OB         2 29 24 16| | | |25 25 25OA OA OB OB       2 24| | 25OC OA OB     ， 24 025 OA OB    ，∴∠AOB=90°. 如图所示，建立平面直角坐标系，设  0,1A ，  10B , ， - 7 - 由  3 4 4,3 5OA OB OC      可知： 4 3,5 5C      ，则： 4 8,5 5CA       ， 9 3,5 5CB       ， 36 24 225 25cos 24 5 3 10 5 5 CA CBC CA CB          ， 则 4C   . 故选：A. 【点睛】本题主要考查平面向量的运算法则，向量垂直的充分必要条件，由平面向量求解角 度值的方法等知识，意在考查学生的转化能力和计算求解能力. 10.我们打印用的 A4 纸的长与宽的比约为 2 ，之所以是这个比值，是因为把纸张对折，得到 的新纸的长与宽之比仍约为 2 ，纸张的形状不变．已知圆柱的母线长小于底面圆的直径长（如 图所示），它的轴截面 ABCD 为一张 A4 纸，若点 E 为上底面圆上弧 AB 的中点，则异面直线 DE 与 AB 所成的角约为（ ） A. 6  B. 4  C. 3  D. 2 3  【答案】C 【解析】 【分析】 设 CD 的中点为 O，过 E 作 EF⊥底面⊙O，连接 OE，OF，证明 OD⊥OE，计算 tan∠EDO 即可得 出答案． 【详解】∵AB//CD，∴∠EDC（或补角）为异面直线 DE 与 AB 所成的角， 设 CD 的中点为 O，过 E 作 EF⊥底面⊙O，连接 OE，OF， ∵E 是 AB 的中点，∴F 是 CD 的中点，∴CD⊥OF， 又 EF⊥平面⊙O，∴EF⊥CD， EF OF F - 8 - ∴CD⊥平面 OEF，∴OD⊥OE． 设 AD＝1，则 CD 2 ，故 OF 2 2  ，EF＝1， 于是 OE 2 22 61 ( )2 2    ， ∴tan∠EDO 6 2 3 2 2 OE OD    ， ∴∠EDO 3  ． 故选：C． 【点睛】本题考查了异面直线所成的角，解题的关键是找出与异面直线所成角相等的相交直 线所成的角，此题要求有一定的计算能力，属于中档题. 11.已知 x 与 y 之间的几组数据如表： x 1 2 3 4 y 1 m n 4 如表数据中 y 的平均值为 2.5，若某同学对 m 赋了三个值分别为 1.5，2，2.5，得到三条线性 回归直线方程分别为 1 1ˆy b x a  ， 2 2ˆy b x a  ， 3 3ˆy b x a  ，对应的相关系数分别为 1r ， 2r ， 3r ，下列结论中错误的是（ ） 参考公式：线性回归方程 ˆˆ ˆy bx a  中，其中    1 2 1 ˆ ( ) n i i i n i i x x y y b x x         ， ˆˆa y bx  ．相关系 - 9 - 数    1 2 2 1 1     ( ) ( ) n i i i n n i i i i x x y y r x x y y            ． A. 三条回归直线有共同交点 B. 相关系数中， 2r 最大 C. 1 2b b D. 1 2a a 【答案】D 【解析】 【分析】 由题意可得 5m n  ，分别取 m 与 n 的值，根据公式计算出 b1，a1，b2，a2，r1，r2，r3 的值， 逐一分析四个选项可得答案． 【详解】由样本的中心点相同，故 A 正确； 由题意，1 4 10m n    ，即 5m n  ． 若 1.5m  ，则 3.5n  ，此时 1 2 3 4 2.54x     ， 2.5y  ．               4 1 1 2.5 1 2.5 2 2.5 1.5 2.5 3 2.5 3.5 2.5 4 2.5 4 2.5 5.5i i i x x y y                    4 2 22 2 2 1 ( ) 1.5 0.5 0.5 1.5 5i i x x          ，    4 2 22 2 2 1   ( ) 1.5 1 1 1.5 6.5i i y y          则 1 5.5 1.15b   ， 1 2.5 1.1 2.5 0.25a      ， 1 5.5 0.93 5 6.5 r    ； 若 2m  ，则 3n  ，此时 1 2 3 4 2.54x     ， 2.5y  ．               4 1 1 2.5 1 2.5 2 2.5 2 2.5 3 2.5 3 2.5 4 2.5 4 2.5 5i i i x x y y                    4 2 22 2 2 1 ( ) 1.5 0.5 0.5 1.5 5i i x x          ，    4 2 22 2 2 1 ( ) 1.5 0.5 0.5 1.5 5i i y y          - 10 - 则 2 5 15b   ， 2 2.5 1 2.5 0a     ， 2 5 1 5 5 r    ； 若 2.5m  ，则 2.5n  ，此时 1 2 3 4 2.54x     ， 2.5y  ．               4 1 1 2.5 1 2.5 2 2.5 2.5 2.5 3 2.5 2.5 2.5 4 2.5 4 2.5 4.5i i i x x y y                 ， 4 2 1 ( ) 5i i x x    ，  4 22 2 1 ( ) 1.5 1.5 4.5i i y y       ， 3 4.5 0.9 5 4.5 r    ． 由以上计算可得，相关系数中， 2r 最大， 1 2b b ， 1 2a a ，故 B，C 正确，D 错误． 故选：D 【点睛】本题考查的是线性回归方程的计算和相关系数的计算，解答本题的关键是学生的计 算能力，属于基础题. 12.已知函数   3 4f x x x  ，过点  2,0A  的直线 l 与  f x 的图象有三个不同的交点，则 直线 l 斜率的取值范围为（ ） A.  1,8 B.    1,8 8,   C.    2,8 8,   D.  1,  【答案】B 【解析】 【分析】 设直线 l 的斜率为 k ，方程为  2y k x  ，由题意可得   32 4k x x x   有三个不等的实 根，显然 2x   是其中的一个根，则 2 2k x x  有两个不等的实根，且 2x   ，由判别式大 于 0 ，可得所求范围． 【详解】函数   3 4f x x x  ，可得      32 2 4 2 0f        ， 设直线 l 的斜率为 k ，方程为  2y k x  ， 由题意可得     32 4 2 2k x x x x x x      有三个不等的实根， 显然 2x   是其中的一个根， - 11 - 则 2 2k x x  有两个不等的实根，且 2x   ，即 8k  ， 由 2 2 0  x x k 的   ，可得 4 4 0k  ，解得 1k   ， 则 k 的范围是   1,8 8,   . 故选：B． 【点睛】本小题主要考查根据方程的根、函数图象的交点，考查化归与转化的数学思想方法， 属于中档题. 二、填空题：本题共 4 小题，每小题 5 分，共 20 分． 13.已知 m 是常数， 5 5 4 3 2 5 4 3 2 1 0( 1)mx a x a x a x a x a x a       ，且 1 2 3 4 5 33a a a a a     ，则 m  _____． 【答案】3 【解析】 【分析】 在已知二项式中分别取 0x  和 1x  ，联立即可求得 m 值． 【详解】在 5 5 4 3 2 5 4 3 2 1 0( 1)mx a x a x a x a x a x a       中， 取 0x  ，得 01 a  ， 取 1x  ，得 5 5 4 3 2 1 0( 1)m a a a a a a       ， 所以 5 1 2 3 4 5 ( 1) 1 33a a a a a m        ， 所以 5( 1) 32m   ，解得 3m  . 故答案为：3 【点睛】本题主要考查二项式定理的应用，对 x 恰当的赋值是解题的关键，属于基础题. 14.已知   1f x x x   ，若  2log 5 2f b  ，则 2log 1 bf      _____． 【答案】 5 2  【解析】 【分析】 由已知可得 f（x）为奇函数，结合奇函数的定义可求． - 12 - 【详解】∵   1f x x x   ， ∴    1f x x f xx       ，即 f（x）为奇函数， ∵  2 2 2 2 log log log log 2l 5 og 1 2bf b b bb     ， 则    1 log 2 log 22logb b bf f f        1log 2 log 2b b         2log 2 logb b   5 2   故答案为： 5 2  【点睛】本题主要考查奇函数的定义，属于基础题. 15.在平面直角坐标系 xOy 中，F 是双曲线   2 2 2 2 1 0 0x y a ba b   ＞ ， ＞ 的右焦点，直线 y＝2b 与双曲线交于 B，C 两点，且∠BFC＝90°，则该双曲线的离心率为_____． 【答案】 3 5 5 【解析】 【分析】 由题可知，F（c，0），把 y＝2b 代入双曲线方程可得 B,C 坐标，因为∠BFC＝90°，所以 kBF•kCF ＝﹣1，化简得 4b2＝5a2﹣c2，然后结合 b2＝c2﹣a2，计算即可得解． 【详解】解：由题意可知，F（c，0）， 把 y＝2b 代入双曲线方程可得 5x a  ，不妨设 B（ 5 2a b ， ），C（ 5 2a b， ）， 因为∠BFC＝90°，所以 kBF•kCF＝﹣1，即 2 2 1 5 5 b b a c a c       ，化简得 4b2＝5a2﹣c2， 因为 b2＝c2﹣a2，所以 2 2 9 5 c a  ， 所以离心率 3 3 5 55 ce a    ． 故答案为： 3 5 5 ． - 13 - 【点睛】本题考查直线和双曲线的位置关系，考查双曲线的离心率问题，考查学生计算求解 能力，属于中档题. 16.在△ABC 中，角 A，B，C 的对边分别为 a，b，c，设△ABC 的面积为 S，若 2 2 24sin 3sin 2sinA B C  ，则 S AB AC  的最大值为_____． 【答案】 7 2 【解析】 【分析】 由 2 2 24sin 3sin 2sinA B C  可 得 2 2 24 3 2a b c  ， 然 后 2 22 2 22 2 1 11 1 2 4 24 2 2cos 2 2 2 4 b c aA bc b bc b c cb c      ， 然 后 2 si 1 1 12 12cos 2 cos nc b sinAS c b cosA A AAB AC A         ，即可得到答案. 【详解】△ABC 中， 2 2 24sin 3sin 2sinA B C  ， 所以 2 2 24 3 2a b c  ； 所以 2 22 2 22 2 1 11 1 2 4 24 2 2cos 2 2 2 4 b c aA bc b bc b c cb c      ， 当且仅当 2 21 1 4 2b c 即 2b c 时等号成立， 因为 2 si 1 1 12 12cos 2 cos nc b sinAS c b cosA A AAB AC A         所以当 2cos 4A  时 S AB AC  取得最大值 7 2 ， 故答案为： 7 2 ． 【点睛】本题考查的是正余弦定理、三角形的面积公式、平面向量的数量积的定义及利用基 本不等式求最值，考查了学生的转化能力，属于中档题. - 14 - 三、解答题：共 70 分，解答应写出文字说明、证明过程或演算步骤．第 17-21 题为必考题， 每个试题考生都必须作答．第 22-23 题为选考题，考生根据要求作答．（一）必考题：共 60 分． 17.已知数列{an}的前 n 项和 Sn＝n2+pn，且 a4，a7，a12 成等比数列． （1）求数列{an}的通项公式； （2）若 bn 1 4 n n n S a a    ，求数列{bn}的前 n 项和 Tn． 【答案】（1）an＝2n+1，n∈N*．（2）Tn 22 2 2 3 n n n   ． 【解析】 【分析】 （1）根据公式 an 1 1 1 2,n n S n S S n n N        ， ， ，初步计算出数列{an}的含有参数 p 的通项公式， 然后将 a4，a7，a12 代入通项公式，并根据等比中项的性质列出关于 p 的方程，解出 p 的值，即 可得到数列{an}的通项公式. （2）根据第（1）题的结果计算出 Sn 的表达式，以及数列{bn}的通项公式，然后将通项公式进 行转化，最后运用裂项相消法可计算出前 n 项和 Tn． 【详解】解：（1）由题意，当 n＝1 时，a1＝S1＝1+p， 当 n≥2 时，an＝Sn﹣Sn﹣1＝n2+pn﹣（n﹣1）2﹣p（n﹣1）＝2n﹣1+p， ∵当 n＝1 时，a1＝1+p 也满足上式， ∴an＝2n﹣1+p， ∵a4，a7，a12 成等比数列，∴ 2 4 12 7a a a ， ∴ 2(7 )(23 ) (13 )p p p    ，解得 p＝2， ∴an＝2n+1，n∈N*． （2）由（1）知，Sn＝n2+2n， 则 1 4 n n n n Sb a a      24 8 2 1 2 3 n n n n    - 15 - 2 2 4 8 4 8 3 n n n n    2 2 4 8 3 3 4 8 3 n n n n      ＝1 2 3 4 8 3n n    ＝1    3 2 1 2 3n n    3 1 11 2 2 1 2 3n n        ， ∴Tn＝b1+b2+ +bn ＝[ 3 1 11 2 3 5      ]+[ 3 1 11 2 5 7      ]+ +[ 3 1 11 2 2 1 2 3n n       ] 3 1 1 1 1 1 1 2 3 5 5 7 2 1 2 3n n n             ＝n 3 2  （ 1 1 3 2 3n   ） 1 3 2 4 6n n     22 2 2 3 n n n   ． 【点睛】本题考查了由 Sn 求 na 、数列求和中的裂项求和法，属于中档题. 18.随着生活节奏的加快以及智能手机的普及，外卖点餐逐渐成为越来越多用户的餐饮消费习 惯，由此催生了一批外卖点餐平台．已知某外卖平台的送餐费用与送餐距离有关（该平台只 给 5 千米范围内配送），为调査送餐员的送餐收入，现从该平台随机抽取 100 名点外卖的用户 进行统计，按送餐距离分类统计结果如表： 送餐距离（千米） （0，1] （1，2] （2，3] （3，4] （4，5] 频数 15 25 25 20 15 - 16 - 以这 100 名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率． （1）若某送餐员一天送餐的总距离为 100 千米，试估计该送餐员一天的送餐份数；（四舍五 入精确到整数，且同一组中的数据用该组区间的中点值为代表）． （2）若该外卖平台给送餐员的送餐费用与送餐距离有关，规定 2 千米内为短距离，每份 3 元， 2 千米到 4 千米为中距离，每份 7 元，超过 4 千米为远距离，每份 12 元．记 X 为送餐员送一 份外卖的收入（单位：元），求 X 的分布列和数学期望． 【答案】（1）41 份（2）见解析，6.15 【解析】 【分析】 （1）利用频率分布表，计算每名外卖用户的平均送餐距离．然后求解送餐份数． （2）由题意知 X 的可能取值为：3，7，12，求出概率，得到分布列，然后求解期望即可． 【详解】解：（1）估计每名外卖用户的平均送餐距离为： 0.5×0.15+1.5×0.25+2.5×0.25+3.5×0.2+4.5×0.15＝2.45 千米． 所以送餐距离为 100 千米时，送餐份数为： 100 412.45  份； （2）由题意知 X 的可能取值为：3，7，12，   40 23 100 5P X    ，   45 97 100 20P X    ，   15 312 100 20P X    ， 所以 X 的分布列为： X 3 7 12 P 2 5 9 20 3 20 ∴   2 9 33 7 12 6.155 20 20E X        ． 【点睛】本题考查了离散型随机变量的分布列、数学期望，考查了考生的分析能力，属于中 档题. 19.如图，在四棱锥 P﹣ABCD 中，底面 ABCD 是边长为 2 的菱形，∠DAB＝60°，AD⊥PD，点 F 为棱 PD 的中点． - 17 - （1）在棱 BC 上是否存在一点 E，使得 CF∥平面 PAE，并说明理由； （2）若 AC⊥PB，二面角 D﹣FC﹣B 的余弦值为 6 6 时，求直线 AF 与平面 BCF 所成的角的正弦 值． 【答案】（1）存在，见解析（2） 5 5 ． 【解析】 【分析】 （1）取点 E 为棱 BC 的中点，取 PA 的中点 Q，连结 EQ、FQ，利用已知结合三角形中位线定理 可证四边形 CEQF 为平行四边形，得到 CF∥EQ，再由直线与平面平行的判定得 CF∥平面 PAE； （2）取 AB 中点 M，以 D 为坐标原点，分别以 DM，DC，DP 所在直线为 x，y，z 轴建立空间直 角坐标系.设 FD＝a，利用平面 FBC 与平面 DFC 的所成角的余弦值求得 a，可得平面 BCF 的一 个法向量及 FA  的坐标再由两向量所成角的余弦值可得 FA 与平面 BCF 所成的角的正弦值. 【详解】（1）在棱 BC 上存在点 E，使得 CF∥平面 PAE，点 E 为棱 BC 的中点. 证明：取 PA 的中点 Q，连结 EQ、FQ， 由题意，FQ∥AD 且 1 2FQ AD ，CE∥AD 且 1 2CE AD ， 故 CE∥FQ 且 CE＝FQ. ∴四边形 CEQF 为平行四边形. ∴CF∥EQ，又CF  平面 PAE， EQ 在平面 PAE 内， ∴CF∥平面 PAE； （2）取 AB 中点 M， 以 D 为坐标原点，分别以 DM，DC，DP 所在直线为 x，y，z 轴建立空间直角坐标系. 设 FD＝a，则 D（0，0，0），F（0，0，a），C（0，2，0）， - 18 - B（ 3 ，1，0），A（ 3 1 0， ，）.  0 2FC a  ，， ，  3 1 0CB   ， ， . 设平面 FBC 的一个法向量为  m x y z ， ， . 由 2 0 3 0 m FC y az m CB x y            ，取 x＝1，得 2 31 3m a        ， ， ； 取平面 DFC 的一个法向量为  1 0 0n  ，， . 由题意， 2 6 1 6 121 3 cos m n a      ＜ ， ＞ ，解得 a 6 . ∴  3 1 6FA    ， ， . 设直线 AF 与平面 BCF 所成的角为θ， 则sin cos m FA  ＜ ， ＞ 2 3 5 56 10 m FA m FA        . 即直线 AF 与平面 BCF 所成的角的正弦值为 5 5 . 【点睛】 本题主要考查了线面平行的证明，利用向量法解决直线与平面所成角的问题，属于中档题. 20.已知椭圆   2 2 2 2 1 0x yC a ba b  ： ＞ ＞ ，四点  1 2 3P ， ，  2 0 2P ， ， 3 62 3P      ， ， 4 62 3P       ， 中恰有三个点在椭圆 C 上，左、右焦点分别为 F1、F2． （1）求椭圆 C 的方程； - 19 - （2）过左焦点 F1 且不平行坐标轴的直线 l 交椭圆于 P、Q 两点，若 PQ 的中点为 N，O 为原点， 直线 ON 交直线 x＝﹣3 于点 M，求 1 PQ MF 的最大值． 【答案】（1） 2 2 16 2 x y  ；（2） 3 ． 【解析】 【分析】 （1）由椭圆的对称性可得 P2，P3，P4 在椭圆上，进而求出椭圆的方程； （2）由（1）可得 F1 的坐标，由题意设直线 l 的方程与椭圆联立，求出两根之和及两根之积， 求出 PQ 的中点 N 的坐标，再由直线 ON 与 x＝﹣3，求出 M 的坐标，进而求出 1 PQ MF 的表达式， 换元由二次函数配方可得其最大值． 【详解】解：（1）由椭圆的对称性易知 3 62 3P      ， ， 4 62 3P       ， 关于 y 轴对称， 一定都在椭圆上．所以  1 2 3P ， 一定不在椭圆上． 根据题意  2 0 2P ， 也在椭圆上， 将  2 0 2P ， ， 4 62 3P       ， 带入椭圆方程，解得椭圆方程为 2 2 16 2 x y  ； （2）设直线 l 方程为 y＝k（x+2）（k≠0），P（x1，y1），Q（x2，y2）， 联立   2 2 16 2 2 x y y k x       ，可得（3k2+1）x2+12k2x+12k2﹣6＝0； 则  ＝24（k2+1）＞0，且 2 1 2 2 12 3 1 kx x k     ， 2 1 2 2 12 6 3 1 kx x k   ， 设 PQ 的中点 N（x0，y0），则 2 1 2 0 2 6 2 3 1 x x kx k     ， 2 0 2 2 6 223 1 3 1 k ky k k k         ， ∴N 坐标为 2 2 2 6 2 3 1 3 1 k k k k      ， ，  22 2 2 2 2 6 12 6 11 3 1 3 1 kkPQ k k k     ，； - 20 - 因此直线 ON 的方程为 1 3y xk   ，从而点 M 为 13 k     ， ，又 F1（﹣2，0）， 所以     2 22 22 21 24 1| | | | 3 1 k kPQ MF k    ，令 u＝3k2+1≥1， 则      2 2 2 1 2 16 1 1 1 16 1 1 98 [ )3 3 2 2 3 4 16 u uh u u u u u                     ， 因此当 u＝4，即 k＝±1 时 h（u）最大值为3． 所以 1 PQ MF 取得最大值 3 ． 【点睛】本题考查了待定系数法求椭圆的标准方程、直线与椭圆的位置关系中的最值问题， 考查了考生的计算能力，属于难题. 21.已知函数   bxef x ax  在 2x  处取到极值为 2 e ． （1）求函数  f x 的单调区间； （2）若不等式  2 ln 1x f x kx x   在  0,x  上恒成立，求实数 k 的取值范围． 【答案】（1）单调递减区间是   ,0 , 0,2 ，单调递增区间是 2, ；（2） 1 2     ， ． 【解析】 【分析】 （1）求出函数的导数，结合题意得到关于 a，b 的方程，求出 a，b 的值，求出函数的单调区 间即可； （2）问题等价于 2 1x lnxe kx   在  0,x  上恒成立，令    2 1 0 x lnxg x e xx   ＞ ，则 只需  mink g x 即可，根据函数的单调性判断求解即可． 【详解】解：（1）由已知定义域为   ,0 0,  ，      2 bxabx a ef x ax   ， - 21 - 由       2 2 22 0 2 bab a ef a    ，又 0a  ，得 1 2b  ，   2 2 2 2 2 be e ef a a    ，所以 1a  ， 所以   2 2 12 xx e f x x      ，又 0x  ． 由   0f x  得：x＞2；由   0f x  得：x＜0 或 0＜x＜2． 故 f（x）的单调递减区间是   ,0 , 0,2 ；单调递增区间是  2, . （2）问题等价于 2 1x lnxe kx   在 x∈ 0, 上恒成立， 令    2 1 0 x lnxg x e xx   ＞ ， 则只需  mink g x 即可．   2 2 2 1 2 x x e lnx g x x   ， 令    2 21 02 x h x x e lnx x  ＞ ， 则   2 21 1 04 x h x x x e x        ＞ ． 所以  h x 在  0,x  上单调递增， 又 41 2 02 8 eh ln      ＜ ，  1 02 eh  ＞ ， 所以有唯一的零点 0 1 12x     ， ，  g x 在 0 1 ,2x x    上单调递减，在  0 ,1x x 上单调递增． - 22 - 因为 02 0 2 0 02 xx e lnx  ，两边同时取自然对数，则有  0 0 0 02 2 x xln lnx ln lnx    ， 即  0 0 0 02 2 x xln lnx ln lnx     ． 构造函数    ln 0m x x x x   ，则   11 0m x x   ＞ ， 所以函数  m x 在  0,x  上单调递增， 又  0 02 xm m lnx      ，所以 0 02 x lnx  ，即 0 2 0 1x e x  ． 所以     0 0 02 0 0 0 0 11 1 12 2 x x lnxg x g x e x x x        ，即   1 2ming x  ， 于是实数 k 的取值范围是 1 2     ， ． 【点睛】考查求含参数的函数的单调性以及不等式恒成立求参数的取值范围，后一个问题一 般是分离参数，转化为求函数的最值，不过构造函数是难点；本题是难题. （二）选考题：共 10 分，请考生在 22、23 题中任选一题作答，如果多做则按所做的第一题 计分 [选修 4-4 坐标系与参数方程] 22.在直角坐标系 xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线 C1 的极 坐标方程为ρsinθ＝2． （1）M 为曲线 C1 上的动点，点 P 在线段 OM 上，且满足 4PO OM    ，求点 P 的轨迹 C2 的直 角坐标方程； （2）曲线 C2 上两点 1 3A      ， 与点 B（ρ2，α），求△OAB 面积的最大值． 【答案】（1）x2+（y﹣1）2＝1（y≠0）．（2） 3 3 4 ． 【解析】 【分析】 （1 ）设出 P 的极坐标，然后由题意得出极坐标方程，最后转化为直角坐标方程为 - 23 - 2 2( 1) 1( 0)x y y    ; （2）利用（1）中的结论，设出点的极坐标，然后结合面积公式得到面积的三角函数，结合 三角函数的性质可得 OAB 面积的最大值为 3 3 4 . 【详解】解：（1）设 P 的极坐标为（ρ，θ）（ρ＞0），M 的极坐标为（ρ0，θ）（ρ0＞0）． 由题设知|PO|＝ρ， 0 2OM sin    ． 由 PO OM PO OM cos PO OM           4， 得 2 4sin    ， 所以 C2 的极坐标方程ρ＝2sinθ（ρ＞0）， 因此 C2 的直角坐标方程为 x2+（y﹣1）2＝1（y≠0）． （2）依题意： 1 2 33OA sin    ，|OB|＝ρ2＝2sinα． 于是△OAB 面积：S 1 3 13 22 3 2 6 2OA OB sin AOB sin sin sin                   ． 当 2 3   时，S 取得最大值 3 3 4 ． 所以△OAB 面积的最大值为 3 3 4 ． 【点睛】本题考查了极坐标方程的求法及应用，重点考查了转化与化归能力.在求曲线交点、 距离、线段长等几何问题时，求解的一般方法是将其化为普通方程和直角坐标方程后求解， 或者直接利用极坐标的几何意义求解.要结合题目本身特点，确定选择何种方程. [选修 4-5：不等式选讲] 23.已知 a，b，c 均为正数，设函数 f（x）＝|x﹣b|﹣|x+c|+a，x∈R． （1）若 a＝2b＝2c＝2，求不等式 f（x）＜3 的解集； （2）若函数 f（x）的最大值为 1，证明： 1 4 9 36a b c    ． 【答案】（1） 1 2       ， ．（2）见解析 【解析】 【分析】 - 24 - （1）根据 a＝2b＝2c＝2 时，将不等式 f（x）＜3 化为|x﹣1|﹣|x+1|＜1，然后利用零点分 段法解不等式即可； （2）根据条件利用绝对值三角不等式，可得 a+b+c＝1，然后利用柯西不等式，即可证明 1 4 9 36a b c    ． 【详解】（1）当 a＝2b＝2c＝2 时，a＝2，b＝c＝1 不等式 f（x）＜3 化为|x﹣1|﹣|x+1|＜1， 当 x≤﹣1 时，原不等式化为 1﹣x+1+x＜1，解集为∅ ； 当﹣1＜x＜1 时，原不等式化为 1﹣x﹣x﹣1＜1，解得 1 12 x ＜ ＜ ； 当 x≥1 时，原不等式化为 x﹣1﹣x﹣1＜1，解得 x≥1， ∴不等式 f（x）＜3 的解集为 1 2       ， ． （2）∵      f x x b x c a x b x c a b c a             又∵a，b，c＞0， ∴  max =1f x a b c   ∴         2 2 2 2 2 21 4 9 1 2 3a b c a b ca b c a b c                                       21 2 3( )a b c a b c       =36 当且仅当 1 2 3 2 a b c a b c        ，即 1 2 13 3a b c  ， ， 时等号成立， ∴ 1 4 9 36a b c    ． 【点睛】本题主要考查绝对值不等式的求解，柯西不等式的应用，属于中档题. - 25 -