- 2021-07-01 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年湖北省黄冈中学高考数学三模试卷(文科)
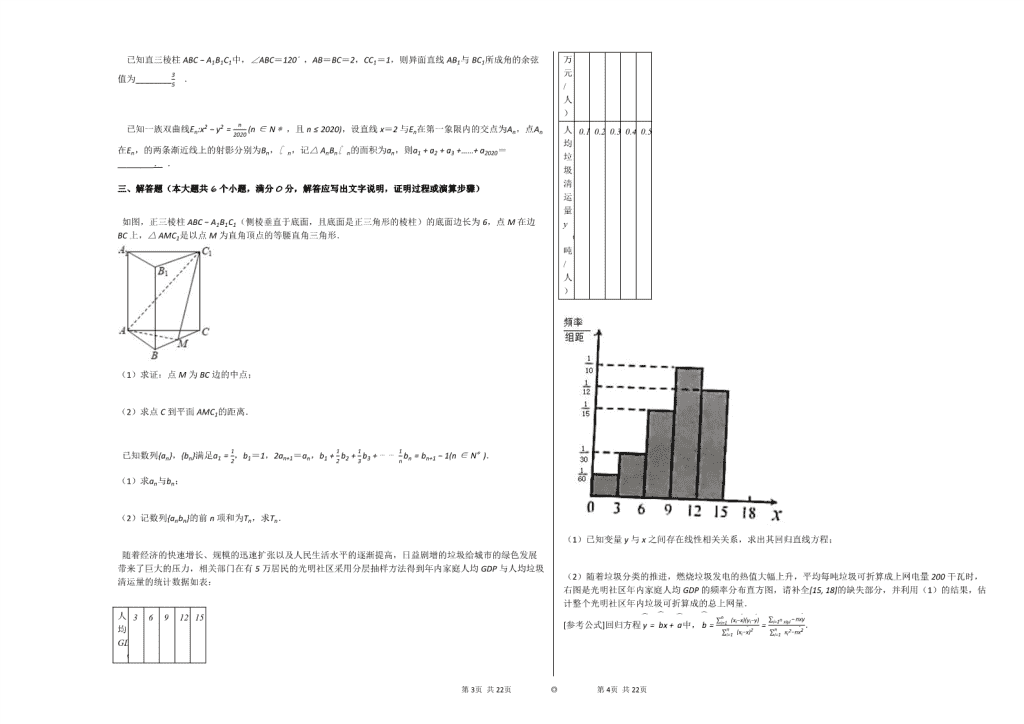
2020年湖北省黄冈中学高考数学三模试卷(文科) 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1. 已知集合A={−1, 0, 1, 3, 5},B={x|x>3或x<1},则(∁RB)∩A=( ) A.{−1, 0, 5} B.{1, 2, 3} C.{2, 3} D.{1, 3} 2. 复数z=3+i1−2i(其中i为虚数单位),则|z¯|=( ) A.2 B.43 C.2 D.5 3. 已知直线l1:mx+y−1=0,l2:(2m+3)x+my−1=0,m∈R,则“m=−2”是“l1⊥l2”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 4. 如图所示,在边长为4的正三角形中有一封闭曲线围成的阴影区域.在正三角形中随机撒一粒豆子,它落在阴影区域内的概率为34,则阴影区域的面积为( ) A.3 B.23 C.33 D.43 5. 设x,y满足约束条件x+3y≥3x−y≥1y≥0 ,则z=x+y的最小值为( ) A.0 B.1 C.2 D.3 6. 在△ABC中AC→=5AD→,E是直线BD上一点,且BE→=2BD→,若AE→=mAB→+nAC→,则m+n=( ) A.25 B.−25 C.35 D.−35 7. 中国气象局规定:24小时内降雨的深度称为日降雨量,表示降雨量的单位通常用毫米.例如:1毫米的降雨量是指单位面积上水深1毫米.在连续几天的暴雨天气中,某同学用一个长方体容器来测量降雨量,已知该长方体的底面是边长为20mm的正方形,高为40mm,该容器的容器口为上底面正方形的内切圆,将该容器放在雨中,雨水从圆形容器口进入容器中,24小时后,测得容器中水深10mm,则该同学测得的降水量约为( )(π取3.14) A.127毫米 B.12.7毫米 C.509毫米 D.100毫米 8. 已知圆C:x2+(y+2)2=2,则在x轴和y轴上的截距相等且与圆C相切的直线有几条( ) A.3条 B.2条 C.1条 D.4条 9. 若函数f(x)=3sinx+cosx在区间[a, b]上是增函数,且f(a)=−2,f(b)=2,则函数g(x)=3cosx−sinx在区间[a, b]上( ) A.是增函数 B.是减函数 C.可以取得最大值2 D.可以取得最小值−2 10. 棱长为1的正方体ABCD−A1B1C1D1中P为正方体表面上的一个动点,且总有PC⊥BD1,则动点P的轨迹的长度为( ) A.34π B.4π C.32 D.42 11. 已知F1(−c, 0)、F2(c, 0)是双曲线C:x2a2−y2b2=1的左、右焦点,F1关于双曲线的一条渐近线的对称点为P,且点P在抛物线y2=4cx上,则双曲线的离心率为( ) A.2+1 B.2 C.5 D.5+12 12. 已知等腰三角形一腰上的中线长为2,则该三角形面积的最大值是( ) A.433 B.83 C.423 D.9 二、填空题(本大题共4小题,每小题5分,共20分) 若lna=1e,则ae−logae=________. 设x=θ是函数f(x)=3sinx−cosx的一个极值点,则sin2θ+2cos2θ=________. 第21页 共22页 ◎ 第22页 共22页 已知直三棱柱ABC−A1B1C1中,∠ABC=120∘,AB=BC=2,CC1=1,则异面直线AB1与BC1所成角的余弦值为________35 . 已知一族双曲线En:x2−y2=n2020(n∈N*,且n≤2020),设直线x=2与En在第一象限内的交点为An,点An在En,的两条渐近线上的射影分别为Bn,∁n,记△AnBn∁n的面积为an,则a1+a2+a3+……+a2020= ________. . 三、解答题(本大题共6个小题,满分0分,解答应写出文字说明,证明过程或演算步骤) 如图,正三棱柱ABC−A1B1C1(侧棱垂直于底面,且底面是正三角形的棱柱)的底面边长为6,点M在边BC上,△AMC1是以点M为直角顶点的等腰直角三角形. (1)求证:点M为BC边的中点; (2)求点C到平面AMC1的距离. 已知数列{an},{bn}满足a1=12,b1=1,2an+1=an,b1+12b2+13b3+⋯⋯1nbn=bn+1−1(n∈N*). (1)求an与bn; (2)记数列{anbn}的前n项和为Tn,求Tn. 随着经济的快速增长、规模的迅速扩张以及人民生活水平的逐渐提高,日益剧增的垃圾给城市的绿色发展带来了巨大的压力,相关部门在有5万居民的光明社区采用分层抽样方法得到年内家庭人均GDP与人均垃圾清运量的统计数据如表: 人均GDPx(万元/人) 3 6 9 12 15 人均垃圾清运量y(吨/人) 0.13 0.23 0.31 0.41 0.52 (1)已知变量y与x之间存在线性相关关系,求出其回归直线方程; (2)随着垃圾分类的推进,燃烧垃圾发电的热值大幅上升,平均每吨垃圾可折算成上网电量200干瓦时,右图是光明社区年内家庭人均GDP的频率分布直方图,请补全[15, 18]的缺失部分,并利用(1)的结果,估计整个光明社区年内垃圾可折算成的总上网量. [参考公式]回归方程y=bx+a中,b=i=1n (xi−x¯)(yi−y¯)i=1n (xi−x¯)2=i=1n xiyi−nxy¯i=1n xi2−nx¯2. 已知点F1,F2是椭圆C:x2a2+y2b2=1(a>b>0))的左、右焦点,椭圆上一点P满足PF1⊥x轴,|PF2|=5|PF1|,|F1F2|=22. (1)求椭圆C的标准方程; (2)过F2的直线l交椭圆C于A,B两点,当△ABF1的内切圆面积最大时,求直线l的方程. 已知函数f(x)=2(x−1)x+a−lnx,其中a>0. (1)求f(x)的单调区间; (2)设x1,x2是f(x)的两个极值点,判断1f(x1)+1f(x2)的正负,并说明理由. [选修4-4:坐标系与参数方程] 第21页 共22页 ◎ 第22页 共22页 在平面直角坐标系中,已知曲线C1:x=23+10cosαy=10sinα (α为参数),P(3,3).以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l1的极坐标方程为θ=π6(ρ∈R). (1)求曲线C1的极坐标方程及点P的极坐标; (2)设直线l1与曲线C1交于A、B两点,记△POA的面积为S,△BOC1的面积为S′,求SS′+S′S的值. [选修4-5:不等式选讲] 已知函数f(x)=m−|x−2|,m∈R,且f(x+2)≥1的解集A满足[−1, 1]⊆A. (1)求实数m的取值范围B; (2)若a,b,c∈(0, +∞),m0为B中的最小元素且1a+12b+13c=m0,求证:a+2b+3c≥92. 第21页 共22页 ◎ 第22页 共22页 参考答案与试题解析 2020年湖北省黄冈中学高考数学三模试卷(文科) 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1. 【答案】 D 【考点】 交、并、补集的混合运算 【解析】 根据补集和交集的定义,计算即可. 【解答】 集合A={−1, 0, 1, 3, 5},B={x|x>3或x<1}, 则∁RB={x|1≤x≤3}, 所以(∁RB)∩A={1, 3}. 2. 【答案】 C 【考点】 复数的模 【解析】 根据|z¯|=|z|,计算即可. 【解答】 设复数z=3+i1−2i, 则|z¯|=|z|=|3+i1−2i|=|3+i||1−2i| =32+1212+(−2)2=105=2. 3. 【答案】 A 【考点】 充分条件、必要条件、充要条件 【解析】 由两直线垂直与系数的关系列式求得m值,可得“m=−2”⇒“l1⊥l2”,反之不成立.再由充分必要条件的判定方法得答案. 【解答】 直线l1:mx+y−1=0,l2:(2m+3)x+my−1=0,m∈R, l1⊥l2⇔m(2m+3)+m=0,即m=−2或m=0. ∴ 由“m=−2”⇒“l1⊥l2”,反之不成立. ∴ “m=−2”是“l1⊥l2”的充分不必要条件. 4. 【答案】 C 【考点】 几何概型计算(与长度、角度、面积、体积有关的几何概型) 【解析】 由题意结合几何概型计算公式得到关于面积的方程,解方程即可求得最终结果. 【解答】 设阴影部分的面积为S,结合几何概型公式可得:S12×4×4×32=34; 解得S=33: 5. 【答案】 C 【考点】 简单线性规划 【解析】 作出不等式组表示的平面区域,由z=x+y可得y=−x+z,则z表示直线y=−x+z在y轴上的截距,截距越小,z越小,结合图象可求z的最小值. 【解答】 作出不等式组表示的平面区域,如图所示的阴影部分: 由z=x+y可得y=−x+z,则z表示直线y=−x+z在y轴上的截距,截距越小,z越小, 由题意可得,x+3y=3x−y=1 ,解得A(32, 12), 当y=−x+z经过点A时,z最小, 由可得A(32, 12),此时z=x+y=2. 6. 【答案】 【考点】 平面向量的基本定理 【解析】 根据题意,画出图象,可知AE→=AB→+BE→=AB→+2BD→=AB→+2(AD→−AB→)=AB→+2(15AC→−AB→)=−AB→+25AC→.进而求得m和n的值,算出m+n的值. 【解答】 如图所示: 第21页 共22页 ◎ 第22页 共22页 AE→=AB→+BE→=AB→+2BD→=AB→+2(AD→−AB→)=AB→+2(15AC→−AB→)=−AB→+25AC→. ∵ AE→=mAB→+nAC→, ∴ m=−1,n=25. m+n=−35. 故选:D. 7. 【答案】 B 【考点】 棱柱、棱锥、棱台的体积 【解析】 由题意求出容器中水的容积,除以圆的面积得答案. 【解答】 由题意,水的体积V=20×20×10=4000mm3, 容器口的面积S=π×102=100πmm2, ∴ 降雨量=4000100π≈12.7mm. ∴ 该同学测得的降水量约为12.7毫米. 8. 【答案】 A 【考点】 直线与圆的位置关系 【解析】 先看直线不过原点的情况,设出直线的方程,斜率为−1,则可知这样的直线有2条,再看直线过原点的情况,把原点代入即可知原点在圆外,则这样的直线也应该有2条,最后验证以上4条中有一条是重复,最后综合得到结论. 【解答】 若直线不过原点,其斜率=−1,设其方程为y=−x+m, 则d=|0−2−m|2=2,解得m=0或−4,当m=0时,直线过原点; 若过原点,把(0, 0)代入02+(0+2)2=4>2, 即原点在圆外,所以过原点有2条切线, 综上,一共有3条, 9. 【答案】 C 【考点】 正弦函数的图象 函数单调性的性质与判断 【解析】 由题意利用两角和差的三角公式化简函数的解析式,再利用正弦函数的图象和性质,得出结论. 【解答】 ∵ 函数f(x)=3sinx+cosx=2sin(x+π6) 在区间[a, b]上是增函数, 且f(a)=−2,f(b)=2, ∴ f(a)=2sin(a+π6)为最小值,f(b)=2sin(b+π6)为最大值, 则函数g(x)=3cosx−sinx=2cos(x+π6)=2sin(x+π6+π2), 即g(x)的图象由f(x)的图象向左平移π2个单位(即14个周期)得到的. 令x+π6=t,取t∈[−π2, π2],则t+π2∈[0, π], 故g(x)在区间[a, b]上能取得最大值2, 10. 【答案】 C 【考点】 轨迹方程 空间中直线与直线之间的位置关系 【解析】 画出正方体,利用已知条件,判断P的轨迹,然后求解轨迹长度. 【解答】 P点的轨迹为过点C与直线BD1垂直的截面与正方体的交线,就是图形中点三角形ACB1,它的周长为:32. 11. 【答案】 D 【考点】 双曲线的离心率 圆锥曲线的综合问题 【解析】 利用已知条件画出图形,求出P的坐标,代入抛物线方程,然后转化求解双曲线的离心率即可. 【解答】 如图:F1P垂直直线bx−ay=0,交点为H,F1到双曲线的一条渐近线bx−ay=0的距离为:d=bca2+b2=b, △F1PF2中,PF1=2d=2b,抛物线y2 第21页 共22页 ◎ 第22页 共22页 =4cx的焦点坐标(c, 0), PF2=2a,tan∠F1OH=ba,∴ cos∠F1OH=ac,sin∠F1OH=bc, 可得cos∠OF1P=bc,sin∠OF1P=ac,P(2b2c−c, 2abc), 点P在抛物线y2=4cx上, 可得:4a2b2c2=4c⋅(2b2c−c)=8b2−4c2, ∴ e4−3e2+1=0,e>1, ∴ e=5+12. 12. 【答案】 B 【考点】 解三角形 【解析】 结合已知三角形考虑建立直角坐标系,结合点的坐标表示三角形的面积,然后结合基本不等式即可求解. 【解答】 建立如图所示的直角坐标系,设C(m, 0)则B(−m, 0),A (0, n),D(12m,12n), 由题意可得BD2=(3m2)2+(n2)2=4, 故S=mn=43⋅3m2⋅n2≤43⋅(3m2)2+(n2)22=83, 当且仅当3m2=n2即n=3m时取等号 二、填空题(本大题共4小题,每小题5分,共20分) 【答案】 0 【考点】 对数的运算性质 【解析】 由已知结合指数与对数的相互转化及对数的运算性质即可求解. 【解答】 因为lna=1e, 所以a=e1e, 则ae−logae=ee×1e−1lna=e−e=0 【答案】 −25 【考点】 利用导数研究函数的极值 同角三角函数间的基本关系 【解析】 根据极值点处的导数为零,求出tanθ的值,然后再借助于三角恒等变换求出结论. 【解答】 f′(x)=3cosx+sinx, ∴ f′(θ)=3cosθ+sinθ=0,∴ tanθ=−3. ∴ sin2θ+2cos2θ=2sinθcosθ+2cos2θcos2θ+sin2θ=2tanθ+21+tan2θ=−25. 【答案】 35 【考点】 异面直线及其所成的角 【解析】 连接B1C,交BC1于点O,取AC的中点D,连接BD、OD,则OD // AB1,故∠BOD即为所求;得出BD、OD和OB的长度后,由余弦定理求得cos∠BOD即可. 【解答】 连接B1C,交BC1于点O,则点O为B1C的中点,取AC的中点D,连接BD、OD, ∴ OD // AB1,∴ ∠BOD即为异面直线AB1与BC1所成角. ∵ ∠ABC=120∘,AB=BC=2,CC1=1, ∴ BD=1,OD=12AB1=52,OB=12BC1=52, 在△BOD中,由余弦定理知,cos∠BOD=OB2+OD2−BD22⋅OB⋅OD=54+54−12×52×52=35. 【答案】 20218 【考点】 双曲线的离心率 数列的求和 【解析】 一族双曲线由有共同的渐近线且互相垂直,可得△AnBn∁n为直角三角形,通过计算可求出An的坐标,|AnBn|和|An∁n|,进而求出an和a1+a2+a3+……+a2020. 【解答】 双曲线En:x2−y2=n2020(n∈N*,且n≤2020)的两条渐近线为y=x,y=−x,互相垂直, 直线x=2与En在第一象限内的交点为An,An(2,4−n2020), 点An在En的两条渐近线上的射影分别为Bn,∁n 第21页 共22页 ◎ 第22页 共22页 ,则|AnBn|=2−4−n20202,|AnCn|=2+4−n20202, ∴ an=12|AnBn||AnCn|=n20204=n8080, ∴ a1+a2+a3+⋯⋯+a2020=18080+28080+⋯⋯+20208080=1+20202×20208080=20218. 三、解答题(本大题共6个小题,满分0分,解答应写出文字说明,证明过程或演算步骤) 【答案】 证明:∵ △AMC1为以点M为直角顶点的等腰直角三角形, ∴ AM⊥C1M且AM=C1M ∵ 三棱柱ABC−A1B1C1,∴ CC1⊥底面ABC ∴ C1M在底面内射影为CM,∴ AM⊥CM. ∵ 底面ABC为正三角形,∴ 点M为BC边的中点 过点C作CH⊥MC1,由(1)知AM⊥C1M且AM⊥CM, ∴ AM⊥平面C1CM, ∵ CH在平面C1CM内,∴ CH⊥AM, ∴ CH⊥平面C1AM 由(1)知,AM=C1M=33,CM=12BC=3,CC1⊥BC, ∴ CC1=(33)2−32=32, ∴ CH=CC1×CMC1M=32×333=6, ∴ 点C到平面AMC1的距离为底面边长为6. 【考点】 点、线、面间的距离计算 【解析】 (1)根据等腰直角三角形,可得AM⊥C1M且AM=C1M,根据三垂线定理可知AM⊥CM,而底面ABC为边长为a的正三角形,进一步得到点M为BC边的中点; (2)过点C作CH⊥MC1,根据线面垂直的判定定理可知AM⊥平面C1CM,CH⊥平面C1AM,则CH即为点C到平面AMC1的距离,根据等面积法可求出CH的长. 【解答】 证明:∵ △AMC1为以点M为直角顶点的等腰直角三角形, ∴ AM⊥C1M且AM=C1M ∵ 三棱柱ABC−A1B1C1,∴ CC1⊥底面ABC ∴ C1M在底面内射影为CM,∴ AM⊥CM. ∵ 底面ABC为正三角形,∴ 点M为BC边的中点 过点C作CH⊥MC1,由(1)知AM⊥C1M且AM⊥CM, ∴ AM⊥平面C1CM, ∵ CH在平面C1CM内,∴ CH⊥AM, ∴ CH⊥平面C1AM 由(1)知,AM=C1M=33,CM=12BC=3,CC1⊥BC, ∴ CC1=(33)2−32=32, ∴ CH=CC1×CMC1M=32×333=6, ∴ 点C到平面AMC1的距离为底面边长为6. 【答案】 数列{an}满足a1=12,b1=1,2an+1=an, 所以an+1an=12(常数), 所以数列{an}是以12为首项12为公比的等比数列. 所以an=12×12n−1=12n. 数列{bn}满足b1+12b2+13b3+⋯+1nbn=bn+1−1(n∈N*)① 当n≥2时,b1+12b2+13b3+⋯+1n−1bn−1=bn−1(n∈N*)②, ①-②得1nbn=bn+1−bn, 所以bn+1bn=n+1n, 所以b2b1⋅b3b2⋯bnbn−1=2×32×43×⋯n−1n−2×nn−1, 整理得bnb1=n, 所以bn=n(首项符合通项) 故bn=n. 第21页 共22页 ◎ 第22页 共22页 由(1)得:cn=anbn=n⋅12n, 所以Tn=1×12+2×122+⋯+n⋅12n①. 12Tn=1×122+2×123+⋯+n⋅12n+1②, ①-②得:12Tn=(12+122+⋯+12n)−n⋅12n+1=12(1−12n)1−12−n⋅12n+1=1−12n−n⋅12n+1. 故Tn=2−12n−1−n2n. 【考点】 数列递推式 数列的求和 【解析】 (1)直接利用数列的递推关系式和叠乘法的应用求出数列的通项公式. (2)利用(1)的结论,进一步利用乘公比错位相减法求出数列的和. 【解答】 数列{an}满足a1=12,b1=1,2an+1=an, 所以an+1an=12(常数), 所以数列{an}是以12为首项12为公比的等比数列. 所以an=12×12n−1=12n. 数列{bn}满足b1+12b2+13b3+⋯+1nbn=bn+1−1(n∈N*)① 当n≥2时,b1+12b2+13b3+⋯+1n−1bn−1=bn−1(n∈N*)②, ①-②得1nbn=bn+1−bn, 所以bn+1bn=n+1n, 所以b2b1⋅b3b2⋯bnbn−1=2×32×43×⋯n−1n−2×nn−1, 整理得bnb1=n, 所以bn=n(首项符合通项) 故bn=n. 由(1)得:cn=anbn=n⋅12n, 所以Tn=1×12+2×122+⋯+n⋅12n①. 12Tn=1×122+2×123+⋯+n⋅12n+1②, ①-②得:12Tn=(12+122+⋯+12n)−n⋅12n+1=12(1−12n)1−12−n⋅12n+1=1−12n−n⋅12n+1. 故Tn=2−12n−1−n2n. 【答案】 由表格可得,x¯=5×(3+15)2×5=9, y¯=0.13+0.23+0.31+0.41+0.525=0.32, i=15 (xi−x¯)2=36+9+0+9+36=90, i=15 (xi−x¯)(yi−y¯)=(−6)×(−0.19)+(−3)×(−0.09)+0×(−0.01)+3×0.09+6×0.2 =6×(0.19+0.09+0.20)=6×0.48=2.88, 所以b=i=15 (xi−x¯)(yi−y¯)i=15 (xi−x¯)2=2.8890=0.032, 于是a=y¯−bx¯=0.32−0.032×9=0.032, 故变量y与x之间的回归直线方程为y=0.032(x+1). 由频率分布直方图各小矩形的面积之和为1,得160×(1+2+4+6+5+a)×3=1, 解得a=2,故最右边小矩形的高度为260=130, 由频率分布直方图可知,光明社区的人均GDP为 x¯=360(1×1.5+2×4.5+4×7.5+6×10.5+5×13.5+2×16.5)=10.2(万元/人), 由(1)可知,光明社区的人均垃圾清运量约为0.032×(10.2+1)(吨/人). 于是光明社区年内垃圾清运总量为5×0.032×(10.2+1)=1.792(万吨). 由题意,整个光明社区年内垃圾可折算成的总上网量估计为: 17920×200=3.584×106(千瓦时)即为所求. 【考点】 求解线性回归方程 【解析】 (1)由最小二乘法,算出b,a,进而可得回归直线方程. (2)由频率分布直方图各小矩形的面积之和为1,得a=2,最右边小矩形的高度,人均GDP,进而得光明社区的人均垃圾清运量约为0.032×(10.2+1)(吨/人).于是光明社区年内垃圾清运总量,进而得出答案. 【解答】 由表格可得,x¯=5×(3+15)2×5=9, y¯=0.13+0.23+0.31+0.41+0.525=0.32, i=15 (xi−x¯)2=36+9+0+9+36=90, i=15 (xi−x¯)(yi−y¯)=(−6)×(−0.19)+(−3)×(−0.09)+0×(−0.01)+3×0.09+6×0.2 =6×(0.19+0.09+0.20)=6×0.48=2.88, 所以b=i=15 (xi−x¯)(yi−y¯)i=15 (xi−x¯)2=2.8890=0.032, 于是a=y¯−bx¯=0.32−0.032×9=0.032, 故变量y与 第21页 共22页 ◎ 第22页 共22页 x之间的回归直线方程为y=0.032(x+1). 由频率分布直方图各小矩形的面积之和为1,得160×(1+2+4+6+5+a)×3=1, 解得a=2,故最右边小矩形的高度为260=130, 由频率分布直方图可知,光明社区的人均GDP为 x¯=360(1×1.5+2×4.5+4×7.5+6×10.5+5×13.5+2×16.5)=10.2(万元/人), 由(1)可知,光明社区的人均垃圾清运量约为0.032×(10.2+1)(吨/人). 于是光明社区年内垃圾清运总量为5×0.032×(10.2+1)=1.792(万吨). 由题意,整个光明社区年内垃圾可折算成的总上网量估计为: 17920×200=3.584×106(千瓦时)即为所求. 【答案】 由题意可得|PF2|=5|PF1|,|F1F2|=22, |PF1|2+|F1F2|2=|PF2|2,解得|PF2|=533,|PF1|=33, 由椭圆的定义可得2a=533+33=23,所以a=3,c=2,b=1, 所以椭圆的方程为x23+y2=1; 要使△ABF1的内切圆面积最大,只需△ABF1的内切圆的半径r最大. 因为F1(−2, 0),F2(2, 0),设A(x1, y1),B(x2, y2), 显然直线l的斜率不为0,设直线l:x=ty+2,联立x=ty+2x2+3y2=3 , 可得(3+t2)y2+22ty−1=0,则y1+y2=−22t3+t2,y1y2=−13+t2, 则S△ABF1=S△F1F2A+S△F1F2B=12|F1F2|⋅|y1−y2|=2⋅(y1+y2)2−4y1y2 =2⋅(−22t3+t2)2+43+t2=26t2+13+t2, 又S△ABF1=12(|AF1|+|BF1|+|AB|)⋅r=12⋅43⋅r=23r, 故26t2+13+t2=23r,即r=2t2+13+t2=2t2+1+2t2+1≤12, 当且仅当t2+1=2t2+1,即t=±1时等号成立. 所以直线l的方程为y=x−2或y=−x+2. 【考点】 椭圆的标准方程 椭圆的应用 直线与椭圆的位置关系 【解析】 (1)由条件和勾股定理、椭圆的定义,解方程可得a,b,然后求出椭圆的方程; (2)设直线l:x=ty+2,△ABF1的内切圆的半径为r,由等积法可得r关于t的函数,利用基本不等式计算r的最大值,进而得到直线的方程. 【解答】 由题意可得|PF2|=5|PF1|,|F1F2|=22, |PF1|2+|F1F2|2=|PF2|2,解得|PF2|=533,|PF1|=33, 由椭圆的定义可得2a=533+33=23,所以a=3,c=2,b=1, 所以椭圆的方程为x23+y2=1; 要使△ABF1的内切圆面积最大,只需△ABF1的内切圆的半径r最大. 因为F1(−2, 0),F2(2, 0),设A(x1, y1),B(x2, y2), 显然直线l的斜率不为0,设直线l:x=ty+2,联立x=ty+2x2+3y2=3 , 可得(3+t2)y2+22ty−1=0,则y1+y2=−22t3+t2,y1y2=−13+t2, 则S△ABF1=S△F1F2A+S△F1F2B=12|F1F2|⋅|y1−y2|=2⋅(y1+y2)2−4y1y2 =2⋅(−22t3+t2)2+43+t2=26t2+13+t2, 又S△ABF1=12(|AF1|+|BF1|+|AB|)⋅r=12⋅43⋅r=23r, 故26t2+13+t2=23r,即r=2t2+13+t2=2t2+1+2t2+1≤12, 当且仅当t2+1=2t2+1,即t=±1时等号成立. 所以直线l的方程为y=x−2或y=−x+2. 【答案】 f′(x)=2(a+1)(x+a)2−1x=−x2+2x−a2x(x+a)2,其中a>0, ①当a≥1时,f′(x)≤−x2+2x−1x(x+a)2=−(x−1)2x(x+a)2≤0 恒成立, 所以函数f(x)在区间(0, +∞)内单调递减,无的单调增区间; ②当0查看更多