2004－2005学年度第一学期期末考试

2004－2005学年度第一学期期末考试

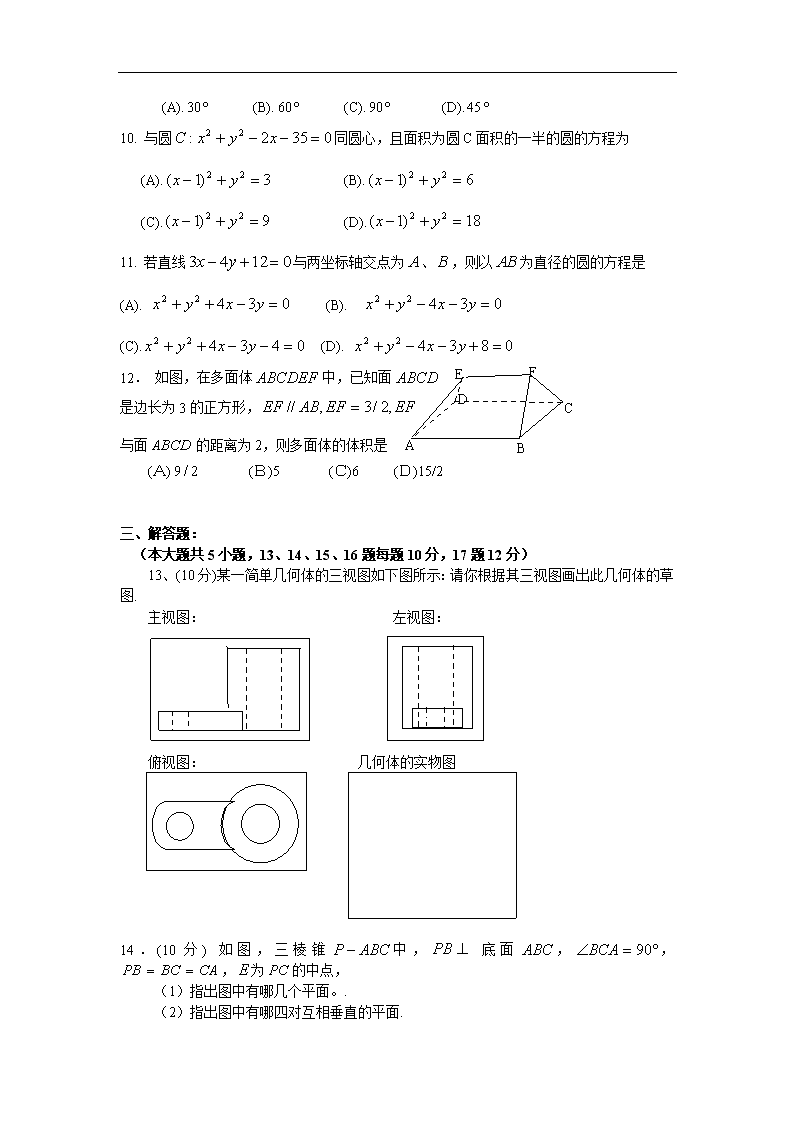
‎2004－2005学年度第一学期期末考试 广州开发区中学高一级数学科学业模块结业试卷 1. 班级_______ 学号_______ 姓名_______ 成绩_______‎ 命题人：安西民 郭云海 吴华东 审题人：熊跃农 一、选择题：下列每小题都给出A,B,C,D四个答案，请将唯一正确的答案的代号填写在下面的表格里（本大题共12小题，每小题4分，共48分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 选项 ‎1. 在空间内，可以确定一个平面的条件是 ‎（A） 两两相交的三条直线 ，且有三个不同的交点 ‎ ‎（B） 三条直线，其中的一条与另外两条直线分别相交 ‎（C） 三个点 （D）两条直线 ‎2. 异面直线是指 ‎（A）空间中两条不相交的直线 ‎（B）平面内的一条直线与平面外的一条直线 ‎ ‎（C）分别位于两个不同平面内的两条直线 ‎ ‎（D）不同在任何一个平面内的两条直线 ‎ ‎3. 点在平面的射影为，且、、两两垂直，那么是的 ‎ (A).内心　　　(B).外心　　　(C).垂心　　　(D).重心 ‎4. 在下列关于直线于平面的命题中真命题是 ‎（A）若且，则（B）若且，则 ‎ ‎（C）若且，则（D）若且，则 ‎ ‎5. 在空间坐标中，点是在坐标平面内的射影，O为坐标原点，则等于 ‎(A). (B). (C). (D). ‎ ‎6. 已知点A(1，2)、B（3，1），线段AB的垂直平分线的方程是 ‎(A). (B). ‎ ‎(C). (D). ‎ ‎7. 已知点(a,2)（a>0）到直线l：x-y+3=0的距离为1，则a等于 ‎(A). (B). (C). (D). 1+‎ ‎8. 直线和直线的位置关系是 ‎ (A).相交但不垂直 (B).垂直 (C). 平行 (D).重合 ‎ ‎9. 直线与直线的夹角为 ‎(A). (B). (C). (D).‎ ‎10. 与圆同圆心，且面积为圆C面积的一半的圆的方程为 ‎(A). (B).‎ ‎(C). (D).‎ ‎11. 若直线与两坐标轴交点为、，则以为直径的圆的方程是 ‎(A). (B). ‎ D E C B A F ‎(C). (D). ‎ ‎12． 如图，在多面体中，已知面 是边长为3的正方形，‎ 与面的距离为2，则多面体的体积是 ‎ (Ａ) (Ｂ)5 (Ｃ)6 (Ｄ)15/2‎ 三、解答题：‎ ‎（本大题共5小题，13、14、15、16题每题10分，17题12分）‎ ‎13、(10分)某一简单几何体的三视图如下图所示：请你根据其三视图画出此几何体的草图.‎ 主视图： 左视图：‎ 俯视图： 几何体的实物图 ‎14．(10分) 如图，三棱锥中， 底面，，，为的中点，‎ ‎ （1）指出图中有哪几个平面。.‎ ‎ （2）指出图中有哪四对互相垂直的平面.‎ A B C E P ‎15、(10分) 已知正三棱锥的侧棱长为2，底面周长为，求这个棱锥的高及体积.‎ A S C B O ‎ ‎ ‎16、(10分)已知定点，动点在直线上运动，当线段最短时，求的坐标.‎ ‎17、（12分）直线经过点，且和圆：相交，截得弦长为，求的方程.‎ ‎2004－2005学年度第一学期期末考试 广州开发区中学高一级数学科学科试卷 班级_______ 学号_______ 姓名_______ 成绩_______‎ 命题人：安西民 郭云海 吴华东 审题人：熊跃农 二、填空题：请将正确答案直接填写在空格里（本大题共4小题，每小题5分，共20分）‎ ‎18．圆和圆的位置关系是的_____.‎ ‎19． 是三直线，是平面，若，且_________（填上一个条件即可），则有.‎ ‎20．以点(1，2)为圆心，与直线相切的圆的方程是________________. ‎ ‎21．球与其内接正方体的体积比是 _____________.‎ ‎22. (15分)如图，平面，四边形是矩形，，分别是的中点.‎ ‎（1）求证：平面.‎ ‎（2）求证：平面平面.‎ E D N C B M A P ‎23. (15分)已知是直线上的动点，是圆的切线，是切点，是圆心.‎ ‎（1）求四边形面积的最小值.‎ ‎（2）当四边形面积最小时，求切线的方程.‎ ‎2004－2005学年度第一学期期末考试 广州开发区中学高一级数学科学业模块结业试题答案 1. 班级_______ 学号_______ 姓名_______ 成绩_______‎ 命题人：安西民 郭云海 吴华东 审题人：熊跃农 一、选择题：下列每小题都给出A,B,C,D四个答案，请将唯一正确的答案的代号填写在下面的表格里（本大题共12小题，每小题4分，共48分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 选项 B D A C C B C B A D A D ‎1. 直线和直线的位置关系是 ‎(A).相交但不垂直 (B).垂直 (C). 平行 (D).重合 ‎2. 异面直线是指 ‎（A）空间中两条不相交的直线 ‎（B）平面内的一条直线与平面外的一条直线 ‎ ‎（C）分别位于两个不同平面内的两条直线 ‎ ‎（D）不同在任何一个平面内的两条直线 ‎ ‎3. 在空间内，可以确定一个平面的条件是 ‎（A） 两两相交的三条直线 ，且有三个不同的交点 ‎ ‎（B） 三条直线，其中的一条与另外两条直线分别相交 ‎（C） 三个点 （D）两条直线 ‎4. 直线的倾斜角为 ‎(A). (B). (C). (D). ‎ ‎5. 在空间坐标中，点是在坐标平面内的射影，O为坐标原点，则的长等于 ‎(A). (B). (C). (D). ‎ ‎6. 已知点A(1，2)、B（3，1），线段AB的垂直平分线的方程是 ‎(A). (B). ‎ ‎(C). (D). ‎ ‎7. 已知点(a,2)（a>0）到直线l：x-y+3=0的距离为1，则a等于 ‎(A). (B). (C). (D). 1+‎ ‎8. 点在平面上的射影为，且==，那么是的 ‎(A). 垂心　 (B).外心　　　 (C). 内心　　 　(D).重心 ‎9. 在下列关于直线与平面的命题中真命题是 ‎（A）若且，则（B）若且，则 ‎（C）若且，则（D）若且，则 ‎ ‎10. 与圆同圆心，且面积为圆C面积的一半的圆的方程为 ‎(A). (B).‎ ‎(C). (D).‎ ‎11. 若直线与两坐标轴交点为、，则以为直径的圆的方程是 ‎(A). (B). ‎ ‎(C). (D). ‎ ‎12． 如图，在多面体中，‎ 已知面是边长为3的正方形，‎ 与面 的距离为2，则多面体的体积是 ‎ (Ａ). (Ｂ). 5 ‎ ‎(Ｃ). 6 (Ｄ). 15/2‎ 二、解答题：（写出必要的解题过程）‎ ‎（本大题共5小题，13、14、15、16题每题10分，17题12分）‎ ‎13、(10分)某一简单几何体的实物图如下图所示：请你根据其实物图画出此几何体的三视图.‎ 几何体的实物图 主视图： ‎ ‎ ‎ 左视图： 俯视图：‎ ‎14．(10分) 如图，三棱锥中， 底面，，，为的中点，‎ ‎ （1）指出图中有哪几个平面。.‎ ‎ （2）指出图中有哪四对互相垂直的平面.‎ A B C E P ‎ （1）图中有平面ABC，平面PAB，平面PBC，平面PCA，平面ABE ‎（2）图中有四对互相垂直的平面 ‎ 平面PAB平面ABC ‎ 平面PBC平面ABC ‎ 平面PBC平面PCA ‎ 平面ABE平面PCA ‎15、(10分) 已知正三棱锥的侧棱长为2，底面周长为，求这个棱锥的高及体积.‎ ‎ ‎ A S C B O 解：如图：为正三棱锥 在平面上的射影为 的中心。‎ ‎16、(10分)已知定点，动点在直线上运动，当线段最短时，求的坐标.‎ Y X 解：如图。易知当的连线与已知直线垂直 时，的长度最短。‎ 直线的斜率 的斜率 的斜率的方程为：‎ 的坐标为 ‎17、（12分）直线经过点，且和圆：相交，截得弦长为，求的方程.‎ Y 解：如图易知直线的斜率存在，‎ 设直线的方程为 圆：的圆心为（0，0）‎ X 半径，圆心到直线的距离 在中，，‎ ‎，或 的方程为或 ‎2004－2005学年度第一学期期末考试 广州开发区中学高一级数学科学科试卷 班级_______ 学号_______ 姓名_______ 成绩_______‎ 命题人：安西民 郭云海 吴华东 审题人：熊跃农 一、填空题：请将正确答案直接填写在空格里（本大题共4小题，每小题5分，共20分）‎ ‎18．圆和圆的位置关系是的相交.‎ ‎19． 是三直线，是平面，若，且（填上一个条件即可），则有.‎ ‎20．以点(1，2)为圆心，与直线相切的圆的方程是. ‎ ‎21．球与其内接正方体的体积比是 .‎ 二、解答题：（写出必要的解题过程）‎ ‎（本大题共2小题，每题15分，17题12分）‎ ‎22. (15分)如图，平面，四边形是矩形，，分别是的中点.‎ ‎（1）求证：平面.‎ ‎（2）求证：平面平面.‎ E D N C B M A P 提示：‎ ‎（1）证：为平行四边形 ‎（2）证：‎ ‎，‎ 平面平面 ‎23. (15分)已知是直线上的动点，是圆的切线，是切点，是圆心.‎ ‎（1）求四边形面积的最小值.‎ ‎（2）当四边形面积最小时，求切线的方程.‎ 略解：‎ 的方程略。‎