新教材数学人教B版必修第二册课件：6-3-1　平面向量基本定理

新教材数学人教B版必修第二册课件：6-3-1　平面向量基本定理

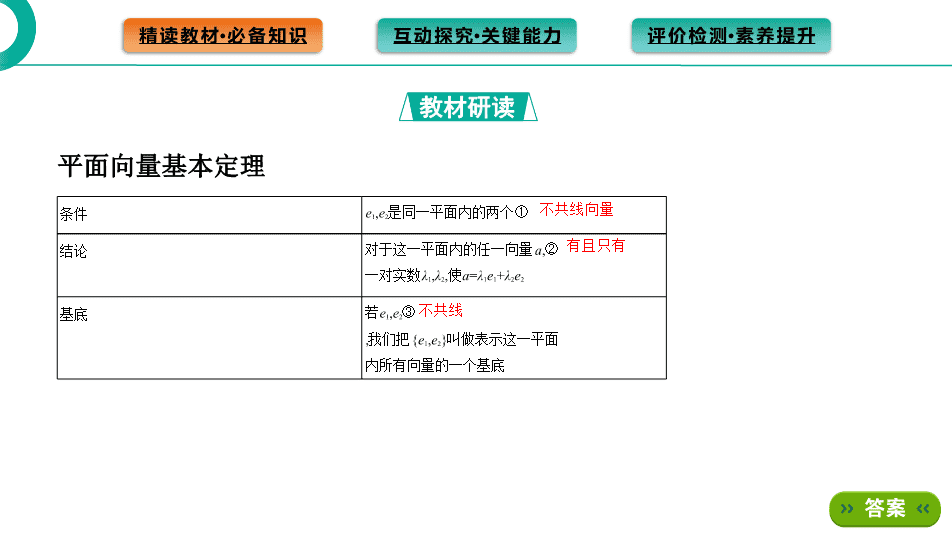
精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 第六章　平面向量及其应用 §6.3　平面向量基本定理及坐标表示 6.3.1　平面向量基本定理 第 一 篇 教 材 过 关 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 　　问题1:在物理中,我们学习了力的分解,即一个力可以分解为两个不同方 向的力,试想平面内的任一向量是否可以分解为其他两个向量的和. 情景导学 精读教材·必备知识 答案　可以. 问题2:如果e1,e2是两个不共线的向量,那么与e1,e2在同一平面内的任一 向量a能否用e1,e2表示?依据是什么? 答案　能.依据数乘向量和平行四边形法则. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 平面向量基本定理 教材研读 条件 e1,e2是同一平面内的两个① 结论 对于这一平面内的任一向量a,② 一 对实数λ1,λ2,使a=λ1e1+λ2e2 基底 若e1,e2③ ,我们把{e1,e2}叫做表示这一平 面 内所有向量的一个基底 不共线向量 有且只有 不共线 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 思考1:0能与另外一个向量a构成基底吗? 提示　不能,基底是不共线的,0与任意向量都是共线的. 思考2:同一平面内向量的基底是唯一的吗? 提示　不唯一,但基底一旦确定,平面内任一向量都可以用这一基底唯一表示. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究一　基底的概念 互动探究·关键能力 例1 (多选题)设O是平行四边形ABCD两对角线的交点,则下列向量组中,可作 为这个平行四边形所在平面内一个基底的是  (　　) A.{  ,  }　 B.{  ,  } C.{  ,  }　 D.{  ,  } AD  AB  DA  BC  CA  DC  OD  OB  AC 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　 A中,  与  不共线;B中,  =-  ,则  与  共线;C中,  与  不共 线;D中,  =-  ,则  与  共线.由平面向量基底的概念知,只有不共线的两 个向量才能构成一个基底.故选AC. AD  AB  DA  BC  DA  BC  CA  DC  OD  OB  OD  OB  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 思维突破 能作为向量基底的条件 (1)两个向量不共线,基底的选择是不唯一的. (2)零向量与任意向量共线,不能作为基底. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 1-1　设{e1,e2}是平面内一个基底,则下面四组向量中,不能作为基底的是  ( 　) A.{e1+e2,e1-e2}　 B.{3e1-2e2,4e2-6e1} C.{e1+2e2,e2+2e1}　 D.{e2,e2+e1} 解析　∵4e2-6e1=-2(3e1-2e2),∴两个向量共线,不能作为基底. B 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 1-2　已知e1、e2不共线,a=e1+2e2,b=2e1+λe2,要使a,b能作为平面内的一组基底, 则实数λ的取值范围为　　 　 .(-∞,4)∪(4,+∞) 解析　若a,b能作为平面内的一组基底,则a与b不共线,则a≠kb(k∈R),又a=e1+2 e2,b=2e1+λe2, ∴λ≠4. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究二　用基底表示向量 例2 (2020江苏南京高一期中)如图所示,在△OAB中,  =a,  =b,点M是AB上 靠近点B的一个三等分点,点N是OA上靠近点A的一个四等分点.若OM与BN相 交于点P,求  .   OA  OB  OP  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　∵  =a,  =b, ∴  =  +  =  +    =  + (  -  )= a+ b. ∵  与  共线,可设  =t  = a+ b. OA  OB  OM  OA  AM  OA  2 3 AB  OA  2 3 OB  OA  1 3 2 3 OP  OM  OP  OM  3 t 2 3 t 又  与  共线,可设  =s  ,则  =  +s  =   +s(  -  )= (1-s)a+sb, ∴  解得  ∴  = a+ b. NP  NB  NP  NB  OP  ON  NB  3 4 OA  OB  ON  3 4 3 (1- ) ,4 3 2 ,3 ts s t     9 ,10 3,5 t s     OP  3 10 3 5 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 思维突破 用基底表示向量的方法 (1)选基底:选取两个不共线的向量作为基底表示其他向量. (2)依据:①向量加法的三角形法则和平行四边形法则;②向量减法的几何意义; ③数乘向量的几何意义. (3)方法: ①运用向量的线性运算法则对所求向量进行转化; ②通过列方程(组)求解. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 2-1 (多选题)(2020山东青岛高一期末)D,E,F分别为△ABC的边BC,CA,AB上 的中点,且  =a,  =b,则下列结论正确的有  (　　) A.  =- a-b　　B.  =a+ b C.  =- a+ b　　D.  = a BC  CA  AD  1 2 BE  1 2 CF  1 2 1 2 EF  1 2 ABC 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　如图所示,     =  +  =-b+   =- a-b,A正确;  =  +  =a+ b,B正确;  =  +  =-b- a,  =  +   =b+ (-b-a)= b- a,C正确;  =   =- a,D不正确. AD  AC  CD  1 2 CB  1 2 BE  BC  CE  1 2 AB  AC  CB  CF  CA  1 2 AB  1 2 1 2 1 2 EF  1 2 CB  1 2 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 2-2　如图所示,已知在▱ ABCD中,E,F分别是BC,DC边上的中点.若  =a,  =b,试用a,b表示向量  ,  .   AB  AD  DE  BF  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　∵四边形ABCD是平行四边形,E,F分别是BC,DC边上的中点, ∴  =  =2  ,  =  =2  , ∴  =   = b,  =   =   =-   =- a, ∴  =  +  +  =-  +  +  =-b+a+ b=a- b,   =  +  =  +  =b- a. AD  BC  BE  CD  BA  CF  BE  1 2 AD  1 2 CF  1 2 CD  1 2 BA  1 2 AB  1 2 DE  DA  AB  BE  AD  AB  BE  1 2 1 2 BF  BC  CF  AD  CF  1 2 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究三　利用平面向量基本定理解决平面几何问题 例3 (易错题)如图所示,L,M,N分别为△ABC的边BC,CA,AB上的点,且  =l,   =m,  =n,若  +  +  =0,求证:l=m=n.   BL BC CM CA AN AB AL  BM  CN  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 证明　令  =a,  =b,{a,b}为一个基底,根据已知有  =la,  =mb. ∵  =  +  =-a-b, BC  CA  BL  CM  AB  AC  CB  则有  =n  =-na-nb, ∴  =  +  =(l-1)a-b,   =  +  =a+mb , AN  AB  AL  AB  BL  BM  BC  CM  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升   =  +  =-na+(1-n)b, 又  +  +  =0, ∴(l-n)a+(m-n)b=0. 根据平面向量基本定理, 有l-n=m-n=0, 即l=m=n. CN  CA  AN  AL  BM  CN  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 易错点拨 常因不能恰当选择基底而找不到突破口,导致无从下手,造成失分. 平面向量基本定理在解决几何问题中的作用 (1)平面向量基本定理提供了向量的几何表示方法. (2)由平面向量基本定理可知,任意向量都可以用一个与它共线的非零向量线 性表示,而且这种表示是唯一的.因此,恰当选择基底是解决问题的关键. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 3-1　用向量法证明三角形的三条中线交于一点. 证明　如图,设D,E,F分别是△ABC的三边BC,AC,AB的中点,   令  =a,  =b, 则  =a-b,  =a- b,  =- a+b. AC  BC  AB  AD  1 2 BE  1 2 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 设AD与BE交于点G, 且  =λ  ,  =μ  , 则有  =λa- b,  =- a+μb, 又有  =  +  =  a+(μ-1)b, ∴  解得λ=μ= , ∴  = a- b,  =  +  =-a+ a- b=- a- b= × (-a-b). AG  AD  BG  BE  AG  2 λ BG  2 μ AG  AB  BG  1- 2 μ     1- ,2 - -1,2 μλ λ μ     2 3 AG  2 3 1 3 CG  CA  AG  2 3 1 3 1 3 1 3 2 3 1 2 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 而  = (-a-b),∴  =   . ∴点G是CF上一点, ∴三角形的三条中线交于一点. CF  1 2 CG  2 3 CF  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 1.{e1,e2}是平面内一个基底,下面说法正确的是  (　　) A.若实数λ1,λ2使λ1e1+λ2e2=0,则λ1=λ2=0 B.空间内任一向量a可以表示为a=λ1e1+λ2e2(λ1,λ2为实数) C.对实数λ1,λ2,λ1e1+λ2e2不一定在该平面内 D.对平面内任一向量a,使a=λ1e1+λ2e2的实数λ1,λ2有无数对 课堂检测 评价检测·素养提升 A 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　由基底的定义可以知道,e1和e2是平面上不共线的两个向量,所以若 实数λ1,λ2使λ1e1+λ2e2=0,则λ1=λ2=0,不是空间任一向量都可以表示为a=λ1e1+λ2e2, 而是平面中的任一向量a,可以表示为a=λ1e1+λ2e2的形式,此时实数λ1,λ2有且只 有一对,而对实数λ1,λ2,λ1e1+λ2e2一定在平面内,所以A正确. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 2.设D为△ABC所在平面内一点,若  =3  ,则  (　　) A.  =-   +   　 B.  =   -   C.  =   +   　 D.  =   -   BC  CD  AD  1 3 AB  4 3 AC  AD  1 3 AB  4 3 AC  AD  4 3 AB  1 3 AC  AD  4 3 AB  1 3 AC  A 解析　因为  =3  ,所以  -  =3(  -  )=3  -3  , 所以3  =4  -  ,所以  =   -   =-   +   . BC  CD  AC  AB  AD  AC  AD  AC  AD  AC  AB  AD  4 3 AC  1 3 AB  1 3 AB  4 3 AC  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 3.已知向量a,b不共线,且  =a+2b,  =-5a+6b,  =7a-2b,则一定共线的三点是   (　　) A.A,B,D　 B.A,B,C C.B,C,D　 D.A,C,D AB  BC  CD  解析　∵  =-5a+6b,  =7a-2b,∴  =  +  =2a+4b,又  =a+2b,∴2  =  ,∴  ∥  . 又∵  与  有公共点B,∴A,B,D三点共线. BC  CD  BD  BC  CD  AB  AB  BD  AB  BD  AB  BD  A 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 4.已知向量a,b是一组基底,实数x,y满足(3x-4y)a+(2x-3y)b=6a+3b,则x-y的值为 　　　 .3 解析　因为a,b是一组基底,所以a与b不共线. 因为(3x-4y)a+(2x-3y)b=6a+3b, 所以  解得  所以x-y=3. 3 -4 6, 2 -3 3, x y x y    6, 3, x y    精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 5.如图,平面内有三个向量  、  、  ,其中  与  的夹角为120°,  与  的夹角为30°,且|  |=|  |=1,|  |=2  .若  =λ  +μ  (λ,μ∈R),求λ+μ的值.   OA  OB  OC  OA  OB  OA  OC  OA  OB  OC  3 OC  OA  OB  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　如图,以OC为对角线作▱ OMCN,使得M在直线OA上,N在直线OB上,   则存在λ,μ,使  =λ  ,  =μ  , 即  =  +  =λ  +μ  . ∵∠MON=120°,∠MOC=30°, ∴∠OCM=90°, ∴在Rt△COM中,|  |=2  , OM  OA  ON  OB  OC  OM  ON  OA  OB  OC  3 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 ∴|  |=4,|  |=2,∴  =4  , 又|  |=|  |=2,∴  =2  , ∴  =4  +2  ,即λ=4,μ=2, ∴λ+μ=6. OM  MC  OM  OA  ON  MC  ON  OB  OC  OA  OB  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 数学运算——利用方程思想求向量等式中的参数 在△ABC中,点P是AB上一点,且  =   +   ,Q是BC的中点,AQ与CP的交点 为M,又  =t  ,求t的值. 审:条件中  用基底{  ,  }表示,而  =t  ,要求t的值,需  也用基底{  ,   }表示,利用方程思想求解. 联:三点共线的向量问题,把向量用基底表示,建立方程组. CP  2 3 CA  1 3CB  CM  CP  CP  CA  CB  CM  CP  CM  CA  CB  素养演练 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解:∵  =   +   ,∴3  =2  +  , 即2  -2  =  -  ,∴①　　　 , 即P为AB的一个三等分点,如图所示.   CP  2 3 CA  1 3CB  CP  CA  CB  CP  CA  CB  CP  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 设  =x  +(1-x)  =②　　　　　　　　 , 而  =  -  ,∴  =③　　　　　　 . 又  =  -  =-  +   ,由已知  =t  , 可得   +    =t  , 又  ,  不共线,∴④　　　 ,解得t= . CM  CQ  CA  CB  AB  AC  CM  CP  CA  PA  AC  1 3 AB  CM  CP  2 x AB  -12 x     AC  1- 3AC AB      AB  AC  3 4 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 思:平面内任一向量利用平面向量基本定理都可以表示为同一平面内两个不 共线向量e1,e2的线性组合λ1e1+λ2e2. 具体求λ1,λ2时的两种方法: (1)直接利用三角形法则、平行四边形法则及向量共线定理. (2)利用待定系数法,即利用定理中λ1,λ2的唯一性列方程组求解. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 变式训练 (变结论)本例中,试问点M在AQ的什么位置? 解析　由例题知  =    +  ·  及x= ,  =2  知,  = x(  -  )+    =    +(1-x)  =x  +(1-x)  =  .因此,点M是AQ的中点. CM  2 x AB  -2 2 x AC  1 2 CB  CQ  CM  1 2 CB  CA  2- 2 x CA  2 x CB  CA  CQ  CA  2 CQ CA  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 针对训练 　在△ABC中,M是AB边所在直线上任意一点,若  =-2  +λ  ,则λ=  (　　) A.1　 B.2　 C.3　 D.4 CM  CA  CB  C 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　∵ M是△ABC中 AB边所在直线上任意一点, ∴存在实数μ,使得  =μ  , 即  -  =μ(  -  ), 化简,得  =    +    , ∵  =-2  +λ  , ∴  解得λ=3,μ=- . AM  MB  CM  CA  CB  CM  CM  1 1 μ CA  1 μ μ CB  CM  CA  CB  1 -2,1 ,1 μ μ λμ       3 2