2019高三数学理北师大版一轮课时分层训练26　平面向量的概念及线性运算

2019高三数学理北师大版一轮课时分层训练26　平面向量的概念及线性运算

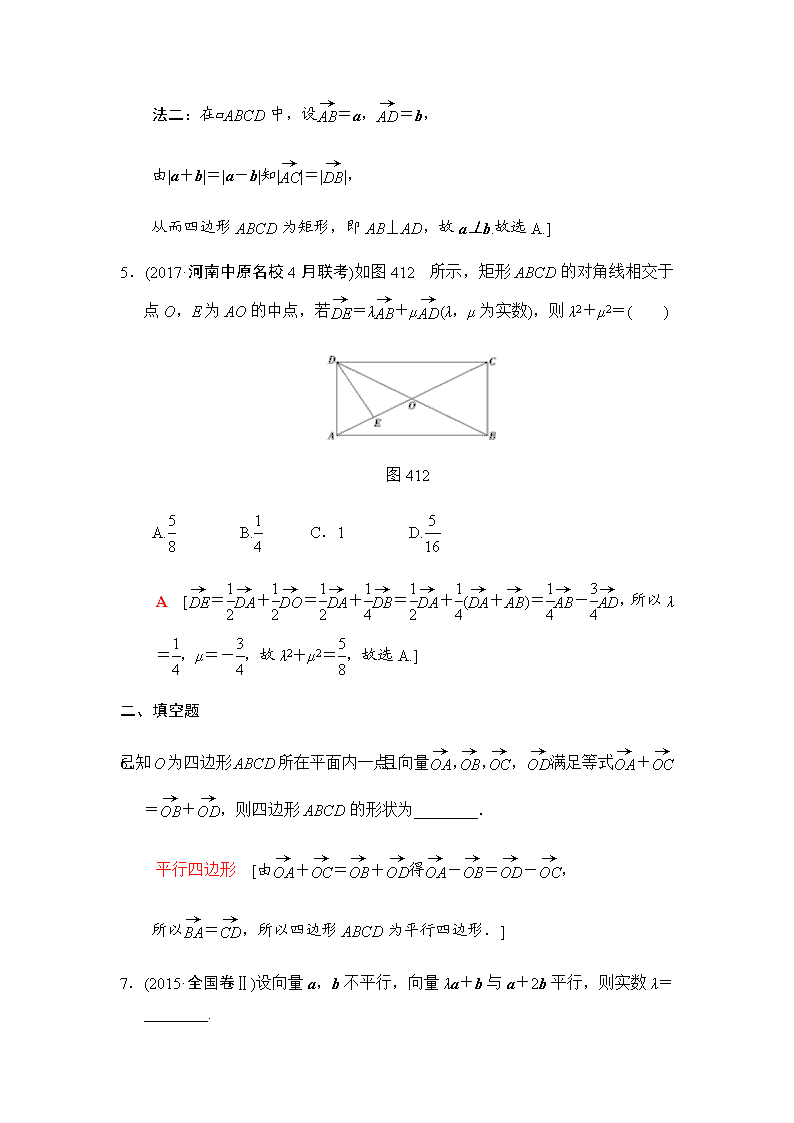
课时分层训练(二十六)　平面向量的概念及线性运算 ‎(对应学生用书第250页)‎ A组　基础达标 一、选择题 ‎1．给出下列命题：①零向量的长度为零，方向是任意的；②若a，b都是单位向量，则a＝b；③向量与相等．则所有正确命题的序号是(　　)‎ A．①　　　 B．③‎ C．①③ D．①②‎ A　[根据零向量的定义可知①正确；根据单位向量的定义可知，单位向量的模相等，但方向不一定相同，故两个单位向量不一定相等，故②错误；向量与互为相反向量，故③错误．]‎ ‎2．(2018·武汉调研)设a是非零向量，λ是非零实数，则下列结论正确的是(　　) ‎ ‎【导学号：79140147】‎ A．a与－λa的方向相反 B．|－λa|≥|a|‎ C．a与λ2a的方向相同 D．|－λa|≥|λ|a C　[A中，当λ＜0时，a与－λa方向相同，故A不正确；B中，当－1＜λ＜1时，|－λa|＜|a|，故B不正确；C中，因为λ2＞0，所以a与λ2a方向相同，故C正确；D中，向量不能比较大小，故D不正确，故选C.]‎ ‎3．(2017·广东东莞二模)如图411所示，已知＝3，＝a，＝b，＝c，则下列等式中成立的是(　　)‎ 图411‎ A．c＝b－a B．c＝2b－a C．c＝2a－b D．c＝a－b A　[因为＝3，＝a，＝b，所以＝＋＝＋＝＋(－)＝－＝b－a，故选A.]‎ ‎4．(2017·全国卷Ⅱ)设非零向量a，b满足|a＋b|＝|a－b|，则(　　)‎ A．a⊥b B．|a|＝|b|‎ C．a∥b D．|a|＞|b|‎ A　[法一：∵|a＋b|＝|a－b|，∴|a＋b|2＝|a－b|2.‎ ‎∴a2＋b2＋2a·b＝a2＋b2－2a·b.‎ ‎∴a·b＝0.∴a⊥b.‎ 故选A.‎ 法二：在▱ABCD中，设＝a，＝b，‎ 由|a＋b|＝|a－b|知||＝||，‎ 从而四边形ABCD为矩形，即AB⊥AD，故a⊥b.故选A.]‎ ‎5．(2017·河南中原名校4月联考)如图412所示，矩形ABCD的对角线相交于点O，E为AO的中点，若＝λ＋μ(λ，μ为实数)，则λ2＋μ2＝(　　)‎ 图412‎ A.　　　　B. C．1　　　　D. A　[＝＋＝＋＝＋(＋)＝－，所以λ＝，μ＝－，故λ2＋μ2＝，故选A.]‎ 二、填空题 ‎6．已知O为四边形ABCD所在平面内一点，且向量，，，满足等式＋＝＋，则四边形ABCD的形状为________．‎ 平行四边形　[由＋＝＋得－＝－，‎ 所以＝，所以四边形ABCD为平行四边形．]‎ ‎7．(2015·全国卷Ⅱ)设向量a，b不平行，向量λa＋b与a＋2b平行，则实数λ＝________.‎ 　[∵λa＋b与a＋2b平行，∴λa＋b＝t(a＋2b)，‎ 即λa＋b＝ta＋2tb，∴解得]‎ ‎8．在△ABC中，点M，N满足＝2，＝.若＝x＋y，则x＝________；y＝________. ‎ ‎【导学号：79140148】‎ 　－　[∵＝2，∴＝.‎ ‎∵＝，∴＝(＋)，‎ ‎∴＝－＝(＋)－ ‎＝－.‎ 又＝x＋y，∴x＝，y＝－.]‎ 三、解答题 ‎9．如图413，在△ABC中，D，E分别为BC，AC边上的中点，G为BE上一点，且GB＝2GE，设＝a，＝b，试用a，b表示，.‎ 图413‎ ‎[解]　＝(＋)＝a＋b.‎ ＝＋＝＋＝＋(＋)‎ ‎＝＋(－)‎ ‎＝＋ ‎＝a＋b.‎ ‎10．设e1，e2是两个不共线的向量，已知＝2e1－8e2，＝e1＋3e2，＝2e1－e2.‎ ‎(1)求证：A，B，D三点共线；‎ ‎(2)若＝3e1－ke2，且B，D，F三点共线，求k的值．‎ ‎[解]　(1)证明：由已知得＝－＝(2e1－e2)－(e1＋3e2)＝e1－4e2，‎ ‎∵＝2e1－8e2，∴＝2.‎ 又∵与有公共点B，‎ ‎∴A，B，D三点共线．‎ ‎(2)由(1)可知＝e1－4e2，‎ ‎∵＝3e1－ke2，且B，D，F三点共线，‎ ‎∴＝λ(λ∈R)，‎ 即3e1－ke2＝λe1－4λe2，‎ 即解得k＝12.‎ B组　能力提升 ‎11．(2017·河北衡水中学三调考试)在△ABC中，＝，若P是直线BN上的一点，且满足＝m＋，则实数m的值为(　　) ‎ ‎【导学号：79140149】‎ A．－4 B．－1‎ C．1 D．4‎ B　[根据题意设＝n(n∈R)，则＝＋＝＋n＝＋n(－)＝＋n＝(1－n)＋，又＝m＋，∴解得故选B.]‎ ‎12．设O在△ABC的内部，D为AB的中点，且＋＋2＝0，则△ABC的面积与△AOC的面积的比值为(　　)‎ A．3　　 B．4 C．5　　　　D．6‎ B　[如图，∵D为AB的中点，则＝(＋)，又＋＋2＝0，‎ ‎∴＝－，∴O为CD的中点，‎ 又∵D为AB中点，∴S△AOC＝S△ADC＝S△ABC，则＝4.]‎ ‎13．(2017·辽宁大连高三双基测试)如图414，在△ABC中，AB＝2，BC＝3，∠ABC＝60°，AH⊥BC于点H，M为AH的中点．若＝λ＋μ，则λ＋μ＝________.‎ 图414‎ 　[因为AB＝2，∠ABC＝60°，AH⊥BC，所以BH＝1.因为BC＝3，所以BH＝BC.‎ 因为点M为AH的中点，所以＝＝(＋)＝＝＋，又＝λ＋μ，所以λ＝，μ＝，所以λ＋μ＝.]‎ ‎14．已知O，A，B是不共线的三点，且＝m＋n(m，n∈R). ‎ ‎【导学号：79140150】‎ ‎(1)若m＋n＝1，求证：A，P，B三点共线；‎ ‎(2)若A，P，B三点共线，求证：m＋n＝1.‎ ‎[证明]　(1)若m＋n＝1，‎ 则＝m＋(1－m) ‎＝＋m(－)，‎ ‎∴－＝m(－)，‎ 即＝m，∴与共线．‎ 又∵与有公共点B，‎ ‎∴A，P，B三点共线．‎ ‎(2)若A，P，B三点共线，‎ 则存在实数λ，使＝λ，‎ ‎∴－＝λ(－)．‎ 又＝m＋n.‎ 故有m＋(n－1)＝λ－λ，‎ 即(m－λ)＋(n＋λ－1)＝0.‎ ‎∵O，A，B不共线，∴，不共线，‎ ‎∴∴m＋n＝1.‎