- 2021-06-30 发布 |
- 37.5 KB |
- 19页

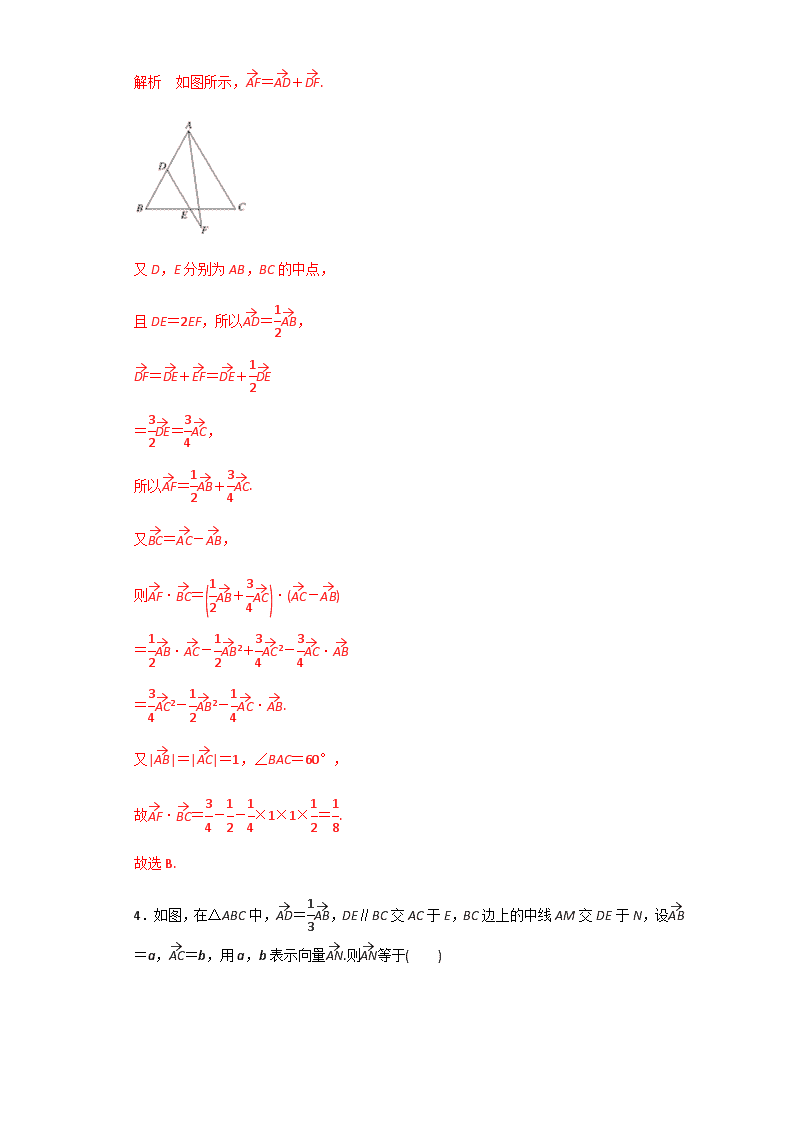
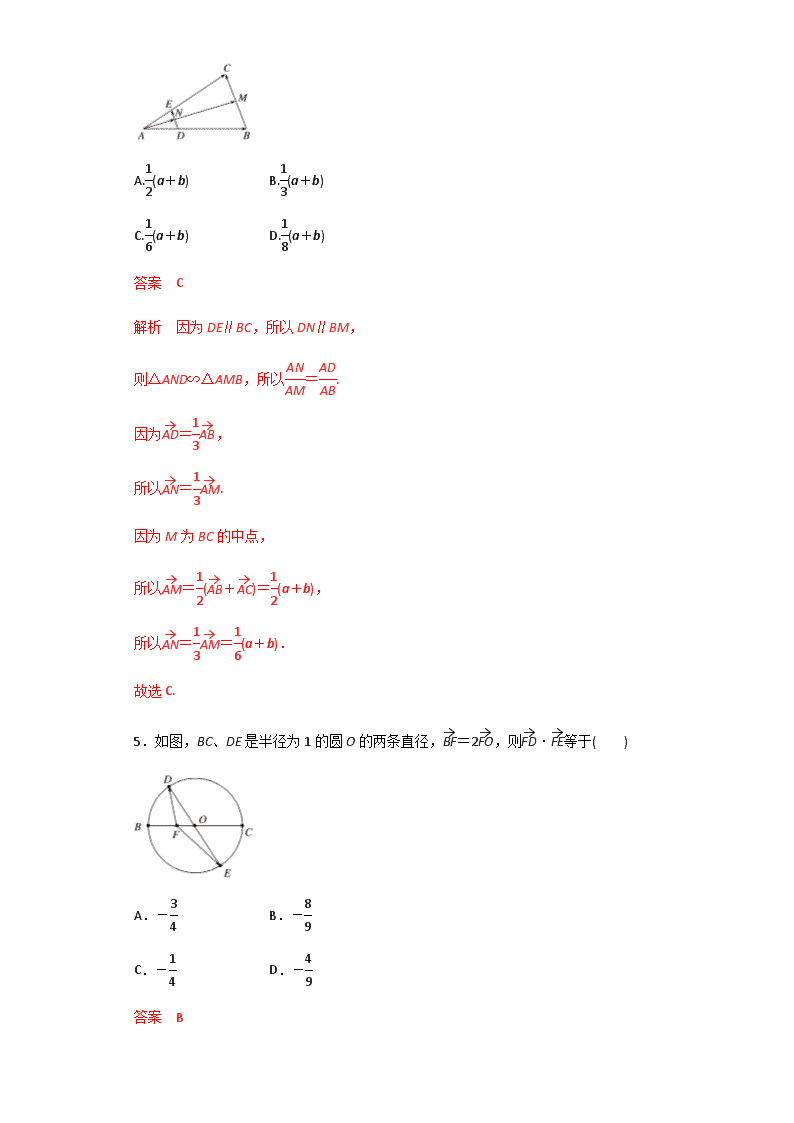
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
专题08 平面向量-2017年高考数学(理)备考学易黄金易错点
专题08 平面向量 2017年高考数学(理)备考学易黄金易错点 1.已知向量=,=,则∠ABC等于( ) A.30°B.45°C.60°D.120° 答案 A 解析 ∵||=1,||=1, cos∠ABC==,∴∠ABC=30°. 2.已知非零向量m,n满足4|m|=3|n|,cos〈m,n〉=.若n⊥(tm+n),则实数t的值为( ) A.4B.-4C.D.- 答案 B 3.已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则·的值为( ) A.- B. C. D. 答案 B 解析 如图所示,=+. 又D,E分别为AB,BC的中点, 且DE=2EF,所以=, =+=+ ==, 所以=+. 又=-, 则·=·(-) =·-2+2-· =2-2-·. 又||=||=1,∠BAC=60°, 故·=--×1×1×=. 故选B. 4.如图,在△ABC中,=,DE∥BC交AC于E,BC边上的中线AM交DE于N,设=a,=b,用a,b表示向量.则等于( ) A.(a+b) B.(a+b) C.(a+b) D.(a+b) 答案 C 解析 因为DE∥BC,所以DN∥BM, 则△AND∽△AMB,所以=. 因为=, 所以=. 因为M为BC的中点, 所以=(+)=(a+b), 所以==(a+b). 故选C. 5.如图,BC、DE是半径为1的圆O的两条直径,=2,则·等于( ) A.- B.- C.- D.- 答案 B 解析 ∵=2,圆O的半径为1,∴||=, ∴·=(+)·(+)=2+·(+)+·=()2+0-1=-. 6.在△ABC中,=(cos32°,cos58°),=(sin60°sin118°,sin120°sin208°),则△ABC的面积为( ) A. B. C. D. 答案 B 解析 ||===1, =, 所以||==. 则·=cos32°×cos28°-sin32°×sin28° =(cos32°cos28°-sin32°sin28°) =cos(32°+28°)=cos60°=, 故cos〈,〉===. 又〈,〉∈0°,180°],所以〈,〉=60°, 故B=180°-〈,〉=180°-60°=120°. 故△ABC的面积为 S=×||×||sinB =×1××sin120°=.故选B. 7.如图,在半径为1的扇形AOB中,∠AOB=60°,C为弧上的动点,AB与OC交于点P,则·的最小值是_____________________________________________________. 答案 - 8.已知向量a,b,|a|=1,|b|=2.若对任意单位向量e,均有|a·e|+|b·e|≤,则a·b的最大值是________. 答案 解析 由已知可得: ≥|a·e|+|b·e|≥|a·e+b·e|=|(a+b)·e|, 由于上式对任意单位向量e都成立. ∴≥|a+b|成立. ∴6≥(a+b)2=a2+b2+2a·b=12+22+2a·b. 即6≥5+2a·b,∴a·b≤. 易错起源1、平面向量的线性运算 例1、(1)设0<θ<,向量a=(sin2θ,cosθ),b=(cosθ,1),若a∥b,则tanθ=______. (2)(2016·课标全国乙)设D为△ABC所在平面内一点,=3,则( ) A.=-+ B.=- C.=+ D.=- 答案 (1) (2)A 【变式探究】(1)在△ABC中,AB=2,BC=3,∠ABC=60°,AD为BC边上的高,O为AD的中点,若=λ+μ,则λ+μ等于( ) A.1 B. C. D. (2)如图,正方形ABCD中,点E是DC的中点,点F是BC的一个三等分点,那么等于( ) A.- B.+ C.+ D.- 答案 (1)D (2)D 解析 (1)∵=+=+, ∴2=+, 即=+. 故λ+μ=+=. (2)在△CEF中,有=+. 因为点E为DC的中点,所以=. 因为点F为BC的一个三等分点,所以=. 所以=+=+ =-,故选D. 【名师点睛】 (1)对于平面向量的线性运算,要先选择一组基底;同时注意共线向量定理的灵活运用.(2)运算过程中重视数形结合,结合图形分析向量间的关系. 【锦囊妙计,战胜自我】 1.在平面向量的化简或运算中,要根据平面向量基本定理选好基底,变形要有方向不能盲目转化. 2.在用三角形加法法则时,要保证“首尾相接”,结果向量是第一个向量的起点指向最后一个向量终点所得的向量;在用三角形减法法则时,要保证“同起点”,结果向量的方向是指向被减向量. 易错起源2、平面向量的数量积 例2、(1)如图,在平行四边形ABCD中,已知AB=8,AD=5,=3,·=2,则·的值是________. (2)若b=,|a|=2|b|,且(a+b)·b=-2,则向量a,b的夹角为( ) A. B. C. D. 答案 (1)22 (2)C (2)b2=cos2+cos2 =cos2+sin2=1, 所以|b|=1,|a|=2. 由(a+b)·b=-2,可得a·b+b2=-2, 故a·b=-. 故cos〈a,b〉===-. 又〈a,b〉∈0,π],所以〈a,b〉=,故选C. 【变式探究】(1)已知点A,B,C,D在边长为1的方格点图的位置如图所示,则向量在 方向上的投影为( ) A.- B.-1 C.- D. (2)已知正方形ABCD的边长为1,点E是AB边上的动点,则·的值为________;·的最大值为________. 答案 (1)A (2)1 1 解析 (1)不妨以点A为坐标原点,建立如图所示的平面直角坐标系,易得=(-2,3),=(4,2),所以向量在方向上的投影为==-. 故选A. (2)方法一 分别以射线AB,AD为x轴,y轴的正方向建立平面直角坐标系, 则A(0,0),B(1,0),C(1,1),D(0,1),设E(t,0),t∈0,1],则=(t,-1),=(0,-1),所以 eq o(DE,sup6(→))·=(t,-1)·(0,-1)=1. 因为=(1,0),所以·=(t,-1)·(1,0)=t≤1, 故·的最大值为1. 方法二 由图知, 无论E点在哪个位置,在方向上的投影都是CB=1,∴·=||·1=1, 当E运动到B点时,在方向上的投影最大即为DC=1, ∴(·)max=||·1=1. 【名师点睛】 (1)数量积的计算通常有三种方法:数量积的定义,坐标运算,数量积的几何意义; (2)可以利用数量积求向量的模和夹角,向量要分解成题中模和夹角已知的向量进行计算. 【锦囊妙计,战胜自我】 1.数量积的定义:a·b=|a||b|cosθ. 2.三个结论 (1)若a=(x,y),则|a|==. (2)若A(x1,y1),B(x2,y2),则 ||=. (3)若a=(x1,y1),b=(x2,y2),θ为a与b的夹角, 则cosθ==. 易错起源3、平面向量与三角函数 例3、已知函数f(x)=2cos2x+2sinxcosx(x∈R). (1)当x∈0,)时,求函数f(x)的单调递增区间; (2)设△ABC的内角A,B,C的对边分别为a,b,c,且c=3,f(C)=2,若向量m=(1,sinA)与向量n=(2,sinB)共线,求a,b的值. 解 (1)f(x)=2cos2x+sin2x=cos2x+sin2x+1=2sin(2x+)+1, 令-+2kπ≤2x+≤+2kπ,k∈Z, 解得kπ-≤x≤kπ+,k∈Z, 因为x∈0,), 所以f(x)的单调递增区间为0,]. (2)由f(C)=2sin(2C+)+1=2, 得sin(2C+)=, 而C∈(0,π),所以2C+∈(,), 所以2C+=π,解得C=. 因为向量m=(1,sinA)与向量n=(2,sinB)共线, 所以=. 由正弦定理得=,① 由余弦定理得c2=a2+b2-2abcos, 即a2+b2-ab=9.② 联立①②,解得a=,b=2. 【变式探究】已知平面向量a=(sinx,cosx),b=(sinx,-cosx),c=(-cosx,-sinx),x∈R,函数f(x)=a·(b-c). (1)求函数f(x)的单调递减区间; (2)若f=,求sinα的值. 解 (1)因为a=(sinx,cosx),b=(sinx,-cosx), c=(-cosx,-sinx), 所以b-c=(sinx+cosx,sinx-cosx), f(x)=a·(b-c)=sinx(sinx+cosx)+cosx(sinx-cosx). 则f(x)=sin2x+2sinxcosx-cos2x =sin2x-cos2x=sin. 则当2kπ+≤2x-≤2kπ+,k∈Z, 即kπ+≤x≤kπ+,k∈Z时,函数f(x)为减函数. 所以函数f(x)的单调递减区间是,k∈Z. (2)由(1)知,f(x)=sin, 又f=, 则sin=,sin=. 因为sin2+cos2=1, 所以cos=±. 又sinα=sin =sincos+cossin, 所以当cos=时, sinα=×+×=; 当cos=-时,sinα=×-×=. 【名师点睛】 在平面向量与三角函数的综合问题中,一方面用平面向量的语言表述三角函数中的问题,如利用向量平行、垂直的条件表述三角函数式之间的关系,利用向量模表述三角函数之间的关系等;另一方面可以利用三角函数的知识解决平面向量问题,在解决此类问题的过程中,只要根据题目的具体要求,在向量和三角函数之间建立起联系,就可以根据向量或者三角函数的知识解决问题. 【锦囊妙计,战胜自我】 平面向量作为解决问题的工具,具有代数形式和几何形式的“双重型”,高考常在平面向量与三角函数的交汇处命题,通过向量运算作为题目条件. 1.在△ABC中,已知D是AB边上一点,若=2,=+λ,则λ等于( ) A. B. C.- D.- 答案 A 解析 在△ABC中,已知D是AB边上一点, ∵=2,=+λ,∴=+=+=+(-)=+,∴λ=. 2.△ABC是边长为2的等边三角形,已知向量a,b满足=2a,=2a+b,则下列结论正确的是( ) A.|b|=1 B.a⊥b C.a·b=1 D.(4a+b)⊥ 答案 D 3.在等腰△ABC中,∠BAC=90°,AB=AC=2,=2,=3,则·的值为( ) A.- B.- C. D. 答案 A 解析 由已知得到·=(+)·(+)=-2+·+·+2,△ABC是等腰直角三角形,∠BAC=90°,AB=AC=2,所以·=-×22+0+0+×22=-,故选A. 4.已知向量a,b满足(a+2b)·(a-b)=-6,且|a|=1,|b|=2,则a与b的夹角为( ) A. B. C. D. 答案 B 解析 设a与b的夹角为θ,∵(a+2b)·(a-b)=-6,且|a|=1,|b|=2,∴1+a·b-8=-6, ∴a·b=1=|a||b|cosθ,∴cosθ=, 又∵θ∈0,π],∴θ=,故选B. 5.已知平面向量a、b(a≠0,a≠b)满足|a|=3,且b与b-a的夹角为30°,则|b|的最大值为( ) A.2B.4C.6D.8 答案 C 解析 令=a,=b,则b-a=-=,如图, ∵b与b-a的夹角为30°,∴∠OBA=30°, ∵|a|=||=3,∴由正弦定理=得,|b|=||=6·sin∠OAB≤6,故选C. 6.若点M是△ABC所在平面内的一点,且满足5=+3,则△ABM与△ABC的面积比值为________. 答案 解析 设AB的中点为D, 由5=+3,得3-3=2-2, 即3=2. 如图所示,故C,M,D三点共线,且=, 也就是△ABM与△ABC对于边AB的两高之比为3∶5, 则△ABM与△ABC的面积比值为. 7.设向量=(5+cosθ,4+sinθ),=(2,0),则||的取值范围是________. 答案 4,6] 解析 ∵=-=(-3-cosθ,-4-sinθ), ∴||2=(-3-cosθ)2+(-4-sinθ)2 =6cosθ+8sinθ+26=10sin(θ+φ)+26, 其中tanφ=, ∴16≤||2≤36,∴4≤||≤6. 8.设向量a=(a1,a2),b=(b1,b2),定义一种向量积a⊗b=(a1b1,a2b2),已知向量m=(2,),n=(,0),点P(x,y)在y=sinx的图象上运动,Q是函数y=f(x)图象上的点,且满足=m⊗+n(其中O为坐标原点),则函数y=f(x)的值域是________. 答案 -,] 9.已知函数f(x)=sinxcosx+sin2x+(x∈R). (1)当x∈时,求函数f(x)的最小值和最大值; (2)设△ABC的内角A,B,C所对的边分别为a,b,c,且c=,f(C)=2,若向量m=(1,a)与向量n=(2,b)共线,求a,b的值. 解 (1)∵函数f(x)=sinxcosx+sin2x+ (x∈R), ∴f(x)=sin2x++ =sin2x-cos2x+1 =sin+1. ∵-≤x≤,∴-≤2x-≤, ∴-≤sin≤1, ∴1-≤sin+1≤2, ∴f(x)的最小值是1-,最大值是2. (2)∵f(C)=sin+1=2, ∴sin=1,∵0查看更多
- 当前文档收益归属上传用户