备战2014高考数学 高频考点归类分析（真题为例）：不等式（选修）

备战2014高考数学 高频考点归类分析（真题为例）：不等式（选修）

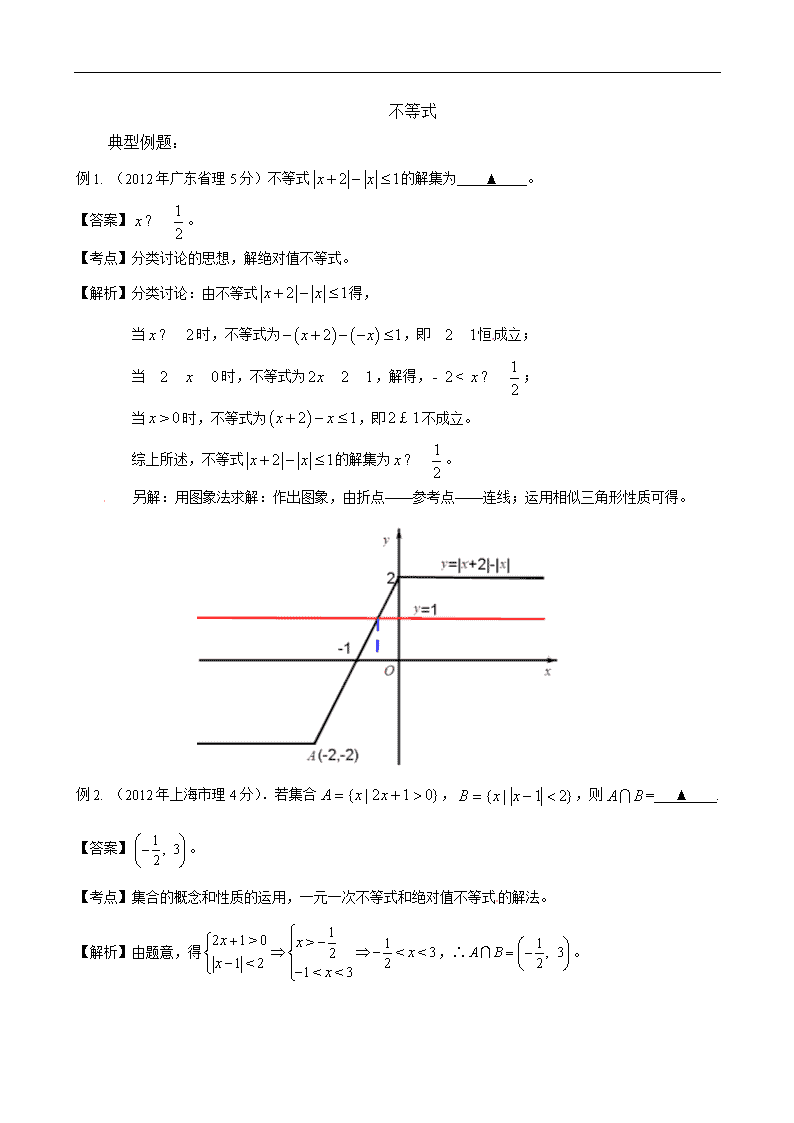
不等式 典型例题： ‎ 例1. （2012年广东省理5分）不等式的解集为　　▲　　。‎ ‎【答案】。‎ ‎【考点】分类讨论的思想，解绝对值不等式。‎ ‎【解析】分类讨论：由不等式得，‎ ‎　　　　当时，不等式为，即恒成立；‎ ‎　　　　当时，不等式为，解得，；‎ 当时，不等式为，即不成立。‎ 综上所述，不等式的解集为。‎ ‎　　　　另解：用图象法求解：作出图象，由折点——参考点——连线；运用相似三角形性质可得。‎ 例2. （2012年上海市理4分）．若集合，，则= ▲ .‎ ‎【答案】。‎ ‎【考点】集合的概念和性质的运用，一元一次不等式和绝对值不等式的解法。‎ ‎【解析】由题意，得，∴。‎ 例3. （2012年天津市理5分）已知集合，集合,且，则 ▲ , ▲ .[来源:Z。xx。k.Com]‎ ‎【答案】，。‎ ‎【考点】集合的交集的运算及其运算性质，绝对值不等式与一元二次不等式的解法 ‎【分析】由题意，可先化简集合，再由集合的形式及直接作出判断，即可得出两个参数的值：‎ ‎∵=,[来源:学_科_网Z_X_X_K]‎ 又∵，画数轴可知，。‎ 例4. （2012年天津市文5分）集合中最小整数为 ▲ ‎ ‎【答案】。‎ ‎【考点】绝对值不等式的解法。‎ ‎【分析】∵不等式，即，，∴集合。‎ ‎ ∴集合中最小的整数为。‎ 例5. （2012年山东省理4分）若不等式的解集为，则实数= ▲ 。[来源:Zxxk.Com]‎ ‎【答案】2。‎ ‎【考点】绝对值不等式的性质。‎ ‎【解析】由可得，即，而，所以。‎ 例6. （2012年江西省理5分）在实数范围内，不等式的解集为 ▲ 。‎ ‎【答案】。‎ ‎【考点】绝对值不等式的解法，转化与划归、分类讨论的数学思想的应用。‎ ‎【解析】原不等式可化为①或②或③，‎ 由①得；由②得；由③得。‎ ‎∴原不等式的解集为。‎ 例7. （2012年陕西省文5分）若存在实数使成立，则实数的取值范围是 ▲ ‎ ‎【答案】。‎ ‎【考点】绝对值不等式的性质及其运用。‎ ‎【解析】由题意知左边的最小值小于或等于3，根据不等式的性质，得 ‎，解得，。[来源:Z.xx.k.Com]‎ 例8. （2012年湖南省理5分）不等式的解集为 ▲ ‎ ‎【答案】。‎ ‎【考点】解绝对值不等式。‎ ‎【解析】令，则由得的解集为。‎ 例9. （2012年全国课标卷文5分）已知函数 ‎(Ｉ)当时，求不等式的解集；‎ ‎(Ⅱ)若的解集包含，求的取值范围。‎ ‎【答案】解：（1）当时，由得 ‎ ∴ 或或。‎ ‎ 解得 或。[来源:学科网ZXXK]‎ ‎ (Ⅱ)原命题即在上恒成立，‎ ‎ ∴在上恒成立，即在上恒成立。‎ ‎ ∴。‎ ‎【考点】绝对值不等式的解法。‎ ‎【解析】(Ｉ)分段求解即可。‎ ‎ (Ⅱ)对于，把作未知求解。‎ 例10. （2012年辽宁省文10分）已知，不等式的解集为｝。[来源:学科网ZXXK]‎ ‎ (Ⅰ)求a的值；‎ ‎ (Ⅱ)若恒成立，求k的取值范围。‎ ‎【答案】解：（I）由得。‎ ‎ 又∵不等式的解集为｝，‎ ‎ ∴当时，不合题意；‎ ‎ 当时，，得。‎ ‎(Ⅱ)由（I）得。记。‎ ‎ ∴。∴。‎ ‎【考点】分段函数、不等式的基本性质、绝对值不等式及其运用，分类讨论思想的应用。‎ ‎【解析】（I）针对的取值情况进行讨论即可。‎ ‎ (Ⅱ) 针对的正负进行讨论从而用分段函数表示，进而求出k的取值范围。‎ 例11.（2012年江苏省10分）已知实数x，y满足：求证：．‎ ‎【答案】证明：∵，‎ ‎ 由题设∴。∴。 ‎ ‎【考点】绝对值不等式的基本知识。‎ ‎【解析】根据绝对值不等式的性质求证。‎