2019届高考数学（文）备战冲刺预测卷2（二）

2019届高考数学（文）备战冲刺预测卷2（二）

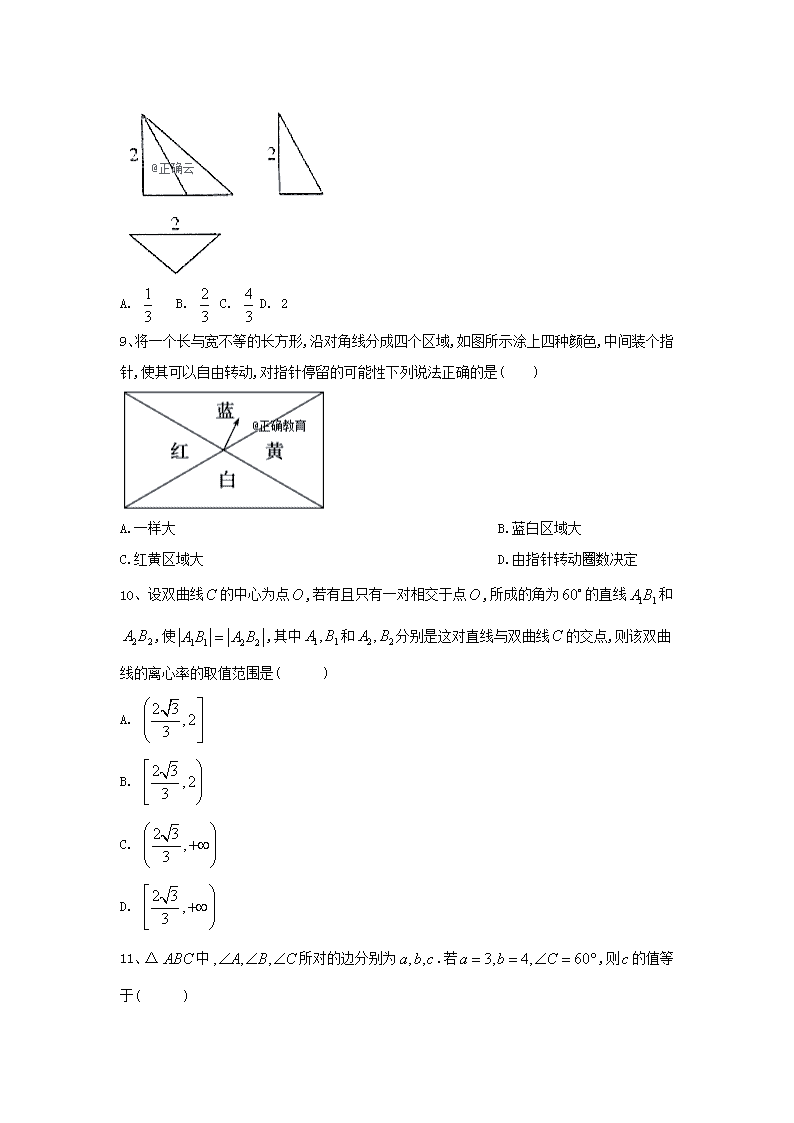
备战冲刺预测卷（二）‎ ‎1、已知为虚数单位,则 (   )‎ A. B. C. D. ‎ ‎2、设集合,则 (   ).‎ A. B. C. D. ‎ ‎3、下列函数中,既是偶函数又是上的增函数的为(   )‎ A. B. C. D. ‎ ‎4、已知条件,条件直线与直线平行,则是的(   )‎ A.充要条件                     B.必要不充分条件 C.充分不必要条件                  D.既不充分也不必要条件 ‎5、等比数列中,,则数列的公比为(   )‎ A. B. ‎ ‎ C. 或 D. ‎ ‎6、如图是为了求出满足的最小偶数,那么在和两个空白框中,可以分别填入(   )‎ A. 和 B. 和 C. 和 D. 和 ‎7、设实数满足不等式组,则的取值范围是(   )‎ A. B. C. D. ‎ ‎8、某三棱锥的三视图如图所示，其俯视图是一个等腰直角三角形，则此三棱锥的体积为（ ） ‎ A. B. C. D. 2‎ ‎9、将一个长与宽不等的长方形,沿对角线分成四个区域,如图所示涂上四种颜色,中间装个指针,使其可以自由转动,对指针停留的可能性下列说法正确的是(   )‎ A.一样大                       B.蓝白区域大 C.红黄区域大                     D.由指针转动圈数决定 ‎10、设双曲线的中心为点,若有且只有一对相交于点,所成的角为的直线和,使,其中和分别是这对直线与双曲线的交点,则该双曲线的离心率的取值范围是(    )‎ A. B. C. D. ‎ ‎11、△中所对的边分别为.若,则的值等于(   )‎ A. B. C. D. ‎ ‎12、方程的根所在的一个区间是(   )‎ A. B. C. D.     ‎ ‎13、设向量满足，则____． ‎ ‎14、已知,且满足,则的最大值为__________.‎ ‎15、若圆上总存在到原点的距离为的点,则实数的取值范围是__________‎ ‎16、函数的最大值是__________.‎ ‎17、在公差为的等差数列中,已知,且,,成等比数列. 1.求,; 2.若,求.‎ ‎18、如图,正三角形的边长为2,分别为边的中点,将沿折起,使点C在平面上的射影恰好为的交点为的三等分点且靠近点C,,连接.‎ ‎1.求证:平面平面;‎ ‎2.求三棱锥的体积.‎ ‎19、从甲乙两部门中各任选10名员工进行职业技能测试，测试成绩（单位：分）数据的茎叶图如图1所示：‎ ‎（1）分别求出甲、乙两组数据的中位数，并从甲组数据频率分布直方图如图2所示中求的值；‎ ‎（2）从甲、乙两组数据中各任取一个，求所取两数之差的绝对值大于20的概率.‎ ‎20、已知椭圆的一个顶点为,焦点在轴上.若右焦点到直线的距离为.‎ ‎1.求椭圆的方程;‎ ‎2.设椭圆与直线相交于不同的两点、.当时,求的取值范围.‎ ‎21、设,函数,函数. 1.当时,求函数的零点个数; 2.若函数与函数的图象分别位于直线的两侧,求的取值集合; 3.对于,求的最小值.‎ ‎22、在平面直角坐标系中,曲线的参数方程为 (为参数)以平面直角坐标系的原点为极点, 轴的非负半轴为极轴建立极坐标系,直线的极坐标方程为 ‎1.求曲线的极坐标方程 ‎2.设和交点的交点为,,求的面积 ‎23、[选修4-5：不等式选讲]‎ 已知函数.‎ ‎1.求的解集；‎ ‎2.若关于x的不等式能成立，求实数m的取值范围. ‎ 答案 ‎1.B 解析：因为,‎ ‎2.A 解析：因为集合 所以 又因为 所以,故选 ‎3.D 解析：根据题意,依次分析选项:对于A, 为一次函数,不是偶函数,不符合题意;‎ 对于B, ,在上是减函数,不符合题意;‎ 对于C, ,为反比例函数,不是偶函数,不符合题意;‎ 对于D, 为开口向下的二次函数,且其对称轴为轴,则既是偶函数又是上的增函数,符合题意;故选:D.‎ ‎4.C ‎5.A ‎6.D 解析：根据程序框图求的最小正偶数可知,判断框中应填: ,根据初始值为偶数可知.‎ ‎7.C 解析：作出可行域如图阴影部分所示,把目标函数变形为,‎ 由图可知当目标直线过点时取得最小值,目标直线过点时取最大值,‎ 分别代入可得,‎ 所以.‎ ‎8.B 解析：由三视图可知，该三棱锥的一条侧棱与底面垂直，且三棱锥的高为2，底面等腰直角三角形的斜边长是2，利用锥体的体积公式可得结果.‎ ‎9.B 解析：指针停留在哪个区域的可能性大,即表明该区域的张角大,显然,蓝白区域大.‎ ‎10.A 解析：设双曲线的焦点在轴上,则由题意知该双曲线的一条渐近线的斜率必须满足,易知,所以,,即有.又双曲线的离心率为,所以.‎ ‎11.C ‎12.B ‎13.7‎ ‎14.3‎ 解析：解法一:由得,当且仅当时取等号; 解法二:由得,由得,∴.当时, .‎ ‎15.‎ 解析：∵圆的圆心到原点的距离为,半径,且圆上总存在到原点的距离为的点,∴,∴,解得或∴实数的取值范围是 ‎16.1‎ 解析：由于,‎ 而则,故当,即时, ‎ ‎17.1. 或; 或 2. ‎ 解析：1.由题意,得, ∴, ∴或. ∴或. 2.设数列的前项和为. ∵,由1得,, 则当时, . 当时, . 综上所述, .‎ ‎18.1.由题意得,,‎ 易知,且,∴,∴.‎ ‎∵,,,‎ ‎∴平面平面.‎ ‎2.连接,过点F作交于点H,易知.‎ ‎∵,∴,,‎ ‎∴,‎ ‎∴.‎ ‎19.（1）根据茎叶图得甲部门数据的中位数是，乙部门数据的中位数是；‎ 因为甲部门的成绩在的频率为，所以，同理，.‎ ‎（2）从“甲、乙两组数据中各任取一个”的所有可能情况是：‎ ‎，，……共有100种；‎ 其中所取“两数之差的绝对值大于”的情况是： ，，，，，，，，，，，，，，，共有种，‎ 故所求的概率为 ．‎ 解析： ‎ ‎20.1.依题意可设椭圆方程为,则右焦点由题设 解得故所求椭圆的方程为 2.设为弦的中点,由 得 由于直线与椭圆有两个交点,∴△>0,即①‎ ‎∴从而 ‎∴又,‎ 则即②‎ 把②代入①得解得由②得解得故所求的取范围是 ‎21.1.当时, .‎ 由得;由得.‎ 所以函数在上单调递增,在上单调递减,‎ 因为,‎ 所以函数在上存在一个零点;‎ 当时, 恒成立,‎ 所以函数在上不存在零点.‎ 综上得函数在上存在唯一一个零点. 2.由函数求导,得,‎ 由,得;由,得,‎ 所以函数在上单调递增,在上单调递减,‎ 则当时,函数有最大值;‎ 由函数求导,得,‎ 由得;由得.‎ 所以函数在上单调递减,在上单调递增,‎ 则当时,函数有最小值;‎ 因为,函数的最大值,‎ 即函数在直线的下方,‎ 故函数在直线的上方,‎ 所以,解得.‎ 所以的取值集合为. 3.对的最小值等价于,‎ 当时, ;‎ 当时, ;‎ 因为,‎ 所以的最小值为 ‎22.1.曲线的参数方程为 (为参数)消去参数的的直角坐标方程为: 所以的极坐标方程为  2.解方程组有得 ∴或 当时, ,当时, ∴和交点的极坐标∴故的面积 ‎23.1. ，‎ 故的解集为.‎ ‎2.由能成立，‎ 得能成立，‎ 即能成立，‎ 令，则能成立，‎ 由1知，，又∵，‎ ‎∴，‎ ‎∴实数m的取值范围：.‎ 解析： ‎