2019年高考理科数学考前30天--计算题专训（十八）

2019年高考理科数学考前30天--计算题专训（十八）

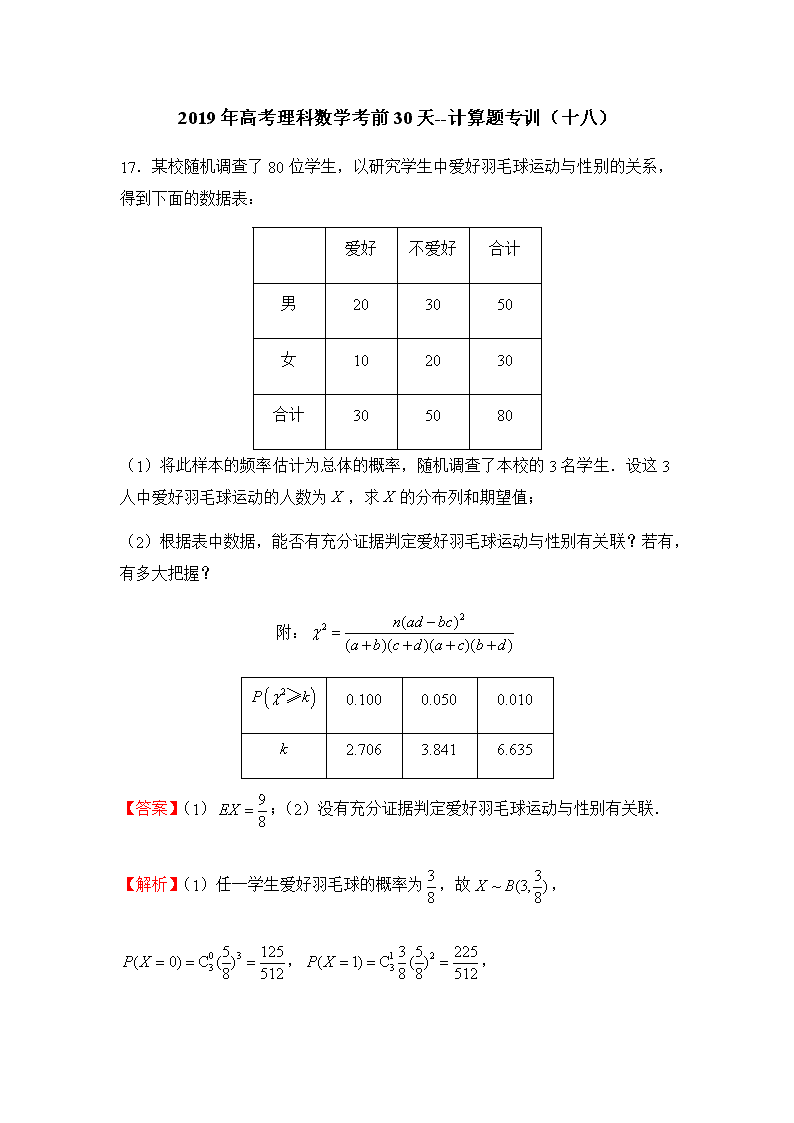
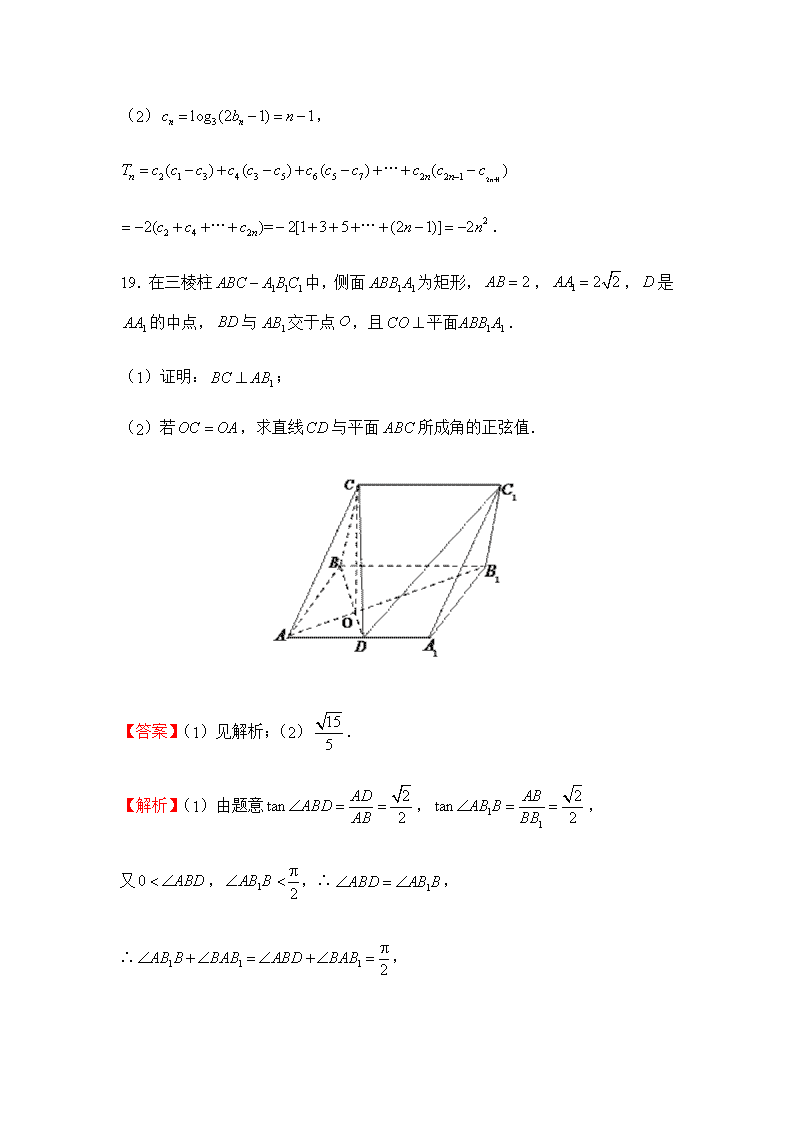
‎2019年高考理科数学考前30天--计算题专训（十八）‎ ‎17．某校随机调查了80位学生，以研究学生中爱好羽毛球运动与性别的关系，得到下面的数据表：‎ 爱好 不爱好 合计 男 ‎20‎ ‎30‎ ‎50‎ 女 ‎10‎ ‎20‎ ‎30‎ 合计 ‎30‎ ‎50‎ ‎80‎ ‎（1）将此样本的频率估计为总体的概率，随机调查了本校的3名学生．设这3人中爱好羽毛球运动的人数为，求的分布列和期望值；‎ ‎（2）根据表中数据，能否有充分证据判定爱好羽毛球运动与性别有关联？若有，有多大把握？‎ 附：‎ ‎0.100‎ ‎0.050‎ ‎0.010‎ ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎【答案】（1）；（2）没有充分证据判定爱好羽毛球运动与性别有关联．‎ ‎【解析】（1）任一学生爱好羽毛球的概率为，故，‎ ‎，，‎ ‎，，‎ 的分布列为：‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎∴．‎ ‎（2），故没有充分证据判定爱好羽毛球运动与性别有关联．‎ ‎18．已知数列为等差数列，首项，公差．若成等比数列，且．‎ ‎（1）求数列的通项公式；‎ ‎（2）设，求和．‎ ‎【答案】（1）；（2）．‎ ‎【解析】（1），，‎ ‎，，∴，，∴．‎ ‎（2），‎ ‎．‎ ‎19．在三棱柱中，侧面为矩形，，，是的中点，与交于点，且．‎ ‎（1）证明：；‎ ‎（2）若，求直线与平面所成角的正弦值．‎ ‎【答案】（1）见解析；（2）．‎ ‎【解析】（1）由题意，，‎ 又，，∴，‎ ‎∴，‎ ‎∴，∴，又，∴，‎ ‎∵与交于点，∴，又，‎ ‎∴．‎ ‎（2）如图，分别以，，所在直线为，，轴，以为坐标原点，建立如图所示的空间直角坐标系，则，，，，，，，‎ 设平面的法向量为，‎ 则，即，令，则，，所以．‎ 设直线与平面所成角为，则：‎ ‎．‎ ‎20．已知抛物线的焦点为，过的直线交抛物线于点，，当直线的倾斜角是时，的中垂线交轴于点．‎ ‎（1）求的值；‎ ‎（2）以为直径的圆交轴于点，，记劣弧的长度为，当直线绕旋转时，求的最大值．‎ ‎【答案】（1）；（2）．‎ ‎【解析】（1），当直线的倾斜角为时，直线的方程为，‎ 设，，得，‎ ‎，，得中点为，‎ 中垂线为，代入得，．‎ ‎（2）设的方程为，代入得，‎ ‎，中点为，‎ 令，，，‎ 到轴的距离，，‎ 当时，取最小值，的最大值为，故的最大值为．‎ ‎21．已知函数，，，三个函数的定义域均为集合．‎ ‎（1）若恒成立，满足条件的实数组成的集合为，试判断集合与的关系，并说明理由；‎ ‎（2）记，是否存在，使得对任意的实数，函数有且仅有两个零点？若存在，求出满足条件的最小正整数；若不存在，说明理由．（以下数据供参考：，）‎ ‎【答案】（1），；（2）．‎ ‎【解析】（1），，‎ ‎．‎ 易知在上递减，．‎ 存在，使得，函数在递增，在递减，．‎ 由得，，，．‎ ‎（2）令，，．‎ ‎，，由于，，，‎ ‎，由零点存在性定理可知：，函数在定义域内有且仅有一个零点．‎ ‎，，，，，同理可知，函数在定义域内有且仅有一个零点．‎ 假设存在使得，，‎ 消得，‎ 令，，‎ 递增，，，‎ ‎，‎ 此时，所以满足条件的最小整数