高三数学二轮复习12_2函数与方程及函数的应用课时巩固过关练理新人教版
课时巩固过关练 四 函数与方程及函数的应用
(35 分钟 55 分)
一、选择题(每小题 5 分,共 20 分)
1.(2016·荆州一模)函数 f(x)=lnx- 的零点所在的区间是 ( )
A.(1,2) B.(2,3)
C.(3,4) D.(e,+∞)
【解析】选 B.因为 f(x)=lnx- ,
则函数 f(x)在(0,+∞)上单调递增,
因为 f(2)=ln2-1<0,f(3)=ln3- >0,
所以 f(2)f(3)<0,
所以在区间(2,3)内函数 f(x)存在零点.
2.(2016·张掖一模)已知函数 f(x)=ex+x,g(x)=lnx+x,h(x)=x- 的零点依次为 a,b,c,则
( )
A.c
0,
且函数 f(x)是增函数,因此函数 f(x)的零点在区间(0,1)内,
即 00,
且函数 g(x)在(0,+∞)上单调递增.
所以函数 g(x)的零点在区间(1,2)内,
即 1f(1)>0>g(m).
3.(2016·郑州一模)已知函数 f(x)=ax+x-b 的零点 x0∈(n,n+1)(n∈Z),其中常数 a,b 满足
00,进而可得 n 的值.
【解析】选 D.由题意得函数 f(x)=ax+x-b 为增函数,常数 a,b 满足 00,
所以函数 f(x)=ax+x-b 在(-1,0)内有一个零点,
故 n=-1.
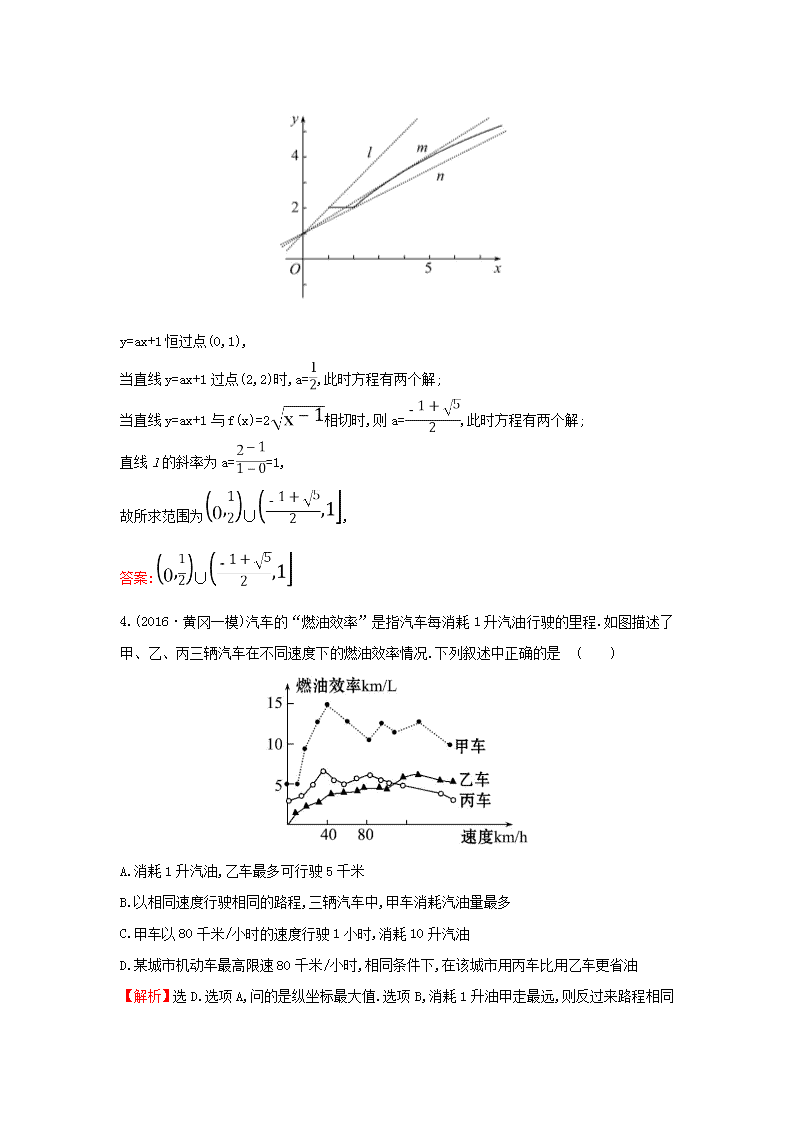
【加固训练】(2016·沈阳一模)已知函数 f(x)= 若方程 f(x)=ax+1 恰有
一个解,则实数 a 的取值范围为________.
【解析】作函数 f(x)= 与 y=ax+1 的图象如图,
y=ax+1 恒过点(0,1),
当直线 y=ax+1 过点(2,2)时,a= ,此时方程有两个解;
当直线 y=ax+1 与 f(x)=2 相切时,则 a= ,此时方程有两个解;
直线 l 的斜率为 a= =1,
故所求范围为 ∪ ,
答案: ∪
4.(2016·黄冈一模)汽车的“燃油效率”是指汽车每消耗 1 升汽油行驶的里程.如图描述了
甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是 ( )
A.消耗 1 升汽油,乙车最多可行驶 5 千米
B.以相同速度行驶相同的路程,三辆汽车中,甲车消耗汽油量最多
C.甲车以 80 千米/小时的速度行驶 1 小时,消耗 10 升汽油
D.某城市机动车最高限速 80 千米/小时,相同条件下,在该城市用丙车比用乙车更省油
【解析】选 D.选项 A,问的是纵坐标最大值.选项 B,消耗 1 升油甲走最远,则反过来路程相同
甲最省油.选项 C,此时甲走过了 80 千米,消耗 8 升汽油.选项 D,80 千米/小时以下丙“燃油
效率”更高,更省油.
二、填空题(每小题 5 分,共 10 分)
5.若关于 x 的方程 4sin2x-msinx+1=0 在(0,π)内有两个不同的实数根,则实数 m 的取值范围
为______.
【解析】设 sinx=t,则 05.
答案:m=4 或 m>5
6.(2016·石嘴山二模)对于实数 a,b,定义运算“⊗ ”:a⊗ b= 设 f(x)=(2x-1)
⊗ (x-1),且关于 x 的方程 f(x)-m=0 恰有三个互不相等的实数根,则实数 m 的取值范围是
________.
【解析】由 2x-1≤x-1 可得 x≤0,由 2x-1>x-1 可得 x>0.所以根据题意得 f(x)
=
即 f(x)= 画出函数的图象,从图象上观察当关于 x 的方程 f(x)=m(m∈R)
恰有三个互不相等的实数根时,
函数的图象和直线 y=m 有三个不同的交点,再根据函数的极大值为 f = ,
可得 m 的取值范围是 .
答案:
【加固练习】(2016·广州二模)设函数 f(x)的定义域为 R,f(-x)=f(x), f(x)=f(2-x),当 x
∈[0,1]时,f(x)=x3,则函数 g(x)=|cos(πx)|-f(x)在区间 上的所有零点的和为
________.
【解析】因为 f(-x)=f(x),f(x)=f(2-x),
所以 f(-x)=f(2-x),所以 f(x)的周期为 2.
画出 y=f(x)和 y=|cos(πx)|的图象,
由图可知,g(x)共有 5 个零点,
其中 x1+x2=0,x4=1,x3+x5=2.
所以所有零点的和为 3.
答案:3
三、解答题(7 题 12 分,8 题 13 分,共 25 分)
7.(2016 · 衡 水 一 模 ) 已 知 函 数 f(x)= 若 关 于 x 的 不 等 式
[f(x)]2+af(x)-b2<0 恰有 1 个整数解,求实数 a 的最大值.
【解析】结合函数 f(x)= 的图象,
①当 b=0 时,[f(x)]2+af(x)-b2<0 化为[f(x)]2+af(x)<0,
当 a>0 时,-a3,
a≤0 不必考虑.
②当 b≠0 时,对于[f(x)]2+af(x)-b2<0,
Δ=a2+4b2>0,
解得: 0,因为关于 x 的不等式[f(x)]2+af(x)-b2<0 恰有 1 个整数解,所以 f(x)=0,
则 <0< ,
由于 f(x)=0 时,不等式的解集中含有多于一个整数解(例如,0,2),舍去.
综上可得:a 的最大值为 8.
【加固训练】已知函数f(x)=x2+ax+b(a,b∈R),记 M(a,b)是|f(x)|在区间[-1,1]上的最大值.
(1)证明:当|a|≥2 时,M(a,b)≥2.
(2)当 a,b 满足 M(a,b)≤2,求|a|+|b|的最大值.
【解析】(1)因为 f(x)=x2+ax+b(a,b∈R),
= +b- ,
所以对称轴为直线方程 x=- ,
由 a≥2 得:- ≤-1,
所以 f(x)在[-1,1]上单调递增,
所以 M(a,b)等于|f(1)|与|f(-1)|两者的最大值.
当 a≥2 时,由 f(1)-f(-1)=2a≥4,
可知|f(1)|与|f(-1)|两者的最大值大于等于 2;
当 a≤-2 时,由 f(1)-f(-1)=2a≤-4,
可知|f(1)|与|f(-1)|两者的最大值大于等于 2.
综上可知:当|a|≥2 时,M(a,b)≥2.
(2)由 M(a,b)≤2 可得|1+a+b|=|f(1)|≤2,
|1-a+b|=|f(-1)|≤2,所以|a-b|≤3,|a+b|≤3.
因为|a|+|b|=
所以|a|+|b|≤3.
当 a=2,b=-1 时,|a|+|b|=3,
且|x2+ax+b|在[-1,1]上的最大值为 2,
即 M(2,-1)=2,所以|a|+|b|的最大值为 3.
8.(2016·唐山一模)有一种新型的洗衣液,去污速度特别快.已知每投放 k(1≤k≤4,且 k∈R)
个单位的洗衣液在一定量水的洗衣机中,它在水中释放在浓度 y(克/升)随着时间 x(分钟)变
化的函数关系式近似为 y=k·f(x),其中 f(x)= 若多次投放,则某一
时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水
中冼衣液的浓度不低于 4 克/升时,它才能起到有效去污的作用.
(1)若只投放一次 k 个单位的洗衣液,当两分钟时水中洗衣液的浓度为 3 克/升,求 k 的值.
(2)若只投放一次 4 个单位的洗衣液,则有效去污时间可达几分钟?
(3)若第一次投放 2 个单位的洗衣液,10 分钟后再投放 1 个单位的洗衣液,则在第 12 分钟时
洗衣液是否还能起到有效去污的作用?请说明理由.
【解析】(1)由题意知 k =3,
所以 k=1.
(2)因为 k=4,
所以 y=
当 0≤x≤4 时,由 -4≥4,
解得-4≤x<8,所以 0≤x≤4.
当 44,
所以在第 12 分钟时还能起到有效去污的作用.
(30 分钟 55 分)
一、选择题(每小题 5 分,共 20 分)
1.下列函数中,在(-1,1)内有零点且单调递增的是 ( )
A.y=log2x B.y=2x-1
C.y=x2-2 D.y=-x3
【解析】选 B.y=log2x 在(-1,1)内有没有意义的情况,故 A 不对;
y=x2-2 在(-1,0)单调递减,故 C 不对;
y=-x3 在(-1,1)单调递减,故 D 不对.
因为 y=2x-1,单调递增,f(-1)<0,f(1)>0,
所以在(-1,1)内存在零点.
【加固训练】已知函数 f(x)=ax2-ex,f′(-1)=-4,则函数 y=f(x)的零点所在的区间是
( )
A.(-3,-2) B.(-1,0)
C.(0,1) D.(4,5)
【解析】选 B.因为 f(x)=ax2-ex,f′(-1)=-4,
所以-2a-e-1=-4,
所以 a=2- ,
所以 f(x)= x2-ex,
所以 f(-1)=2- >0,f(0)=-1<0,
所以函数 y=f(x)的零点所在的区间是(-1,0).
2.已知函数 f(x)= 则 f(x)=log0.6(x+1)的根的个数为 ( )
A.0 B.1 C.2 D.3
【解析】选 C.f(x)=log0.6(x+1)的根的个数,
即函数 y=f(x)与 y=log0.6(x+1)图象交点的个数,
在同一坐标系中画出两个函数的图象如图所示:
由图可得两个函数图象共有 2 个交点,
故方程 f(x)=log0.6(x+1)有两个根.
3.已知函数 f(x)= 若|f(x)|≥ax,则 a 的取值范围是 ( )
A.(-∞,0] B.(-∞,1]
C.[-3,0] D.[-3,1]
【解题导引】①当 x>0 时,根据 ln(x+1)>0 恒成立,求得 a≤0.
②当 x≤0 时,可得 x2-3x≥ax,求得 a 的范围.再把这两个 a 的取值范围取交集,可得答案.
【解析】选 C.当 x>0 时,根据 ln(x+1)>0 恒成立,
则此时 a≤0.
当 x≤0 时,根据-x2+3x 的取值为(-∞,0],
|f(x)|=x2-3x≥ax,x=0 时,左边=右边,a 取任意值.
当 x<0 时,有 a≥x-3,即 a≥-3.
综上可得,a 的取值为[-3,0].
4.若函数 f(x)=2exln(x+m)+ex-2 存在正的零点,则实数 m 的取值范围为 ( )
A.(-∞, ) B.( ,+∞)
C.(-∞,e) D.(e,+∞)
【解析】选 A.令 2exln(x+m)+ex-2=0,
所以 ln(x+m)= - .
因为 y= - 过点 ,且为单调减函数.
所以 x>0 时,y= - < .
问题等价于 ln(x+m)< ,x>0 恒成立.
因为 y=ln(x+m)在(0,+∞)上为增函数,
所以 lnm< ,m< .
【加固训练】设 f(x)是定义在 R 上的偶函数,f(x)+f(2-x)=0.当 x∈[0,1]时,f(x)=x2-1,若
关于 x 的方程 f(x)-kx=0 恰有三个不同的实数解,则正实数 k 的取值范围是 ( )
A.(5-2 ,4- )
B.(8-2 ,4-2 )
C.(5-2 ,4-2 )
D.(8-2 ,4- )
【解题导引】根据函数奇偶性和对称性求出函数的周期,以及函数的解析式,利用函数与方程
之间的关系,转化为函数 f(x)与 y=kx 有三个不同的交点,利用数形结合,以及直线和抛物线
相切的等价条件,利用判别式Δ=0,进行求解即可.
【解析】选 B.因为 f(x)是定义在 R 上的偶函数,f(x)+f(2-x)=0.
所以 f(x)=-f(2-x)=-f(x-2),
即 f(x+2)=-f(x),
则 f(x+4)=-f(x+2)=f(x),
即函数为周期是 4 的周期函数,
若 x∈[-1,0],则-x∈[0,1],
此时 f(-x)=x2-1=f(x),
即 f(x)=x2-1,x∈[-1,0],
综上,f(x)=x2-1,x∈[-1,1],
若 x∈[-2,-1],则 x+2∈[0,1],
则由 f(x+2)=-f(x),
得 f(x)=-f(x+2)=-[(x+2)2-1]=1-(x+2)2,
x∈[-2,-1],
若 x∈[1,2],则-x∈[-2,-1],
则 f(-x)=1-(-x+2)2=1-(x-2)2=f(x),
即 f(x)=1-(x-2)2,x∈[1,2],
即函数在一个周期[-2,2]上的解析式为
f(x)=
若关于 x 的方程 f(x)-kx=0 恰有三个不同的实数解,等价为 f(x)=kx 恰有三个不同的实数解,
即函数 f(x)与 y=kx 有三个不同的交点,作出函数 f(x)和 y=kx 的图象如图:
当 x∈[1,2]时,由 f(x)=1-(x-2)2=kx,
得 x2+(k-4)x+3=0,
由判别式Δ=(k-4)2-12=0,得 k-4=±2 ,
即 k=4±2 ,
由 1<- <2,解得 0”“=”或“<”)
【解析】因为已知 x0 是 f(x)= + 的一个零点,x1∈(-∞,x0),x2∈(x0,0),
可令 h(x)= ,g(x)=- ,如图:
当 0>x>x0 时,g(x)>h(x),h(x)-g(x)= + <0;
当 x0;
因为 x1∈(-∞,x0),x2∈(x0,0),
所以 f(x1)>0,f(x2)<0.
答案:> <
【加固训练】已知偶函数 f(x)满足 f(x)-f(x+2)=0,且当 x∈[0,1]时,f(x)=x· ex,若在区间
[-1,3]内,函数 g(x)=f(x)-kx-2k 有且仅有 3 个零点,则实数 k 的取值范围是________.
【解析】因为 f(x)-f(x+2)=0,
所以 f(x)=f(x+2),即函数的周期是 2,
因为当 x∈[0,1]时,f(x)=x·ex,
所以根据增函数的性质可知,
此时函数 f(x)单调递增,且 f(0)=0,f(1)=e,所以当 x∈[-1,0]时,f(x)=f(-x)=-x·e-x,
令 g(x)=f(x)-kx-2k=0,得到 f(x)=k(x+2),
作出两个函数 f(x)和 y=k(x+2)在[-1,3]上的图象,
由图象可知当 x=1 时,f(1)=e,
当 x=3 时,f(3)=f(1)=e,
即 B(1,e),C(3,e),当直线 y=k(x+2)经过点 B(1,e)时,此时两个函数有 2 个交点,此时 e=3k,
解得 k= ,
直线 y=k(x+2)经过点 C(3,e)时,
此时两个函数有 4 个交点,
此时 e=5k,解得 k= ,
所以要想使函数 g(x)=f(x)-kx-2k 有且仅有 3 个零点,
则直线 y=k(x+2)应该位于直线 AB 和 AC 之间,
所以此时直线的斜率 k 满足 0,
即函数 f(t)单调递增.
由题意可知 f(x-2)=-2,f(y-2)=2,
即 f(x-2)+f(y-2)=2-2=0,
即 f(x-2)=-f(y-2)=f(2-y),
因为函数 f(t)单调递增,
所以 x-2=2-y,即 x+y=4.
8.已知函数 y=f(x),若在定义域内存在 x0,使得 f(-x0)=-f(x0)成立,则称 x0 为函数 f(x)的局
部对称点.
(1)若 a∈R 且 a≠0,证明:函数 f(x)=ax2+x-a 必有局部对称点.
(2)若函数 f(x)=2x+b 在区间[-1,2]内有局部对称点,求实数 b 的取值范围.
(3)若函数 f(x)=4x-m·2x+1+m2-3 在 R 上有局部对称点,求实数 m 的取值范围.
【解析】(1)由 f(x)=ax2+x-a 得 f(-x)=ax2-x-a,
代入 f(-x)=-f(x)得 ax2+x-a+ax2-x-a=0,
得到关于 x 的方程 ax2-a=0(a≠0),
其中Δ=4a2,由于 a∈R 且 a≠0,
所以Δ>0 恒成立,
所以函数 f(x)=ax2+x-a 必有局部对称点.
(2)f(x)=2x+b 在区间[-1,2]内有局部对称点,
所以方程 2x+2-x+2b=0 在区间[-1,2]上有解,
于是-2b=2x+2-x,
设 t=2x, ≤t≤4,
所以-2b=t+ ,其中 2≤t+ ≤ ,
所以- ≤b≤-1.
(3)因为 f(-x)=4-x-m·2-x+1+m2-3,
由 f(-x)=-f(x),所以 4-x-m·2-x+1+m2-3=-(4x-m·2x+1+m2-3),
于是 4x+4-x-2m(2x+2-x)+2(m2-3)=0…(*)在 R 上有解,
令 t=2x+2-x(t≥2),则 4x+4-x=t2-2,
所以方程(*)变为 t2-2mt+2m2-8=0 在区间[2,+∞)内有解,需满足条件:
即
化简得 1- ≤m≤2 .