中考数学专题复习练习：勾股定理

中考数学专题复习练习：勾股定理

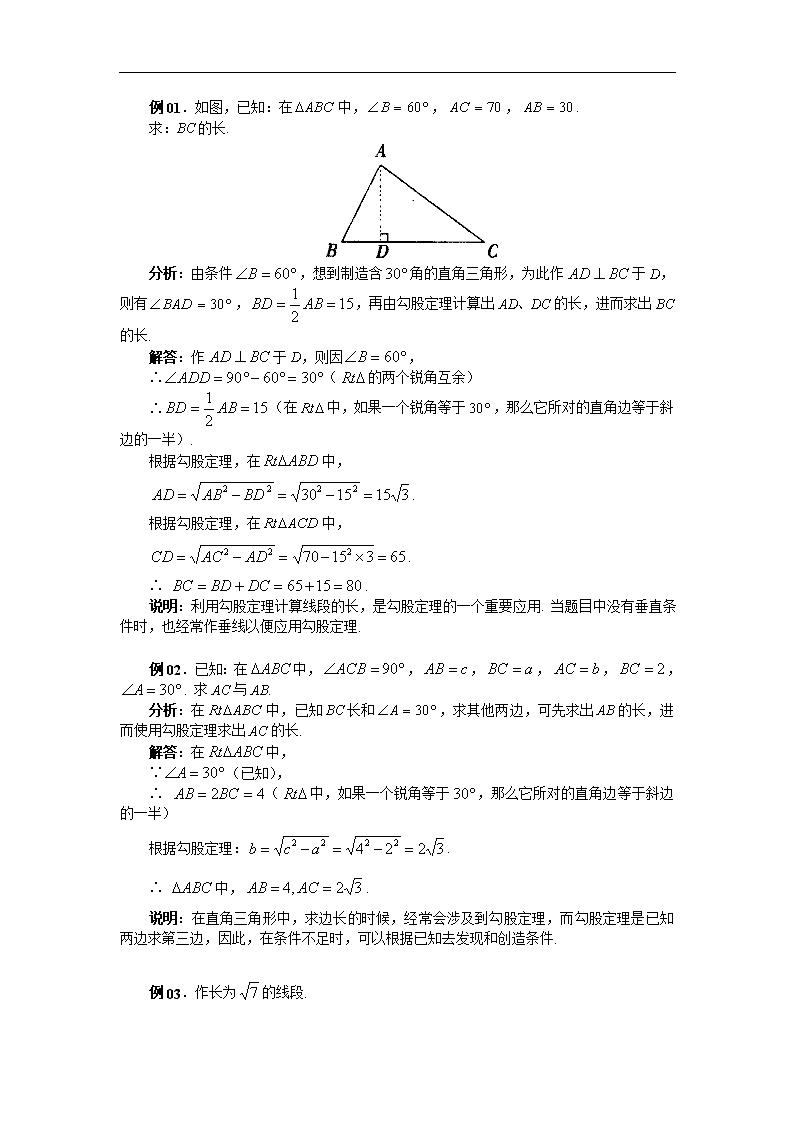
例01．如图，已知：在中，，，. ‎ 求：BC的长. ‎ 分析：由条件，想到制造含角的直角三角形，为此作于D，则有，，再由勾股定理计算出AD、DC的长，进而求出BC的长. ‎ 解答：作于D，则因，‎ ‎∴（的两个锐角互余）‎ ‎∴（在中，如果一个锐角等于，那么它所对的直角边等于斜边的一半）. ‎ 根据勾股定理，在中，‎ ‎. ‎ 根据勾股定理，在中，‎ ‎. ‎ ‎∴ . ‎ 说明：利用勾股定理计算线段的长，是勾股定理的一个重要应用. 当题目中没有垂直条件时，也经常作垂线以便应用勾股定理. ‎ 例02．已知：在中，，，，，，. 求AC与AB. ‎ 分析：在中，已知BC长和，求其他两边，可先求出AB的长，进而使用勾股定理求出AC的长. ‎ 解答：在中，‎ ‎∵（已知），‎ ‎∴ （中，如果一个锐角等于，那么它所对的直角边等于斜边的一半）‎ 根据勾股定理：. ‎ ‎∴ 中，. ‎ 说明：在直角三角形中，求边长的时候，经常会涉及到勾股定理，而勾股定理是已知两边求第三边，因此，在条件不足时，可以根据已知去发现和创造条件. ‎ 例03．作长为的线段. ‎ 分析：根据勾股定理. 即斜边长为4，一条直角边为3的直角三角形的另一条直角边就是. ‎ 作法：1．作长为3的直角边AC，过C作，‎ ‎2．以A为圆心，4为半径画弧交CD于B. ‎ 连结AB，则BC即为所求. 如图. ‎ 证明：在中，根据勾股定理：‎ ‎，‎ ‎∴ . ‎ 说明：也可按书中作法，由两条直角边都为1 的直角三角形先作出，然后依次作出，2，，，最后作出. 但这样较繁. 可以先作出与相近且能一步作出的线段. 如先作，再作，，也可先作，再作. ‎ 例04．如图，已知：，，，. ‎ 求：BC的长. ‎ 分析：因为是等腰直角三角形，，根据勾股定理知，即，所以只需求AB的长. AB的长可在中求出. 在直角三角形ABD中，，所以. 那么可根据勾股定理，求出AB的长. ‎ 解答：∵，（已知），‎ ‎∴ . （在直角三角形中，如果一个锐角等于 ‎，那么它所对的直角边等于斜边的一半）. ‎ 根据勾股定理：在中，‎ ‎∴ . ‎ 在中，，，‎ 根据勾股定理，在中，‎ ‎，即. ‎ ‎∴ . ‎ 说明：本题中，有两次出现勾股定理，重要的是分清直角三角形，逐步求出欲求线段的长度. ‎ 例05．如图，已知：，，于P. ‎ 求证：. ‎ 分析：图中已有两个直角三角形，但是还没有以BP为边的直角三角形. 因此，我们考虑构造一个以BP为一边的直角三角形. 所以连结BM. 这样，实际上就得到了4个直角三角形. 那么根据勾股定理，可证明这几条线段的平方之间的关系. ‎ 证明：连结BM，‎ 根据勾股定理，在中，‎ ‎. ‎ 而在中，则根据勾股定理有 ‎. ‎ ‎∴‎ 又∵ （已知），‎ ‎∴. ‎ 在中，根据勾股定理有 ‎，‎ ‎ ∴. ‎ 例06．如图，，，，垂足为A，，‎ 求AB的长. ‎ 分析：由于AB是中的一条直角边，故要求AB的长，只要求出BD，AD的长，利用勾股定理即可求出. ‎ 解答：∵，‎ ‎∴，‎ 又∵，垂足为A，‎ ‎∴，‎ ‎∴，‎ ‎∴，‎ ‎∴，‎ 在直角三角形BAD中，，‎ ‎∴，‎ ‎∴‎ 答：AB的长为. ‎ 说明：直角三角形的两直角边的平方和等于斜边的平方，因此只要知道直角三角形的两边长即可求出第三边的长. ‎ 例07．已知：（如图）中，，D为BC上任意一点. ‎ 求证：‎ 分析：在证明线段的平方和、差等问题时，首先考虑的是勾股定理，但这个问题中并没有直接三角形，因为结论中有、，所以考虑到应将AB、AD放在直角三角形中，作为斜边出现较好，于是过A作BC的垂线AE与BC交于E点，再用勾股定理予以证明即可. ‎ 证明：过A作，与BC交于E点 由勾股定理有：‎ 在中，由勾股定理有 ‎∴‎ ‎∵ ‎ ‎∴ ‎ ‎ ∴‎ 例08．已知：（如图）在中，，D、E分别为BC、AC的中点，，. 求AB的长. ‎ 分析：先求BC、AC，再由勾股定理求AB. ‎ 解答：设 ‎∵ AD、BE是中线（已知）‎ ‎∴ ‎ 即 ‎ ‎∵ ‎ ‎∴ ‎ ‎∴‎ 在直角三角形中，‎ ‎∴‎ ‎∴ ‎ 例09．已知：（如图）在中，，，. 求AC的长. ‎ 解答：过A作于E，则 ‎∴ ‎ ‎∴ ‎ 又∵ ‎ ‎∴ ‎ ‎∵ ‎ ‎∴ ‎ 例10．已知：CD为的斜边上的高，且，，，（如图）‎ 求证：‎ 分析：要证这个代数等式，可从左边证到右边. ‎ 证明：左边 ‎∵ 在直角三角形中，‎ 又∵ 即 ‎∴ 右边 即证明出：‎ 例11．如图，中，，，，‎ 求：（1）的周长；（2）的面积. ‎ 分析：从题中条件无法直接求出的周长，可过A点作，构造直角三角形，考虑到本题所给的角度的特殊性，三角形的周长比较容易求出，由于的面积是，从而也不难求出. ‎ 解答：（1）作，垂足为D，‎ 则，为直角三角形，‎ ‎∵ ，‎ ‎，‎ ‎∴ ，，，‎ 在直角三角形BAD中，‎ ‎∵，‎ ‎∵，‎ ‎，‎ 在直角三角形ADC中 ‎∵，‎ ‎∴为等腰直角三角形，‎ ‎∴ ‎ ‎∴的周长 ‎ ‎ ‎ ‎ ‎（2）‎ ‎ ‎ ‎ ‎ ‎ ‎ 答：的周长为，面积为. ‎ 典型例题分析 例1已知：如图，在△ABC中，∠ACB＝，AB＝5cm，BC＝3cm，CD⊥AB于D，‎ 求CD的长.‎ 分析： 本题考查勾股定理的应用，先勾股定理求AC，再运用三角形面积公式得到，于是不难求CD. ‎ 解：∵△ABC是直角三角形，AB＝5，BC＝3，由勾股定理有 A B C D ‎∴∠2＝∠C 又 ‎∴‎ ‎∴CD的长是2.4cm 说明：本题的解题关键是先用勾股定理求AC，再用“面积法”求CD 例2　如图，△ABC中，AB＝AC，∠BAC＝，D是BC上任一点，‎ 求证：‎ 分析：从结论考虑，应将AD放到直角三角形中去，为此考虑过A作垂线段或过D作垂线段，构造Rt△的两种方案，这样就得到两种证法 证法一：过点A作AE⊥BC于E 则在Rt△ADE中，‎ 又∵AB＝AC，∠BAC＝‎ A B C D E ‎∴AE＝BE＝CE 即 证法二：过点D作DE⊥AB于E， DF⊥AC于F 则DE∥AC，DF∥AB A B C D E F 又∵AB＝AC，∠BAC＝‎ ‎∴EB＝ED，FD＝FC＝AE 在Rt△EBD和Rt△FDC中 在Rt△AED中，‎ ‎∴‎ 说明：涉及到三角形中边的平方关系时应考虑运用勾股定理，而勾股定理只有在直角三角形中成立．‎ 例3　设 求证：‎ 分析：本题是一个代数问题，从结构特点即平方关系，考虑运用几何的方法也就是利用勾股定理来解决．‎ b a 证明：构造一个边长的矩形ABCD，如图 E D A 在Rt△ABE中 d c F C B 在Rt△BCF中 在Rt△DEF中 在△BEF中，BE+EF＞BF 即 说明：勾股定理将直角三角形的两边垂直的位置关系转化为数量关系，这为我们运用代数方法研究几何问题提供了工具，反过来，对有些代数问题，我们也可以通过构造直角三角形用勾股定理来解决，即用几何方法解决代数问题．‎ 例4　国家电力总公司为了改善农村用电电费过高的现状，目前正在全国各地农村进行电网改造，某村六组有四个村庄A、B、C、D正好位于一个正方形的四个顶点，现计划在四个村庄联合架设一条线路，他们设计了四种架设方案，如图实线部分．请你帮助计算一下，哪种架设方案最省电线．‎ A B C D A B C D A B C D A B C D O E F 分析：有几种设计方案的，把每种方案的线路长均计算出来，从中择优．‎ 解：不妨设正方形的边长为1，则图1、图2中的总线路长分别为 AD+AB+BC＝3，AB+BC+CD＝3‎ 图3中，在Rt△DGF中 ‎　‎ 同理 ‎∴图3中的路线长为　‎ 图4中，延长EF交BC于H，则FH⊥BC，BH＝CH 由∠FBH＝　及勾股定理得：‎ EA＝ED＝FB＝FC＝‎ ‎∴EF＝1－2FH＝1－‎ ‎∴此图中总线路的长为4EA+EF＝‎ ‎ 3＞2.828>2.732‎ ‎∴图4的连接线路最短，即图4的架设方案最省电线．‎ 说明：在实际生产工作中，往往工程设计的方案比较多，需要运用所学的数学知识进行计算，比较从中选出最优设计．本题利用勾股定理、等腰三角形的判定、全等三角形的性质．‎ 选择题 ‎1．选择题 ‎（1）在中，，D为垂足，则CD等于（ ）‎ ‎（A） （B） （C） （D）‎ ‎（2）正方形的面积是，它的对角线长为（ ）‎ ‎（A） （B） （C） （D）‎ ‎（3）一个长方形的长是宽的2倍，其对角线的长是，那么它的长是（ ）‎ ‎（A） （B） （C） （D）‎ ‎（4）已知等腰三角形的底边，腰，则AC边上的高为（ ）‎ ‎（A） （B） （C） （D）‎ ‎（5）在中，，，AB的垂直平分线交BC于D，，则AC的长是（ ）‎ ‎（A） （B） （C） （D）‎ ‎（6）边长为2的等边三角形内有一点O，那么O到三角形各边的距离之和为（ ）‎ ‎（A）2 （B） （C） （D）‎ ‎（7）等腰三角形腰长为2，底边上的高为1，则它的底边长为（ ）‎ ‎（A） （B） （C） （D） ‎ ‎（8）在中，于D，且，则的面积等于（ ）‎ ‎（A） （B） （C）3 （D）1‎ ‎（9）若是直角三角形，两直角边分别为7和24，在三角形内有一点P到各边的距离相等，则这个距离等于（ ）‎ ‎（A）1 （B）2 （C）3 （D）6‎ 参考答案 ‎1．选择题 ‎（1）A （2）A （3）C （4）C （5）C （6）C （7）A （8）B （9）C 填空题 ‎1．填空题 ‎（1）在中，.‎ ‎①若，则_______. ‎ ‎②若，则________. ‎ ‎③若，则_______. ‎ ‎④若，则________，_______. ‎ ‎⑤若，则_______，_______. ‎ ‎⑥若，则_______，_______. ‎ ‎⑦若，，则________，_______. ‎ ‎（2）在中，，若，_______. ‎ ‎（3）在中，，，则_____，AB边上的高_____. ‎ ‎（4）在中，，，则______. ‎ ‎（5）若直角三角形的一个锐角的外角是，则另一个锐角的外角是________. ‎ ‎（6）在中，，如果，，那么______，______. ‎ ‎（7）等边三角形的任意一条边上的中线长为它的边长的______倍. ‎ ‎（8）在中，，，则______. ‎ 参考答案 ‎1．填空题 ‎（1）①13 ②8 ③ ④6；8 ⑤；4 ⑥； ⑦； ‎ ‎（2）（3）5； （4） （5） ‎ ‎（6） （7） （8）‎ 解答题 ‎1．求作长为的线段. ‎ ‎2．计算题 ‎（1）已知：在中，，且. 的周长为30. 求的各边长和面积. ‎ ‎（2）在中，，，求AC的长. ‎ ‎（3）在中，，于D，，，求CD的长. ‎ ‎（4）已知的面积是，斜边AB的长是，求直角边AC、BC的长. ‎ ‎（5）如图，一铁塔为AB，在离铁塔底部的C处测得，测角仪高为，求铁塔高度. ‎ ‎（6）如图，已知：于M，于B，，，求OM. ‎ ‎ ‎ 参考答案：‎ ‎1．略 ‎2．计算题 ‎（1）设，则由勾股定理可知：，由题意得，∴，∴.‎ ‎（2）解：作于D，则因，∴，∴, ∴‎ ‎（3）解：，∵. 即 ∴. ‎ ‎（4）解：设AC长为，BC为，则有，，可解得或. 因此两直角边长分别为和. ‎ ‎（5）解：，∴，∴‎ ‎（6）解：延长BM交OA于D，则因，∴，∴，∴，又 ∴ ，∴. ‎ 解答题 ‎1．证明题 ‎（1）如图，已知：在中，，D是BC的中点，于E. 求证：. ‎ ‎（2）如图，已知：在中，AD是高，E在BD上，且，且. 求证：. ‎ ‎（3）如图，已知：在中，，P为BC边上一点. ‎ 求证：. ‎ ‎（4）如图，已知：在中，，D为AC上任意一点. ‎ 求证：. ‎ ‎（5）如图，已知：在中，，分别以此直角三角形的三边为直径画半圆. ‎ 参考答案 ‎3．证明题 ‎（1）证明：连结AD，易知，∴，∴‎ ‎（2）证明：. ∴. ∵，∴‎ ‎（3）证明：作于D，则有，‎ 又因，∴‎ ‎（4）证明：，∴. ‎ ‎（5）证明：‎ 阴影部分面积和 ‎，‎ ‎∵，∴，‎ ‎∴阴影部分面积和等于这直角三角形的面积. ‎ 习题精选 A B C M N ‎1、如图，△ABC中，∠ACB=，AC＝12，CB＝5，AM＝AC，BN＝BC，‎ 则MN的长是（　　　　）‎ A、2　 B、2.6 C、3 D、4‎ 答：D ‎2、正方形的面积是，它的对角线长是（　　　　）‎ ‎ A、 B、 C、 D、‎ 答：A ‎3、若一直角三角形二边长为12和5，则第三边长为（　　　）‎ A、13 B、13或 C、13或15 D、15‎ 提示：有两种情况（1）12和5是直角边则第三边为13‎ ‎（2）12为斜边，则第三边为 ‎4、等边三角形的面积为，它的高为（　　　）‎ A、　B、　　C、　　D、‎ 答：C ‎5、在△ABC中，AB＝15，AC＝13，高AD＝12，则△ABC周长为（　　　）‎ A、42　　　B、32　　C、42或32　　D、37或33‎ 答：C A C B D ‎6、如图，在△ABC中，AD⊥BC于D，AB＝AC＝2AD＝m,则△ABC面积是＿＿＿‎ 答：‎ A D B C E F M ‎7、如图，在△ABC中，CE平分∠ACB，CF平分∠ACD，且EF∥BC交AC于M，‎ 若EF＝5，则＝＿＿＿＿‎ 答：25‎ A B C ‎8、如图，△ABC中，AB＝1，AC＝，∠B=45，‎ 求BC的长与△ABC的面积 D 提示：过A点作垂线AD，分别在两个直角三角形 ABD中与ADC中利用勾股定理求解．‎ 答： ‎