中考数学专题复习练习：三角形中我们经常要证明线段相等

中考数学专题复习练习：三角形中我们经常要证明线段相等

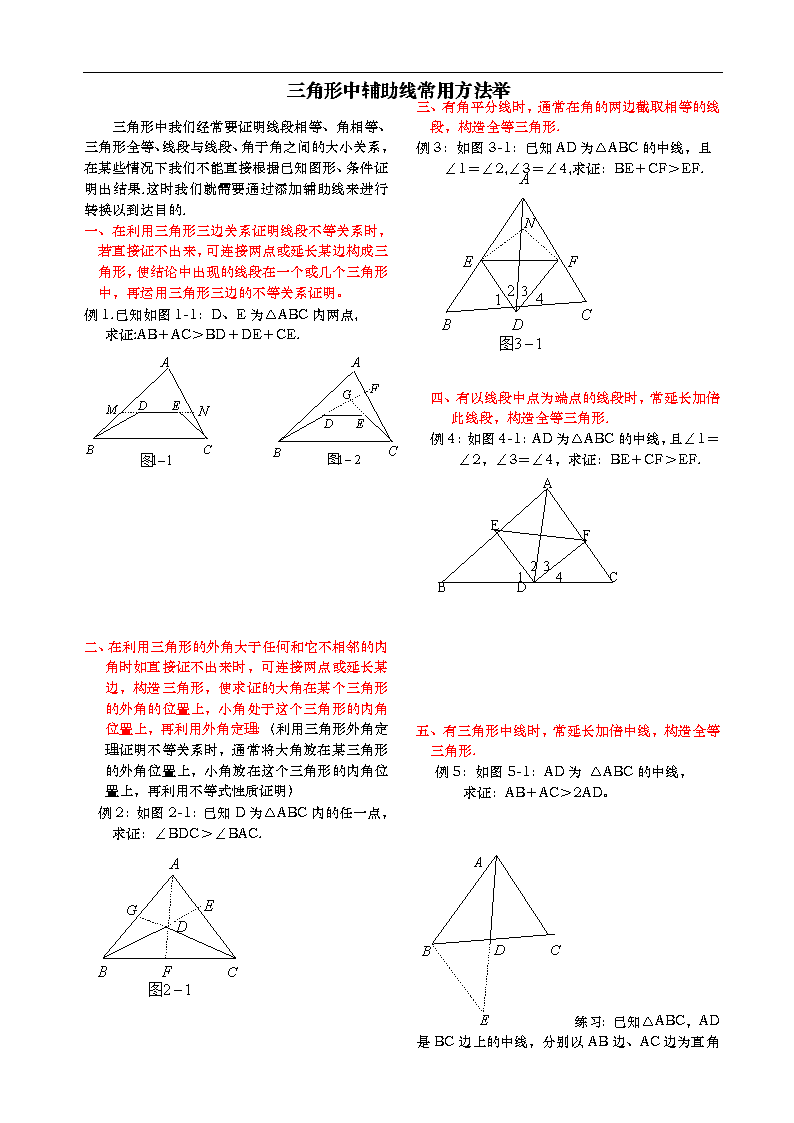
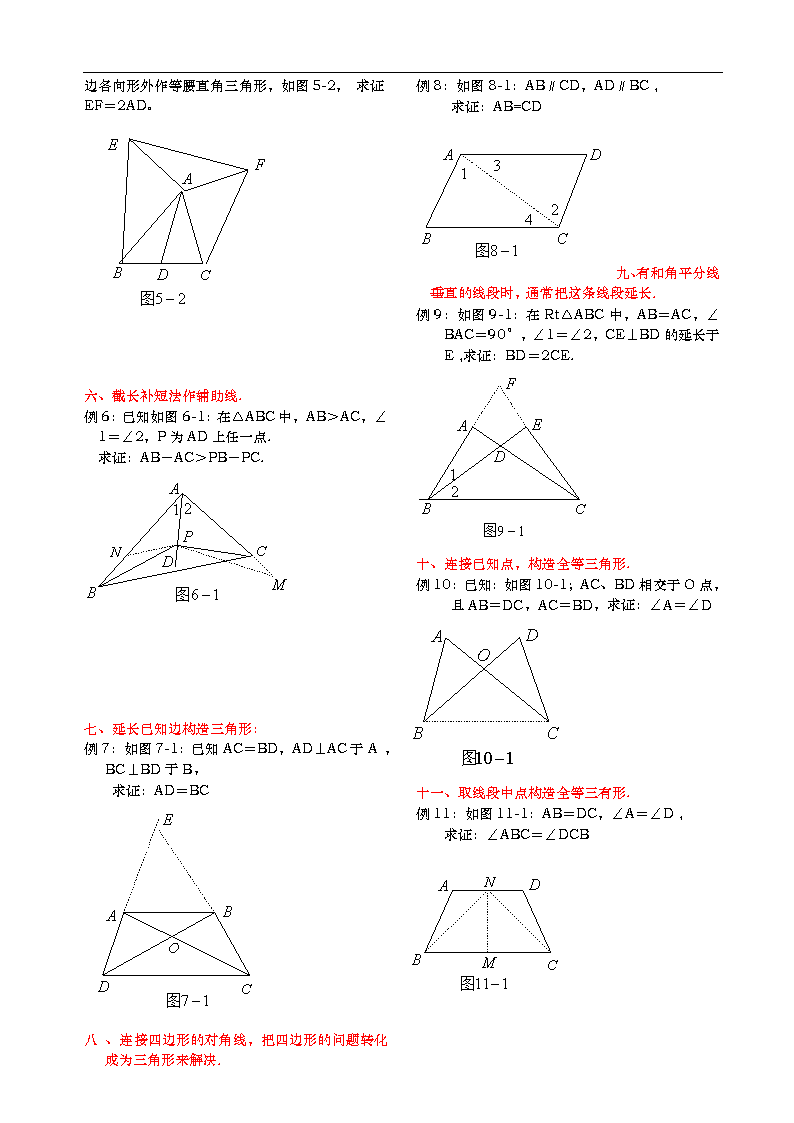
三角形中辅助线常用方法举例 三角形中我们经常要证明线段相等、角相等、三角形全等、线段与线段、角于角之间的大小关系，在某些情况下我们不能直接根据已知图形、条件证明出结果.这时我们就需要通过添加辅助线来进行转换以到达目的.‎ 一、在利用三角形三边关系证明线段不等关系时，若直接证不出来，可连接两点或延长某边构成三角形，使结论中出现的线段在一个或几个三角形中，再运用三角形三边的不等关系证明。‎ 例1.已知如图1-1：D、E为△ABC内两点,‎ 求证:AB＋AC＞BD＋DE＋CE.‎ 二、在利用三角形的外角大于任何和它不相邻的内角时如直接证不出来时，可连接两点或延长某边，构造三角形，使求证的大角在某个三角形的外角的位置上，小角处于这个三角形的内角位置上，再利用外角定理：（利用三角形外角定理证明不等关系时，通常将大角放在某三角形的外角位置上，小角放在这个三角形的内角位置上，再利用不等式性质证明）‎ 例2：如图2-1：已知D为△ABC内的任一点，‎ 求证：∠BDC＞∠BAC.‎ 三、有角平分线时，通常在角的两边截取相等的线 ‎ ‎ 段，构造全等三角形.‎ 例3：如图3-1：已知AD为△ABC的中线，且 ‎∠1＝∠2,∠3＝∠4,求证：BE＋CF＞EF.‎ 四、有以线段中点为端点的线段时，常延长加倍此线段，构造全等三角形.‎ 例4：如图4-1：AD为△ABC的中线，且∠1＝‎ ‎∠2，∠3＝∠4，求证：BE＋CF＞EF.‎ A ‎ B ‎ D ‎ E ‎ F ‎ C ‎ ‎1 ‎ ‎2 ‎ ‎3 ‎ ‎4 ‎ 五、有三角形中线时，常延长加倍中线，构造全等三角形.‎ 例5：如图5-1：AD为 △ABC的中线，‎ 求证：AB＋AC＞2AD。‎ 练习：已知△ABC，AD是BC边上的中线，分 别以AB边、AC边为直角边各向形外作等腰直角三角形，如图5-2， 求证EF＝2AD。 ‎ 六、截长补短法作辅助线.‎ 例6：已知如图6-1：在△ABC中，AB＞AC，∠1＝∠2，P为AD上任一点.‎ 求证：AB－AC＞PB－PC.‎ 七、延长已知边构造三角形：‎ 例7：如图7-1：已知AC＝BD，AD⊥AC于A ，BC⊥BD于B，‎ 求证：AD＝BC 八 、连接四边形的对角线，把四边形的问题转化成为三角形来解决.‎ 例8：如图8-1：AB∥CD，AD∥BC , ‎ 求证：AB=CD 九、有和角平分线垂直的线段时，通常把这条线段延长.‎ 例9：如图9-1：在Rt△ABC中，AB＝AC，∠BAC＝90°，∠1＝∠2，CE⊥BD的延长于E ,求证：BD＝2CE.‎ 十、连接已知点，构造全等三角形.‎ 例10：已知：如图10-1；AC、BD相交于O点，且AB＝DC，AC＝BD，求证：∠A＝∠D 十一、取线段中点构造全等三有形.‎ 例11：如图11-1：AB＝DC，∠A＝∠D ,‎ 求证：∠ABC＝∠DCB