九年级下册数学同步练习28-2-2 第2课时 利用仰俯角解直角三角形 人教版

九年级下册数学同步练习28-2-2 第2课时 利用仰俯角解直角三角形 人教版

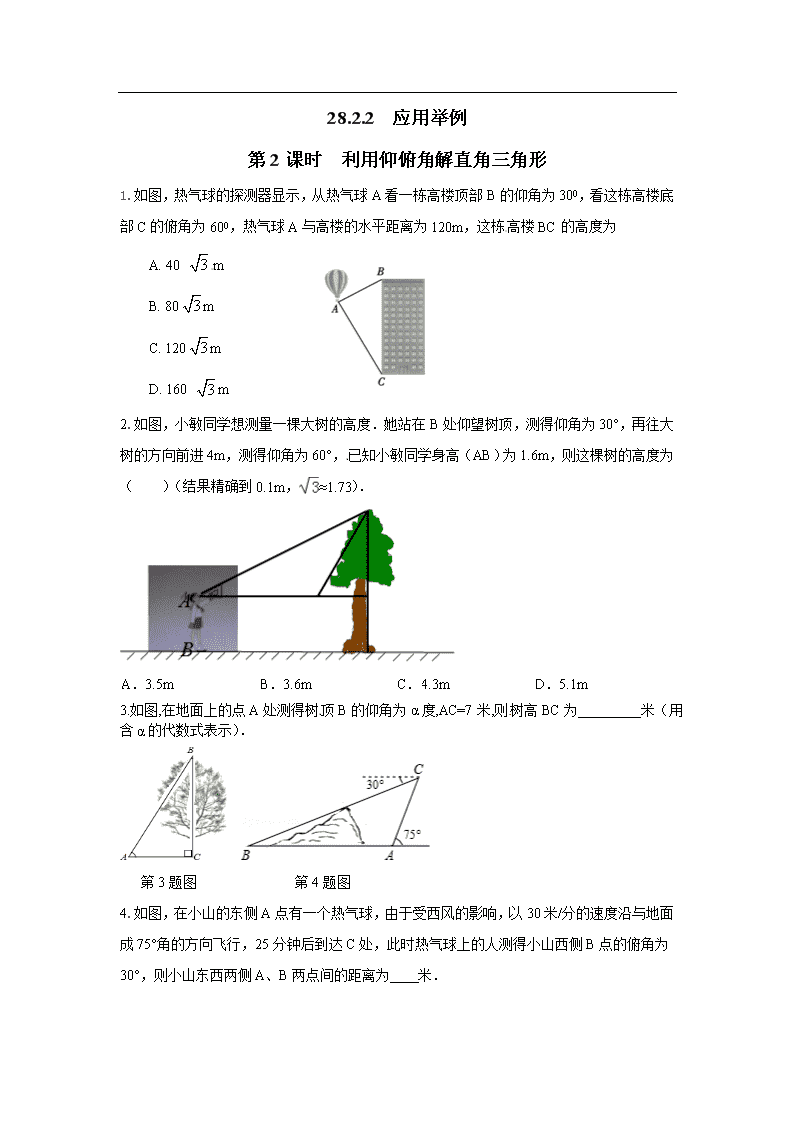
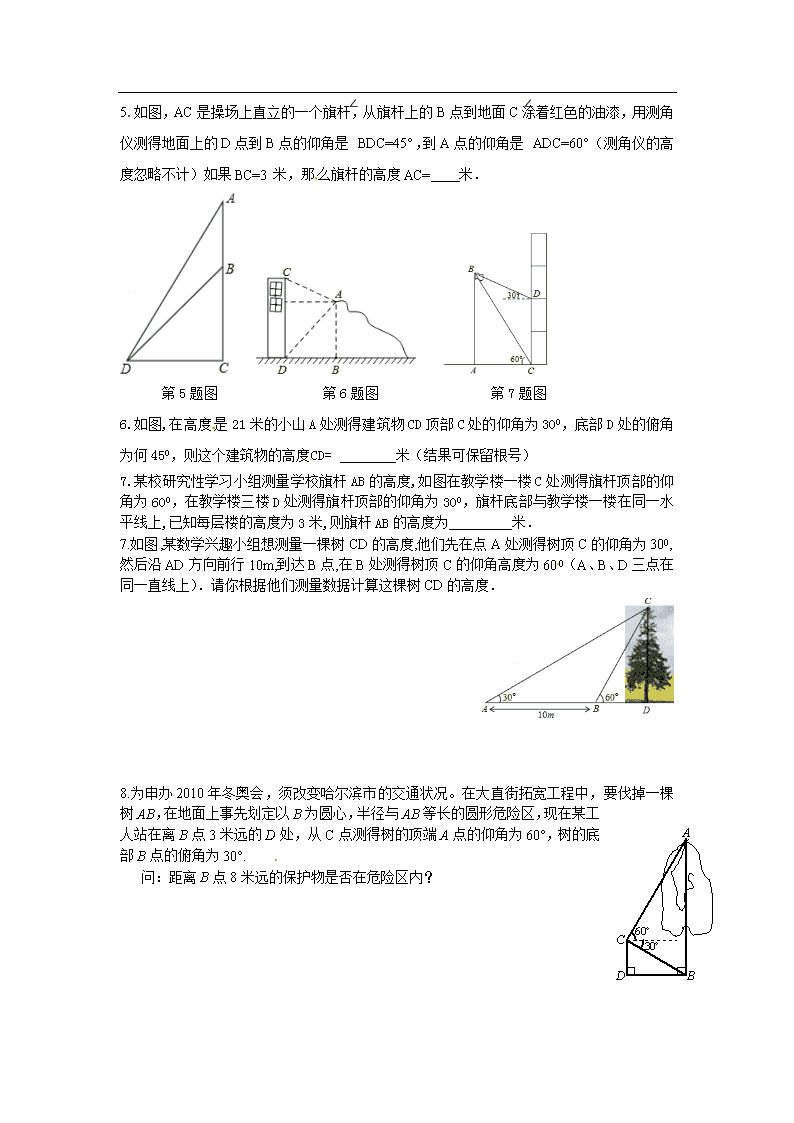
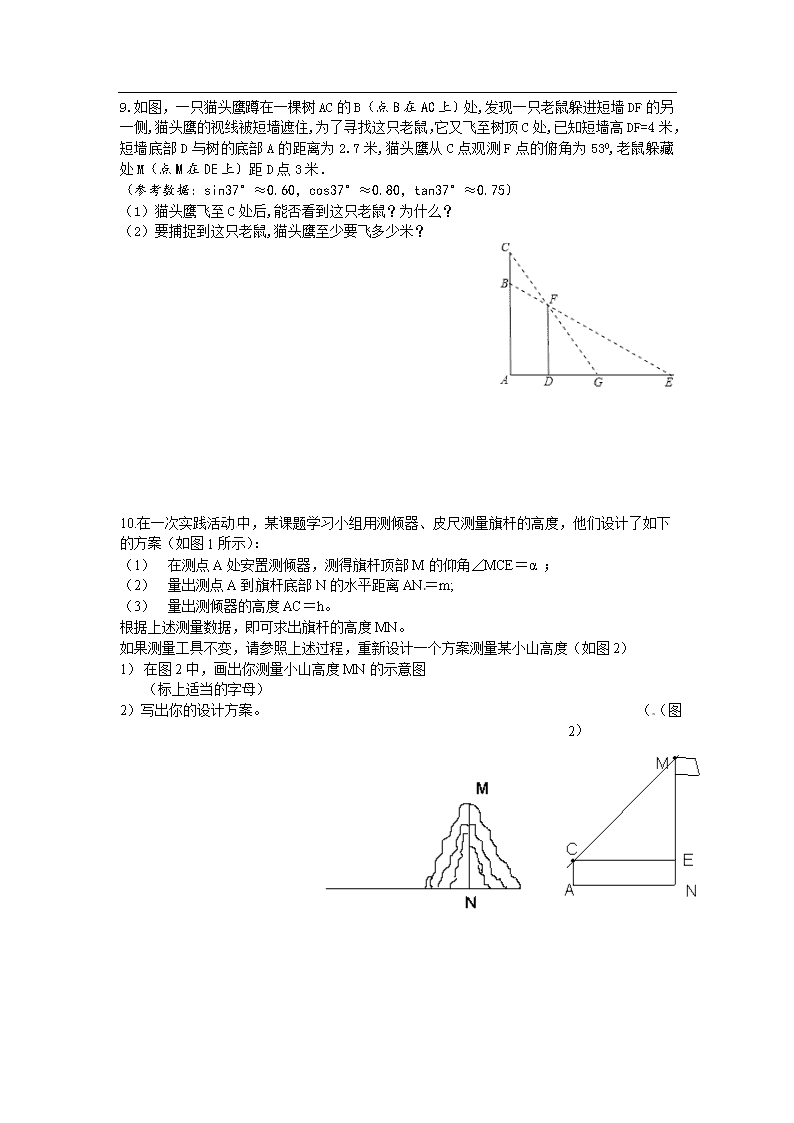
‎28.2.2 应用举例 第2课时 利用仰俯角解直角三角形 ‎1.如图，热气球的探测器显示，从热气球A看一栋高楼顶部B的仰角为300，看这栋高楼底部C的俯角为600，热气球A与高楼的水平距离为120m，这栋高楼BC的高度为 A. 40 m　‎ B. 80m C. 120m 　‎ D. 160 m ‎2.如图，小敏同学想测量一棵大树的高度．她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m，测得仰角为60°，已知小敏同学身高（AB）为1.6m，则这棵树的高度为（　　）（结果精确到0.1m，≈1.73）．‎ ‎　‎ A．‎ ‎3.5m B．‎ ‎3.6m C．‎ ‎4.3m D．‎ ‎5.1m ‎3.如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为　 　米（用含α的代数式表示）．‎ ‎ ‎ ‎ 第3题图 第4题图 ‎4.如图，在小山的东侧A点有一个热气球，由于受西风的影响，以30米/分的速度沿与地面成75°角的方向飞行，25分钟后到达C处，此时热气球上的人测得小山西侧B点的俯角为30°，则小山东西两侧A、B两点间的距离为　　米．‎ ‎5.如图，AC是操场上直立的一个旗杆，从旗杆上的B点到地面C涂着红色的油漆，用测角仪测得地面上的D点到B点的仰角是∠BDC=45°，到A点的仰角是∠ADC=60°（测角仪的高度忽略不计）如果BC=3米，那么旗杆的高度AC=　　米．‎ ‎ ‎ ‎ 第5题图 第6题图 第7题图 ‎6.如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为300，底部D处的俯角为何450，则这个建筑物的高度CD= 米（结果可保留根号）‎ ‎7.某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为600，在教学楼三楼D处测得旗杆顶部的仰角为300，旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为 9‎ 米．‎ ‎7.如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为300,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为600（A、B、D三点在同一直线上）．请你根据他们测量数据计算这棵树CD的高度．‎ ‎8.为申办2010年冬奥会，须改变哈尔滨市的交通状况。在大直街拓宽工程中，要伐掉一棵树AB，在地面上事先划定以B为圆心，半径与AB等长的圆形危险区，现在某工人站在离B点3米远的D处，从C点测得树的顶端A点的仰角为60°，树的底部B点的俯角为30°. [来源:学#科#网Z#X#X#K]‎ ‎ 问：距离B点8米远的保护物是否在危险区内？[来源:学科网]‎ ‎9.如图，一只猫头鹰蹲在一棵树AC的B（点B在AC上）处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠，它又飞至树顶C处,已知短墙高DF=4米，短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为530,老鼠躲藏处M（点M在DE上）距D点3米． （参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75） （1）猫头鹰飞至C处后,能否看到这只老鼠？为什么？ （2）要捕捉到这只老鼠,猫头鹰至少要飞多少米？‎ ‎[来源:学科网ZXXK]‎ ‎10.在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下的方案（如图1所示）：[来源:Z*xx*k.Com]‎ （1） 在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE＝α ；‎ （2） 量出测点A到旗杆底部N的水平距离AN＝m; ‎ （3） 量出测倾器的高度AC＝h。‎ 根据上述测量数据，即可求出旗杆的高度MN。‎ 如果测量工具不变，请参照上述过程，重新设计一个方案测量某小山高度（如图2）‎ 1） 在图2中，画出你测量小山高度MN的示意图 ‎（标上适当的字母）‎ ‎2）写出你的设计方案。 （（图2） ‎ ‎[来源:学#科#网Z#X#X#K]‎