2020九年级数学上册第二章解直角三角形2

2020九年级数学上册第二章解直角三角形2

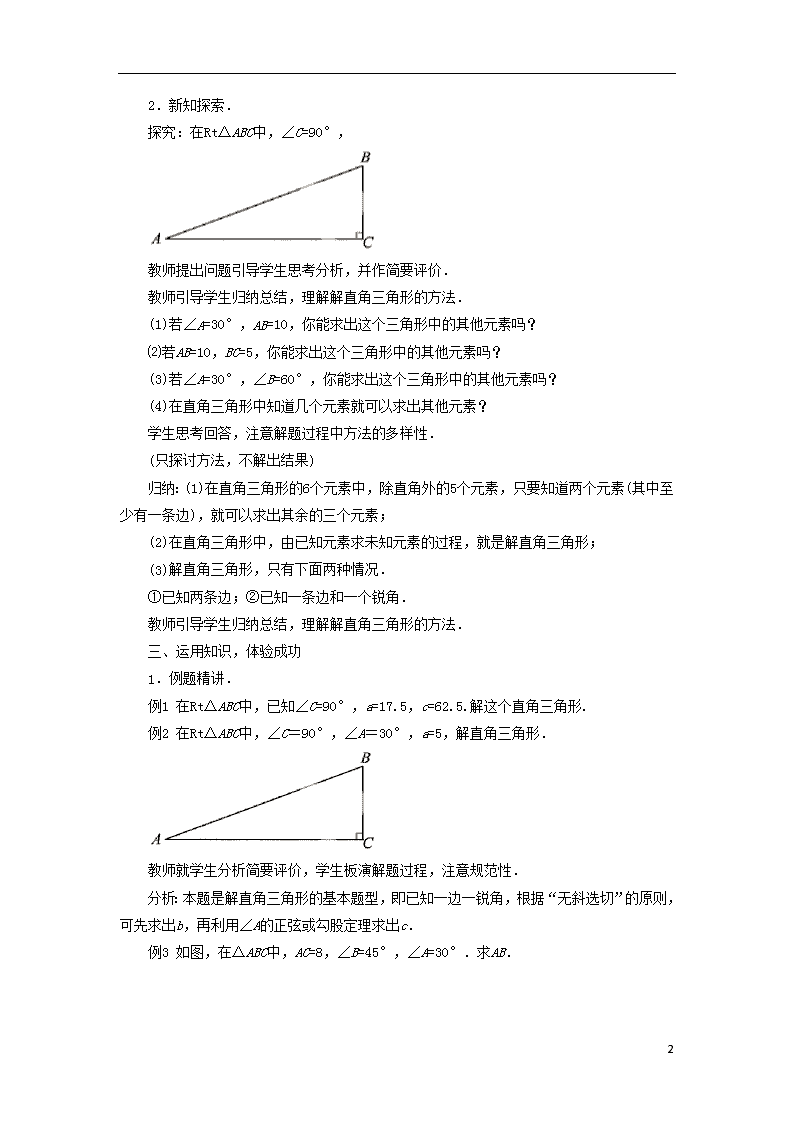
‎《解直角三角形》‎ 教学目标 知识与技能 ‎1．理解直角三角形中5个元素的关系．‎ ‎2．会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形．‎ 数学思考与问题解决 经历解直角三角形的过程，概括出解直角三角形的方法，提高分析问题、解决问题的能力．‎ 情感与态度 在教学活动中，激励学生积极参与，独立思考，能将自己的收获与同伴分享，培养互助合作的团队精神．‎ 重点难点 重点：直角三角形的解法．‎ 难点：正确选用边、角关系求解．‎ 教学设计 一、创设情境，引入新知 出示问题：‎ 在直角三角形中，有3条边、3个角共6个元素，你能根据所学，谈谈它们之间的关系吗？教师提出间题，引起学生思考，然后小组内讨论回答．‎ 二、自主探究，合作交流 ‎1．回顾汇总．‎ 教师根据学生的回答归纳：‎ ‎(1)三边之间的关系：a2+b2=c2(勾股定理)；‎ ‎(2)锐角之间的关系： ∠A+∠B=90°；‎ ‎(3)边角之间的关系：‎ 正弦函数sinA=，‎ 余弦函数cosA=，‎ 正切函数tanA=．‎ 以上三点是解直角三角形的依据，熟知后运用．‎ 教师提出问题，学生思考回答(引问：边与边、角与角、边与角之间的关系)．‎ 学生尝试总结回答，教师讲评汇总．‎ 3‎ ‎2．新知探索．‎ 探究：在Rt△ABC中，∠C=90°，‎ 教师提出问题引导学生思考分析，并作简要评价．‎ 教师引导学生归纳总结，理解解直角三角形的方法．‎ ‎(1)若∠A=30°，AB=10，你能求出这个三角形中的其他元素吗？‎ ‎⑵若AB=10，BC=5，你能求出这个三角形中的其他元素吗？‎ ‎(3)若∠A=30°，∠B=60°，你能求出这个三角形中的其他元素吗？‎ ‎(4)在直角三角形中知道几个元素就可以求出其他元素？‎ 学生思考回答，注意解题过程中方法的多样性．‎ ‎(只探讨方法，不解出结果)‎ 归纳：(1)在直角三角形的6个元素中，除直角外的5个元素，只要知道两个元素(其中至少有一条边)，就可以求出其余的三个元素；‎ ‎(2)在直角三角形中，由已知元素求未知元素的过程，就是解直角三角形；‎ ‎(3)解直角三角形，只有下面两种情况．‎ ‎①已知两条边；②已知一条边和一个锐角．‎ 教师引导学生归纳总结，理解解直角三角形的方法．‎ 三、运用知识，体验成功 ‎1．例题精讲．‎ 例1 在Rt△ABC中，已知∠C=90°，a=17.5，c=62.5.解这个直角三角形.‎ 例2 在Rt△ABC中，∠C＝90°，∠A＝30°，a=5，解直角三角形．‎ 教师就学生分析简要评价，学生板演解题过程，注意规范性．‎ 分析：本题是解直角三角形的基本题型，即已知一边一锐角，根据“无斜选切”的原则，可先求出b，再利用∠A的正弦或勾股定理求出c．‎ 例3 如图，在△ABC中，AC=8，∠B=45°，∠A=30°．求AB．‎ 3‎ 分析：因为△ABC不是直角三角形，因此，我们应设法构造直角三角形来解．‎ 教师分析，引导学生如何将一般三角形转化为直角三角形．‎ 在学生完成的基础上，教师板书解题过程，并归纳如何将斜三角形转化为直角三角形的方法——过三角形的一个顶点作高．‎ 四、总结提髙 ‎1．师生小结．‎ 本节学习了哪些内容？你有哪些认识和收获？‎ 3‎