- 2021-11-11 发布 |
- 37.5 KB |
- 19页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学专题复习练习:相似三角形的判定
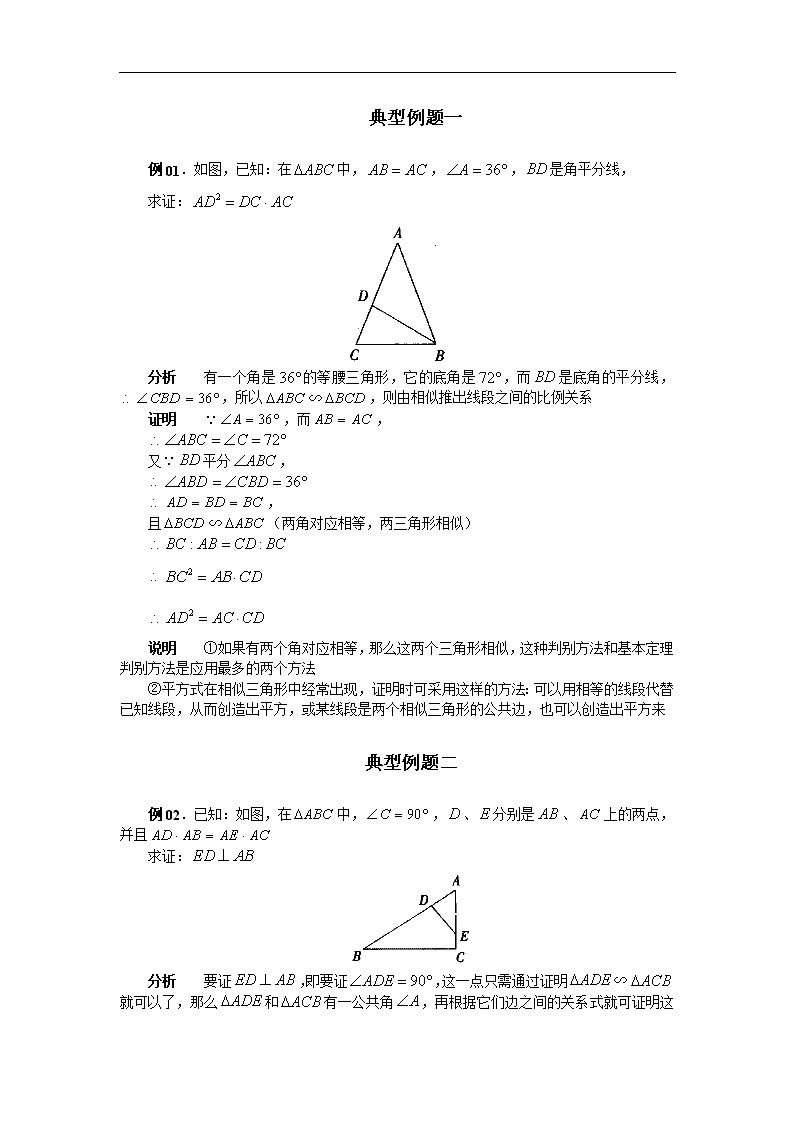
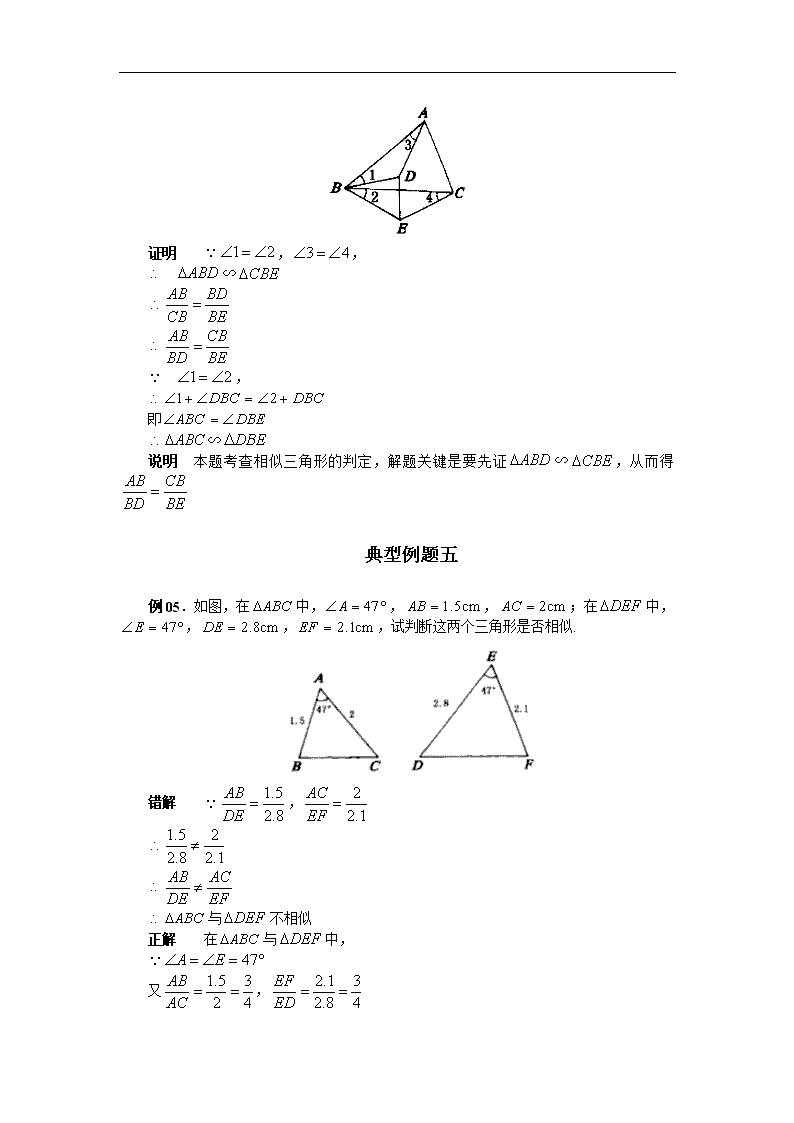
典型例题一 例01.如图,已知:在中,,,是角平分线, 求证: 分析 有一个角是的等腰三角形,它的底角是,而是底角的平分线,,所以∽,则由相似推出线段之间的比例关系 证明 ,而, 又平分, , 且∽(两角对应相等,两三角形相似) 说明 ①如果有两个角对应相等,那么这两个三角形相似,这种判别方法和基本定理判别方法是应用最多的两个方法 ②平方式在相似三角形中经常出现,证明时可采用这样的方法:可以用相等的线段代替已知线段,从而创造出平方,或某线段是两个相似三角形的公共边,也可以创造出平方来 典型例题二 例02.已知:如图,在中,,、分别是、上的两点,并且 求证: 分析 要证,即要证,这一点只需通过证明∽就可以了,那么和有一公共角 ,再根据它们边之间的关系式就可证明这两三角形相似 证明, 又是和的公共角, ∽(两边对应成比例且夹角相等,两三角形相似) 即 说明 如果两个三角形没有互相平行的边,而有公共角时,我们一般使用“两边对应成比例且夹角相等的两个三角形相似”来判定两个三角形相似 典型例题三 例03.如图,已知:在中,,和是的高 求证: 分析 此题是证明线段的倍半关系,采用加倍或折半的方法来证都比较困难,由已知可得和为含有角的直角三角形,因而有, ,所以要证,只须证明∽就可以了. 证明 在中, , 同理,, , ∽(两边对应成比例且夹角相等,两个三角形相似) 说明 证明线段的倍半问题有以下几种方法:(1)取长线段的中点,证其一半等于短线段(折半法);(2)延长短线段为其2倍,证其与较长线段相等(加倍法);(3)用其他线段作媒介,其中经常用的有①三角形两边(或梯形两腰)的中点连线等于底边(或两底之和)的一半;②直角三角形斜边上的中线等于斜边长的一半;③直角三角形中角的对边等于斜边的一半;④利用三角形相似,通过成比例线段证明线段的倍半关系等 典型例题四 例04.如图,已知为内一点,为外一点,且,, 求证:∽ 证明 ,, ∽ , 即 ∽ 说明 本题考查相似三角形的判定,解题关键是要先证∽,从而得 典型例题五 例05.如图,在中,,,;在中,,,,试判断这两个三角形是否相似. 错解 , 与不相似 正解 在与中, 又, ∽ 说明 判定两三角形是否相似,不能依图形的放置方向来考查,而应该按相似三角形的判定方法仔细判定,错解中没有将夹已知角的长边与长边相对应,显然是错误的. 典型例题六 例06.如图,,是是高, 求证: 证明 ,, ∽ , ∽ 说明 本题考查相似三角形判定的应用,解题关键是先证∽,再证∽ 典型例题七 例07.如图,已知:在梯形中,,,,,且 求证: 分析 由已知可得到,要证,可考虑证、所在的两个三角形相似 证明 ,又,,, , 即, 又, ∽(两边对应成比例且夹角相等,两三角形相似) (相似三角形的对应角相等) 说明 利用相似三角形的对应角相等去证明角相等,是证明角相等的又一种方法 典型例题八 例08.如图,已知:是的斜边上的高,为上任意一点,,垂足为 求证: 分析 证明此种类型的题目,常用的方法是先求出平方线段的代换式,由已知是斜边上的高,又,于是,∽,从而,即.要证明此题,还需证明,也就是证明,即.考察这四条线段所在的三角形,可知转为证明∽就行了. 证明 是斜边上的高, ,, ∽(有两个角对应相等,那么这两个三角形相似) , , ∽(有两个角对应相等的两个三角形相似) 典型例题九 例09.如图,已知:在中,,于,在上,若于 求证: 分析 证明,可考虑证∽,由于公用,只需证即可 证明 在中,,, ∽(直角三角形被斜边上的高分成的两个直角和原三角形相似) 同理,在中,,, .又, ∽(两边对应成比例且夹角相等,两三角形相似) 典型例题十 例10.已知:如图,,,,(1)当与,之间满足怎样的关系时,∽;(2)当与,之间满足怎样的关系时, ∽;(3)当与,之间满足怎样的关系时,这两个三角形相似 解答:(1) 当中,∽ 即当时,∽ 故当时,∽ (2), 当时,∽ 即时,∽, 当时,∽ (3)综合(1)(2)可知,当或时这两个三角形相似. 说明 本题是一个条件探索性问题,易错点是弄错对应边或第(3)小题不分类讨论. 典型例题十一 例11.已知:如图,在矩形中,为的中点,交于,连结() (1)与是否相似?若相似,证明你的结论;若不相似,请说明理由 (2)设,是否存在这样的值,使得∽?若存在,证明你的结论并求出值;若不存在,说明理由 分析 这既是一道判断推理性试题,又是一道探索存在性的试题 对于第(1)题,可延长与的延长线交于点 在与中,,, 为的中点 又, , 又与均为直角三角形,∽ 对于第(2)题,如果, 即存在,有∽ 其证明思路是:当时,有 这时,从而可推断, 又均为,∽ 这时值得同学们注意的是:因为不平行于, 不存在第二种相似情况 典型例题十二 例12.如图,在矩形中,厘米,厘米,点沿边从点开始向点以2厘米/秒的速度移动;点沿边向点A以1厘米/秒的速度移动,如果,同时出发,用(秒)表示移动的时间(),那么: (1)当为何值时,为等腰直角三角形? (2)求四边形的面积,提出一个与计算结果有关的结论 (3)当为何值时,以点,,为顶点的三角形与相似? 解答:(1)对于任何时刻,,, 当时,为等腰直角三角形,即,解得(秒) (2)在中, 在中, (厘米) 由计算结果发现:在,两点移动的过程中,四边形的面积始终保持不变. (也可提出:,两点到对角线的距离之和保持不变) (3)根据题意,可分为两种情况来研究. 在矩形中: ①当时,∽,则. 解得(秒) 秒时,∽ ②当时,∽,则. 解得(秒) 当秒时,∽ 说明 本题将“几何一动点”及分类讨论相结合,综合创新命题,全面考查学生素质 三角形相似的判定的典型例题 例1、(上海市,2001)如图1-1,在大小为4×4的正方形方格中,△ABC的顶点A、B、C在单位正方形的顶点上,请在图中画一个 △A1B1C1,使△A1B1C1∽△ABC(相似比不为1),且点A1、B1、C1都在单位正方形的顶点上. 分析:此题是一道开放题,满足条件的图形较多,不能盲目地去画图,关键要抓住图形的特征. 如∠ACB=135°,这样就容易解决. (图1-1) 解:如图1-2,可知∠ABC=∠, 不妨设小正方形的边长为1个单位, 则,, ∴△A1B1C1∽△ABC. ∴ △A1B1C1即为所求. (图1-2) 说明:(1)此题答案有多种,通过本题加强对数学素质和数学能力培养;(2)解此题的关键是认真分析图形,找出切入点,利用所学的知识解决;(3)在判断三角形相似时,要灵活应用定理,如本题要用“两角对应相等,两三角形相似”则较难. 三角形相似的判定的典型例题 例2、如图,平行四边形ABCD中,G是BC延长线上一点,AG与BD交于点E,与DC交于F,则图中相似三角形共有 对 . 分析:图形中相似形较多,不能盲目的取找,先对相似形分类,再计算. 解:由条件可知: (1) △ABD∽△CDB; (2) △ABE∽△DFE; (3) △AED∽△GEB; (4) △ABG∽△FCG∽△FDA,可以组成3对相似三角形. ∴图形中一共有6对相似三角形. 说明:(1) 识图是一种思维训练,它也是能力的培养,在今后的解题中非常重要;(2)△ABG∽△FCG∽△FDA,三个相似的三角形,是怎样组成3对相似三角形?(它是一个组合问题)不妨设这三三角形为a、b、c,则它们可组成:ab、ac;bc.你看出其中的规律了吗?请你考虑4个、5个、……都相似三角形,可以组成多少对相似三角形. 三角形相似的判定的典型例题 例3、(河北省,2001)已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点. 求证:△ADQ∽△QCP. 分析:要找出解决问题的切入点,现已知∠D=∠C=90°,而有很难找出第二个角对应相等,根据条件切入点在边的比,这样问题就解决了. 证明:在正方形ABCD中, ∵Q是CD的中点, ∴. ∵, ∴ 又∵BC=2DQ, ∴, 在△ADQ和△QCP中,,∠C=∠D=90° ∴△ADQ∽△QCP. 说明:解此题的关键是认真分析图形,找出切入点,利用所学的知识解决,灵活应用定理. 选择题 1.如图,于D,于E交AD于F,则图中相似三角形的对数是( ) A.3对 B.4对 C.5对 D. 6对 2.(安徽省,2001)如图,P是的斜边BC上异于B、C的一点,过点P作直线截,使截得的三角形与相似,满足这样条件的直线共有( ) A.1条 B.2条 C.3条 D.4条 3.(威海市,2001)如图,在正方形网络上有6个斜三角形:①,②,③,④,⑤,⑥. 其中,②~⑥中,与三角形①相似的是( ) A.②③④ B.③④⑤ C.④⑤⑥ D.②③⑥ 4.(济南市,2002)下列命题中,真命题是( ) A.对角线相等的四边形是矩形 B.底角相等的两个等腰三角形全等 C.一条对角线将平行四边形分成的两个三角形相似 D.圆是中心对称图形而不是轴对称图形 5.(哈尔滨市,2002)已知:如图,中,P为AB上一点,在下列四个条件中:①;②;③;④ . 其中,能满足和相似的条件是( ) A.①、②、④ B.①、③、④ C.②、③、④ D.①、②、③ 6.如图,F是的AB边上一点,那么下面四个命题中成熟的命题是( ) A.若,则∽ B.若,则∽ C.若,则∽ D.若,则∽ 参考答案; 1.D 2.C 3.B 4.C 5.D 6.D 填空题 1.如图,在中,,交AB于E,,垂足为D,若,,则_______,_______,________. 2.如图,点D在内,连结BD并延长到E,连结AD,AE,若,,则_______度. 3.(宁德市,2002)如图,D,E分别是中AB,AC边上的点,当添加一个条件:_______时,与相似. (注:只需填上你认为正确的一种情况即可) 4.(南京市,2002)下列命题:(1)所有的等腰三角形都相似;(2)所有的等边三角形都相似;(3)所有的等腰直角三角形都相似;(4)所有的直角三角形都相似.其中真命题的序号是_____(注:把所有真命题的序号都填上). 5.(桂林市,2002)如图,正方形ABCD的边上为2,,线段MN的两端在CB,CD上滑动,当______时,与以M,N,C为顶点的三角形相似. 6.(黑龙江省,2000)如图,在中,,过AC上一点D作直线DE,交AB于E,使和相似,这样的直线可作______条. 参考答案: 1.3,, 2. 3. 4. (2)、(3) 5.或 6.两 解答题 1.如图,以DE为轴,折叠等边,顶点A正好落在BC边上F处. 求证:~. 2.如图,梯形ABCD中,,,,,, 求. 3.如图,,, 求证:∽. 4. 在等边中,D在BC上,E在CA上,,AD,BE相交于F. 求证:①∽,②∽. 5.(吉林省,2002)将两块完全相同的等腰直角三角形摆成如图的样子,假设图形中的所有点、线都在同一平面内,回答问题: (1)图中共有多少个三角形?把它们一一写出来; (2)图中有相似(不包括全等)三角形吗?如果有,就把它们一一写出来. 6.已知:如图,AD是的中线,. 求证:. 7.如图,AD是的高,于E,于F. 求证:. 8.如图,中,,D是BC的中点,于F,E是DF的中点. 求证:. 9.如图,中,,M为BC的中点,交CA的延长线于D;交AB于E. 求证:. 10.如图,中,,AD是中线,P是AD上一点,过C作,延长BP交AC于E,交CF于F. 求证:. 11.如图,在中,已知,于D,E为直角边AC的中点,过D,E作直线交AB的延长线于F. 求证:. 12.(河北省,2001)已知:如图,在正方形ABCD中,P是BC上的点,且,Q是CD的中点. 求证:∽. 13.(上海市,2000)如图,在大小为的正方形方格中,的顶点A,B,C在单位正方形的顶点上,请在图中画一个,使∽(相似比不为1),且点,,都在单位正方形的顶点上. 14.(河南省,2000)如图,点C,D在线段AB上,是等边三角形. (1)当AC,CD,DB满足怎样的关系时,∽?(2)当∽时,求的度数. 15. (黄冈市,1999)老师讲完“三角形相似的判定”一节后,出了这样一道思考题:如图,梯形ABCD中,,对角线AC、BD相交于O,问与是否相似,有一位同学解答如下:在与中,∵,∴,又∵,∴∽. 请你判断这位同学的解答是否正确,并说明你判断的理由. 16.(山西省,2001)在方格纸中,每个小格的顶点叫做格点.以格点连线为边的三角形叫做格点三角形.请你在下图的方格纸中,画出两个相似但不全等的格点三角形,并加以证明. (要求:所画三角形是钝角三角形,并标明相应的字母.) 17.(温州市,2001)请设计三种不同的分法,将直角三角形(如图 )分割成四个小三角形,使得每个小三角形与原直角三角形都相似.(画图工具不限,要求画出分割线段,标出能够说明分法的必要记号,不要求证明,不要求写出画法) (注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法) 18.(曲靖市,2001)已知:如图,矩形ABCD,. 在AB上找一点E,使E点与C、D的连线将此矩形分成的三个三角形相似,设. 问:这样的点E是否存在?若存在,这样的点E有几个?请说明理由. 19.如图,在直角梯形ABCD中,,如果,,,那么在AB边上是否存在点P,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似?若不存在,说明理由;若存在,这样的点P有几个?并计算AP的长度. 参考答案: 1.∵,∴,,∴∽ 2.先证∽,可求得,, 3.先证∽ 4.先证,∴. ∴∽. 由得. ∴. ∴∽ 5.(1)共有七个三角形,它们是:、、、、、、. (2)有相似三角形,它们是:∽、∽、∽(或∽∽) 6.,,则∽ 7.证∽,∴. 同理,,则. 证∽ 8.连结AD. 证∽,则, ∴,即. ∵, ∴∽. ∴. ∴,∴ 9.证∽ 10.连结PC,证∽ 11.证∽,∽ 12.证 13.略 14.(1)∵是等边三角形,∴,,从而. ∴当时,∽,即当时,∽;(2)当∽时,. ∴ 15.由于并不表示与的对应边成比例,所以∽成立 16.略 17.略 18.当时,存在一个点E,即AB的中点;当时,不存在;当时,存在两个点E 19.存在,AP的长为或1或6查看更多