七年级上册数学课件《应用一元一次方程—追赶小明》 (5)_北师大版

七年级上册数学课件《应用一元一次方程—追赶小明》 (5)_北师大版

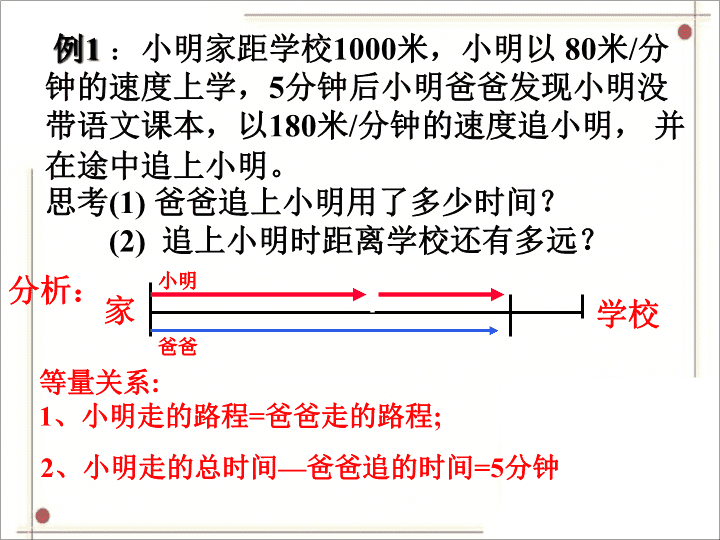
5.6应用一元一次方程 ——追赶小明 基本等量关系为： 路程=速度×时间 速度=路程÷时间 时间=路程÷速度 复习回顾 分析： 等量关系: 1、小明走的路程=爸爸走的路程; 2、小明走的总时间—爸爸追的时间=5分钟 家 学校 爸爸 小明 设经x分钟后爸爸追上小明； 时 间 速 度 路 程 小明 小明爸爸 80 ×(5 +x)米 180x米 80米/分钟 180米/分钟 (5+x)分钟 X分钟 等量关系: 1、小明走的路程=爸爸走的路程; 2、小明走的总时间=爸爸追的时间+5分钟 l 解：（1）设爸爸追上小明用了x分钟， l 据题意得 80×5＋80x=180x. l 解，得 x=4. l 答：爸爸追上小明用了4分钟． l （2）180×4=720（米），1000-720=280（米）. l 答：追上小明时，距离学校还有280米． 解：设快车x小时追上慢车， 据题意得： 85x=450+65x. 解，得 x=22.5. 答：快车22.5小时追上慢车． 练习：甲、乙两站间的路程为450千米，一列慢车从甲站 开出，每小时行驶65千米，一列快车从乙站开出， 每小时行驶85千米．设两车同时开出，同向而行， 则快车几小时后追上慢车？ 分析：等量关系：快车所用时间=慢车所用时间； 快车行驶路程=慢车行驶路程＋相距路程. 问题1：后队追上前队用了多长时间 ？ 议一议:育红学校七年级学生步行到郊外旅行，1班的学生 组成前队，步行的速度为4千米/小时，2班的学生组成后 队，速度为6千米/小时，前队出发１小时后，后队出发， 同时后队派一名联络员骑自行车在两队之间不间断地 来 回进行联络，他骑车的速度为12千米 /小时。 请根据以上的事实提出问题并尝试回答。 问题2：后队追上前队时联络员行了多少路程？ 问题3：联络员第一次追上前队时用了多长时间？ 问题4：当后队追上前队时，他们已经行进了多少路程？ 问题5：联络员在前队出发多少时间后第一次追上前队？ 问题1：后队追上前队用了多长时间 ？ 育红学校七年级学生步行到郊外旅行，1班的学生组成 前队，步行的速度为4千米/小时，2班的学生组成后队， 速度为6千米/小时，前队出发１小时后，后队出发， 同时后队派一名联络员骑自行车在两队之间不间断地 来回进行联络，他骑车的速度为12千米 /小时。 解：设后队追上前队用了x小时，由题 意 列方程得： 6x = 4x + 4 解方程得：x =2 答：后队追上前队时用了2小时。 问题2：后队追上前队时联络员行了多少路程？ 育红学校七年级学生步行到郊外旅行，1班的学生组成 前队，步行的速度为4千米/小时，2班的学生组成后队， 速度为6千米/小时，前队出发１小时后，后队出发， 同时后队派一名联络员骑自行车在两队之间不间断地 来回进行联络，他骑车的速度为12千米 /小时。 解：由问题1得后队追上前队用了2小时，因此 联络员共行进了 12 × 2 = 24 （千米） 答：后队追上前队时联络员行了24千米。 问题3：联络员第一次追上前队时用了多长时间？ 育红学校七年级学生步行到郊外旅行，1班的学生组成 前队，步行的速度为4千米/小时，2班的学生组成后队， 速度为6千米/小时，前队出发１小时后，后队出发， 同时后队派一名联络员骑自行车在两队之间不间断地 来回进行联络，他骑车的速度为12千米 /小时。 解：设联络员第一次追上前队时用了x小时， 由题意列方程得； 12x = 4x + 4 解方程得：x =0.5 答：联络员第一次追上前队时用了0.5小时。 问题4：当后队追上前队时，他们已经行进了多少路程？ 育红学校七年级学生步行到郊外旅行，1班的学生组成 前队，步行的速度为4千米/小时，2班的学生组成后队， 速度为6千米/小时，前队出发１小时后，后队出发， 同时后队派一名联络员骑自行车在两队之间不间断地 来回进行联络，他骑车的速度为12千米 /小时。 解：设当后队追上前队时，他们已经行进了x千米， 由题意列方程得： 1 6 4 x x   解得； x = 12 答：当后队追上前队时，他们已经行进12千米. 问题5：联络员在前队出发多少时间后第一次追上前队？ 育红学校七年级学生步行到郊外旅行，1班的学生组成 前队，步行的速度为4千米/小时，2班的学生组成后队， 速度为6千米/小时，前队出发１小时后，后队出发， 同时后队派一名联络员骑自行车在两队之间不间断地 来回进行联络，他骑车的速度为12千米 /小时。 解：设联络员在前队出发x小时后第一次追上前队， 由题意列方程得； 答：联络员在前队出发后1.5 小时后第一次追上前队. 4x = 12（x - 1） 解方程得： x = 1.5 （1）从时间考虑： 速度慢的用时－速度快的用时＝多用的时间 （2）从路程考虑： 速度快的行程－速度慢的行程＝两者的距离 行程问题中的基本等量关系为： 路程=速度×时间， 一般可从下面两个方面寻找追及问题中 的等量关系： 课堂小结 练习：1、甲乙两人相距40千米，甲在后乙在前，两 人同向而行，甲先出发1.5小时后乙再出发，甲的速 度为每小时8千米，乙的速度为每小时6千米，甲出发 几小时后追上乙？ 解：设甲出发后x小时追上乙，由题意列方程得； 8x – 6（x – 1.5）= 40 答：甲出发后15.5小时追上乙。 甲 乙 40千米 解方程得：x = 15.5 2、甲步行上午7时从A地出发，于下午5时到达B 地，乙骑自行车上午10时从A地出发，于下午3时 到达B地，问乙在什么时间追上甲的？ 分析: 设A，B两地间的距离为1，根据题意得: 甲步行走全程需要10小时，则甲的速度为_______. 乙骑车走全程需要5小时，则乙的速度为_______. 等量关系: 1、甲的用时=乙的用时+3小时 2、甲走的路程=乙走的路程. 10 1 5 1 解（法1）设经y小时后乙追上甲，甲比乙早出发 3小时，由题意列方程得； (y+3) × = y × 解得； y = 3 答：在下午1时乙追上甲。 1 10 1 5 解（法2）设A，B两地间的距离为1，则甲步行 的速度为1/10，乙骑车的速度为1/5， 设在x时乙追上甲，由题意列方程得； （x - 7）× = (x - 10) × 解得； x = 13 答：在下午1时乙追上甲。 1 10 1 5