2015年北京市海淀区高考数学查漏补缺试卷
2015年北京市海淀区高考数学查漏补缺试卷
一、选择题
1. 已知原命题:“若a+b≥2,则a,b 中至少有一个不小于1”,则原命题与其否命题的真假情况是( )
A.原命题为真,否命题为假
B.原命题为假,否命题为真
C.原命题与否命题均为真命题
D.原命题与否命题均为假命题
2. 如图所示,在四边形ABCD中,|CD→|=4,|AD→|=5,AB→⋅AD→=CB→⋅CD→=0,令|BC→|=x,|BA→|=y,则曲线y=f(x)可能是( )
A. B. C. D.
3. 若直线x=3ty=1−4t ,(t为参数)与圆x=3cosθy=b+3sinθ ,(θ为参数)相切,则b=( )
A.−4或6 B.−6或4 C.−1或9 D.−9或1
4. 已知sin(π4−x)=35,则sin2x的值为( )
A.1925 B.1625 C.1425 D.725
5. 设a=sin42∘,b=cos46∘,c=2−12,则( )
A.c
1,b=−2,满足a+b<2.
2.
【答案】
D
【考点】
平面向量数量积的性质及其运算
【解析】
由已知条件便可得到∠BCD=∠BAD=90∘,连接BD后便得到x2+16=y2+25,从而解出y=x2−9,并且得到该函数的定义域为[3, +∞),而符合这一点的只有选项D.
【解答】
根据已知条件知AB⊥AD,CB⊥CD,连接BD,则:
|CB→|2+|CD→|2=|AB→|2+|AD→|2;
∴ x2+16=y2+25;
∴ y=x2−9;
∵ y>0,∴ x>3;
∴ 符合的只有D.
3.
【答案】
A
【考点】
直线与圆的位置关系
参数方程与普通方程的互化
【解析】
先把参数方程化为普通方程,再利用直线与圆相切的充要条件是圆心到直线的距离等于半径,即可求出答案.
【解答】
把直线x=3ty=1−4t ,(t为参数)与圆x=3cosθy=b+3sinθ ,(θ为参数)的参数方程分别化为普通方程得:
直线:4x+3y−3=0,圆:x2+(y−b)2=9,
∵ 此直线与该圆相切,∴ |0+3b−3|42+32=3,解得b=−4,或6.
4.
【答案】
D
【考点】
二倍角的三角函数
【解析】
解法1:利用两角和与差的正弦函数公式及特殊角的三角函数值化简已知的等式,然后将化简后的等式两边平方,利用同角三角函数间的基本关系及二倍角的正弦函数公式化简,即可求出sin2x的值;
解法2:令π4−x=α,求出x,原式变形为sinα的值为35,把x的值代入所求式子中,利用诱导公式化简后,再利用二倍角的余弦函数公式化简,将sinα的值代入即可求出值.
【解答】
法1:由已知得22(cosx−sinx)=35,
两边平方得12(1−sin2x)=925,求得sin2x=725;
法2:令π4−x=α,则sinα=35,
所以sin2x=sin(π2−2α)=cos2α=1−2sin2α=725.
5.
【答案】
C
【考点】
利用不等式比较两数大小
三角函数线
【解析】
将b=cos46∘化为sin44∘,而c=12=22=sin45∘,利用正弦函数(0∘, 45∘)的单调性判断a,b,c的大小.
【解答】
因为b=cos46∘=sin44∘,而c=12=22=sin45∘,
由正弦函数(0∘, 45∘)单调递增,并且42∘<44∘<45∘,
所以sin42∘1时,ax≥x+1恒成立;a=1时,A⊆B成立,
故正实数a的取值范围是[1e,e]
7.
【答案】
D
【考点】
平面的基本性质及推论
空间中平面与平面之间的位置关系
【解析】
此题暂无解析
【解答】
解:若α//β,则由m⊥平面α,n⊥平面β,可得m//n,
这与m,n是异面直线矛盾,故α与β相交.
设α∩β=直线a,过空间内一点P,作m′//m,n′//n,m′与n′相交,m′与n′确定的平面为γ.
因为l⊥m,l⊥n,所以l⊥m′,l⊥n′,所以l⊥γ.
因为m⊥平面α,n⊥平面β,所以m′⊥平面α,n′⊥平面β,
所以a⊥m′,a⊥n′,所以a⊥γ.
因为l⊄ α,l⊄β,所以l与a不重合.
所以l//a.综上知,选D.
故选D.
8.
【答案】
D
【考点】
二项式定理及相关概念
【解析】
求出展开式的通项公式,然后求解即可.
【解答】
(x2−1x)5的展开式的通项公式为:C5rx10−2r(−1x)r=(−1)rC5rx10−3r,
∵ r=0,1,2,3,4,5.
∴ α的值为:10−3r=10,7,4,1,−2,−5.
(x2−1x)5的展开式中含xα(α∈R)的项,则α的值不可能为:2.
9.
【答案】
B
【考点】
函数y=Asin(ωx+φ)的图象变换
【解析】
本题主要考查函数y=Asin(ωx+φ)的图象变换规律,结合正弦函数、余弦函数的图象的对称性可得π3−ϕ=kπ,k∈z,由此求得 ϕ的值.
【解答】
将函数y=sin(2x−ϕ)(0<ϕ<π)的图象沿x轴向左平移π6个单位后得到y=sin[2(x+π6)−ϕ]=sin(2x+π3−ϕ)的图象,
根据所得图象关于原点对称,可得π3−ϕ=kπ,k∈z,∴ ϕ=π3,
二、填空题
【答案】
x=kπ2+π4(k∈Z),(kπ2,−1)(k∈Z)
【考点】
求两角和与差的正弦
【解析】
先利用二倍角公式、和差公式对已知函数进行化简,再结合正弦函数的性质即可求解.
【解答】
解:∵ y=sin2x−2sinxsin(x+π3)+sin3π2,
=sin2x−2sinx(12sinx+32cosx)−1,
=−3sinxcosx−1,
=−32sin2x−1,
令2x=kπ+π2(k∈Z)可得,x=kπ2+π4(k∈Z),
令2x=kπ可得,x=kπ2,
∴ 函数的对称轴为x=kπ2+π4,函数的对称中心为(kπ2,−1)(k∈Z)
故答案为:x=kπ2+π4;(kπ2,−1)(k∈Z)
【答案】
y=x
【考点】
圆的极坐标方程
【解析】
第29页 共32页 ◎ 第30页 共32页
由曲线的极坐标方程可得 ρ2 2sinθcosθ=ρ2,即 (x−y)2=0,从而得 y=x.
【解答】
∵ 曲线的极坐标方程为sin2θ=1,即ρ2 2sinθcosθ=ρ2,∴ 2xy=x2+y2,即 (x−y)2=0,
即 y=x,
【答案】
13,255或−255
【考点】
两角和与差的三角函数
【解析】
直接利用角α的终边与直线y=2x−1垂直,求出终边所在直线的斜率,然后求出cosα,由两角差的正切函数公式即可求tan(α−34π)的值.
【解答】
因为角α的终边与直线y=2x−1垂直,所以终边所在的直线的斜率为:−12,
即tanα=−12,又sin2α+cos2α=1,所以cosα=255或−255,
所以:tan(α−34π)=tanα−tan3π41+tanαtan3π4=(−12)−(−1)1+(−12)×(−1)=13,
【答案】
y
【考点】
直线与椭圆结合的最值问题
【解析】
设A(m, 14m2),F(0, 1),由点A,B关于点F对称得B的坐标,代入准线方程,求得m,进而得到直线AB的方程.
【解答】
抛物线C:x2=4y的焦点为F(0, 1),
设A(m, 14m2),
由题意可得,A,B关于F对称,
可得B(−m, 2−14m2),
代入准线方程y=−1,可得2−14m2=−1,
解得m=±23,
可得AB的斜率为k=±33,
即有直线AB的方程为y=±33x+1.
【答案】
23
【考点】
几何概型计算(与长度、角度、面积、体积有关的几何概型)
【解析】
由题意可得,−1≤a≤1−1≤b≤1为边长为2的正方形,面积为4,由方程bx2+2ax+1=0有两个实根a2≥b,根据积分知识可求其面积,代入概率求解公式可求
【解答】
解:由题意可得,−1≤a≤1−1≤b≤1,其区域为边长为2的正方形,面积为4
∵ 方程bx2+2ax+1=0有两个实根
∴ △=4a2−4b≥0即a2≥b,其区域如图所示的阴影部分
其面积为S=2+−11a2da=13a3 1−1 +2=83
概率P=834=23
故答案为:23
【答案】
1
【考点】
基本不等式及其应用
【解析】
先根据基本不等式得到mn≤14(m+n)2=e2,再根据基本不等式和对数的运算性质即可得到答案.
【解答】
∵ m+n=2e,
∴ mn≤14(m+n)2=e2,
∴ lnm⋅lnn≤14(lnm+lnn)2=14ln2(mn)=1,当且仅当m=n=e时取等号,
∴ lnm⋅lnn的最大值是1,
【答案】
−i32
【考点】
二项式定理的应用
【解析】
第29页 共32页 ◎ 第30页 共32页
利用赋值法,以及二项式定理的简单性质,求解即可.
【解答】
解:(12−ix)10=a0+a1x+a2x2+...+a10x10(i为虚数单位),
令x=12,可得(12−12i)10=a0+12a1+14a2+...+1210a10(i为虚数单位),
而(12−12i)10=[(1−i)2]5210=[−2i]5210=−i32.
故答案为:−i32.
【答案】
π3,27
【考点】
平面向量数量积
【解析】
由已知可得,a→⋅b→−a→2=2,利用向量的数量积的定义代入可求cosθ,进而可求夹角θ
由数量积 性质可知,|2a→−b→|=(2a→−b→)2=4a→2−4a→⋅b→+b→2,代入可求
【解答】
解:∵ |a→|=1,|b→|=6,a→⋅(b→−a→)=2
∴ a→⋅b→−a→2=2
∴ 1×6cosθ−1=2
∴ cosθ=12
∵ 0≤θ≤π
∴ θ=13π
∵ |2a→−b→|=(2a→−b→)2=4a→2−4a→⋅b→+b→2=4−4×1×6×12+36=27
故答案为:13π,27
【答案】
72
【考点】
分层抽样方法
古典概型及其概率计算公式
【解析】
按分层抽样应该从老年职工组中抽取18×19=2人,设老年职工组共有n人,由老年职工组中的甲、乙二人均被抽到的概率是128,能求出该单位员工总数.
【解答】
按分层抽样应该从老年职工组中抽取18×19=2人,
设老年职工组共有n人,
则甲乙二人均被抽到的概率为:C22Cn2=128,
解得:n=8,所以该单位共有员工8×9=72人.
【答案】
2
【考点】
多面体和旋转体表面上的最短距离问题
【解析】
建立如图所示空间直角坐标系,设出E点坐标,利用B1到平面A1EC的距离为216求得a的值得答案.
【解答】
建立如图所示的空间直角坐标系,
设E(a, 0, 0),C(1, 1, 0),A1(0, 0, 1),B1(1, 0, 1).
则A1C→=(1,1,−1),A1E→=(a,0,−1),
设平面A1EC的一个法向量为n→=(x,y,z),
由n→⋅A1C→=0n→⋅A1E→=0 ,得x+y−z=0ax−z=0 ,取z=a,则x=1,y=a−1.
∴ n→=(1,a−1,a).
A1B1→=(1,0,0),
由|A1B1→⋅n→||n→|=11+a2+(a−1)2=216,解得:a=7±2114.
∴ E所有可能的位置有2个.
【答案】
,4
【考点】
由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】
化简可得h=2sin(t+π4),由初相和振幅的意义可得答案.
第29页 共32页 ◎ 第30页 共32页
【解答】
化简可得h=2sint+2cost
=2(22sint+22cost)
=2sin(t+π4),
令t=0可得h=2,
由振幅为2可得小球振动时最大的高度差为4
【答案】
2e
【考点】
利用导数研究曲线上某点切线方程
【解析】
设f(x)=x2与g(x)=alnx,再设公共点(x0, y0),根据题意得到,f(x0)=g(x0),f′(x0)=g′(x0),解出a即得.
【解答】
设f(x)=x2与g(x)=alnx在公共点(x0, y0)处的切线相同.
f′(x)=2x,g′(x)=ax.
由题意知f(x0)=g(x0),f′(x0)=g′(x0)
即 2x0=ax0x02=alnx0 ,
解得a=2e.
【答案】
−2
【考点】
双曲线的离心率
【解析】
化双曲线的方程为标准形式,可得渐近线的方程,结合已知可得关于k的方程,解之可得.
【解答】
双曲线2x2+ky2=k的方程可化为y2−x2−k2=1,
可得a=1,b=−k2,
故渐近线y=±−2kx,
由题意可得−2k=1,解得k=−2.
【答案】
2,π3
【考点】
由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】
根据题意可得 T2<2π30;
当x∈(2kπ+π4,2kπ+5π4),k∈Z时,f′(x)<0,
所以f(x)的单调递增区间是(2kπ−3π4,2kπ+π4),k∈Z,
单调递减区间是(2kπ+π4,2kπ+5π4),k∈Z.
(2)由(Ⅰ)知,f(x)在[−π,−3π4)上单调递减,在(−3π4,π4)上单调递增,在(π4,π]上单调递减,
而f(−π)=0,f(π4)=22e−π4>0,f(π)=0,f(−3π4)=−22e3π4<0
所以f(x)在[−π, π]上的最大值为22e−π4,最小值为−22e3π4.
【考点】
利用导数研究函数的单调性
利用导数研究函数的最值
【解析】
(Ⅰ)先求出函数的导数,令f′(x)=0,从而求出函数的单调区间;(Ⅱ)先求出函数在[−π, π]上的单调区间,从而求出函数的最值.
【解答】
(1)f′(x)=−e−xsinx+e−xcosx=2cos(x+π4)ex.
令f′(x)=0,解得:x=kπ+π4,k∈Z.
因为当x∈(2kπ−3π4,2kπ+π4),k∈Z时,f′(x)>0;
当x∈(2kπ+π4,2kπ+5π4),k∈Z时,f′(x)<0,
所以f(x)的单调递增区间是(2kπ−3π4,2kπ+π4),k∈Z,
单调递减区间是(2kπ+π4,2kπ+5π4),k∈Z.
(2)由(Ⅰ)知,f(x)在[−π,−3π4)上单调递减,在(−3π4,π4)上单调递增,在(π4,π]上单调递减,
而f(−π)=0,f(π4)=22e−π4>0,f(π)=0,f(−3π4)=−22e3π4<0
所以f(x)在[−π, π]上的最大值为22e−π4,最小值为−22e3π4.
【答案】
(1)由f(x)=exx2+2x+b的定义域是R,知4−4b<0得b>1.f′(x)=ex(x2+2x+b−2x−2)(x2+2x+b)2=ex(x2+b−2)(x2+2x+b)2,
由f′(x)=0得x2=2−b≥0,故b≤2.
当b=2时,f′(x)=x2ex(x2+2x+2)2≥0,函数f(x)在R上单调递增,无极值点.
∴ 所求范围为112)
记g(x)=ex−(x+1)(0≤x<1),g′(x)=ex−1≥0
∴ g(x)在[0, 1)上是单调递增函数
∴ 当x∈(0, 1)时,g(x)>g(0)=0,即ex>x+1
由n=2−b∈(0,1)知,en2n+2>n+12n+2=12.
这说明f(x)=12在(m, +∞)上无解.
又f(−2)=e−2b<1e2<12,f(m)>f(n)>12,且f(x)在(−∞, m)上单调递增,
∴ f(x)=12在(−∞, m)上恰有一解
综上所述,f(x)=12在R上恰有一解.
【考点】
函数的零点
函数在某点取得极值的条件
【解析】
(Ⅰ)求导数,定义域是R,知4−4b<0得b>1;由f′(x)=0得x2=2−b≥0,故b≤2.当b=2时,f′(x)=x2ex(x2+2x+2)2≥0,函数f(x)在R上单调递增,无极值点,即可求实数b的取值范围;
(Ⅱ)由(Ⅰ)知函数f(x)的两个极值点为m=−2−b∈(−1,0),n=2−b∈(0,1),说明f(x)=12在(m, +∞)上无解,f(x)=12在(−∞, m)上恰有一解.
【解答】
(1)由f(x)=exx2+2x+b的定义域是R,知4−4b<0得b>1.f′(x)=ex(x2+2x+b−2x−2)(x2+2x+b)2=ex(x2+b−2)(x2+2x+b)2,
由f′(x)=0得x2=2−b≥0,故b≤2.
当b=2时,f′(x)=x2ex(x2+2x+2)2≥0,函数f(x)在R上单调递增,无极值点.
∴ 所求范围为112)
记g(x)=ex−(x+1)(0≤x<1),g′(x)=ex−1≥0
∴ g(x)在[0, 1)上是单调递增函数
∴ 当x∈(0, 1)时,g(x)>g(0)=0,即ex>x+1
由n=2−b∈(0,1)知,en2n+2>n+12n+2=12.
这说明f(x)=12在(m, +∞)上无解.
又f(−2)=e−2b<1e2<12,f(m)>f(n)>12,且f(x)在(−∞, m)上单调递增,
∴ f(x)=12在(−∞, m)上恰有一解
综上所述,f(x)=12在R上恰有一解.
【答案】
第29页 共32页 ◎ 第30页 共32页
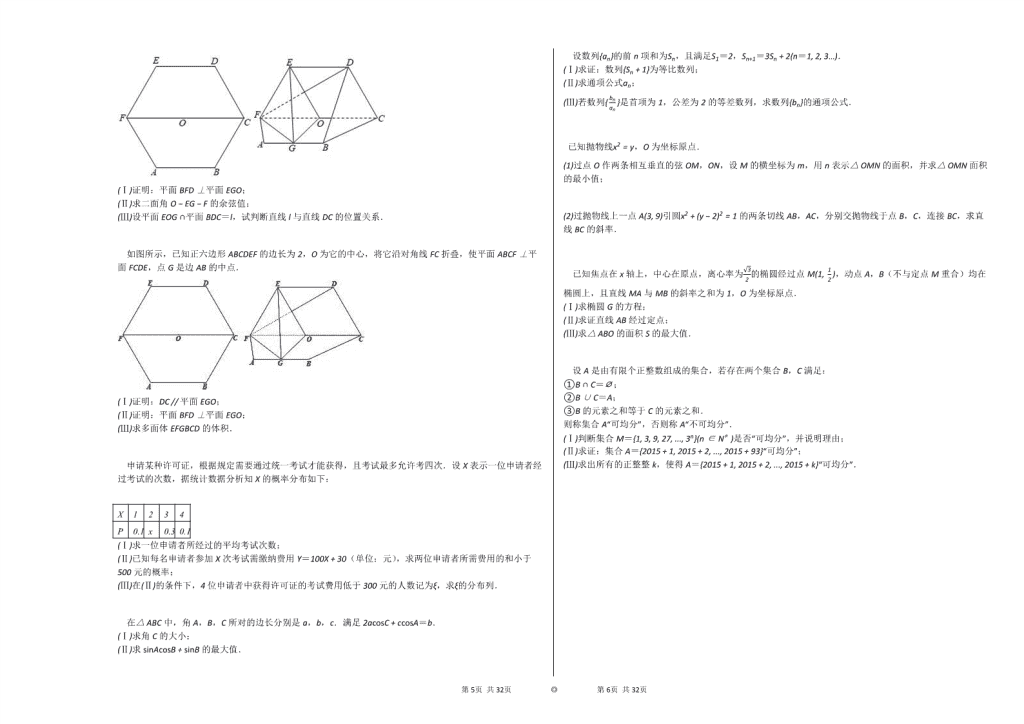
(1)证明:∵ O是正六边形ABCDEF的中心,G是边AB的中点;
∴ OE⊥FD,OG⊥FC;
∵ 平面ABCF⊥平面FCDE,平面ABCF∩平面FCDE=FC,GO⊂平面ABCF;
∴ GO⊥平面FCDE,DF⊂平面FCDE;
∴ GO⊥DF;
又EO∩GO=O;
∴ DF⊥平面EGO,DF⊂平面BFD;
∴ 平面BFD⊥平面EGO;
(2)取DE的中点H,连接OH,则OH⊥FC,由上面知OG⊥平面FCDE;
∴ OG,OC,OH三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示的空间直角坐标系,则:
G(3,0,0),D(0,1,3),E(0,−1,3),F(0, −2, 0);
∴ FD→=(0,3,3),FE→=(0,1,3),FG→=(3,2,0);
由(Ⅰ)知:DF⊥平面EGO.
所以平面EGO的一个法向量为FD→=(0,3,3);
设平面EFG的法向量为m→=(x,y,z),则m→⋅FE→=0m→⋅FG→=0 ,即y+3z=03x+2y=0. ;
令y=3,则z=−1,x=−2,∴ m→=(−2,3,−1);
∴ 二面角O−EG−F的余弦值为cos=(−2,3,−1)⋅(0,3,3)4+3+1⋅0+9+3=24;
(Ⅲ)证明:在正六边形ABCDEF中,OC // ED,OC=ED;
∴ 四边形OCDE是平行四边形;
∴ DC // EO;
∵ OE⊂平面OEG,CD⊄平面OEG;
∴ CD // 平面OEG;
因为平面EOG∩平面BDC=l,CD⊂平面BDC;
所以DC // l.
【考点】
二面角的平面角及求法
空间中直线与直线之间的位置关系
平面与平面垂直
【解析】
(Ⅰ)根据已知条件能够得到DF⊥OE,OG⊥CF,而平面ABCF⊥平面FCDE,从而得到OG⊥平面FCDE,从而得到DF⊥OG,从而得到DF⊥平面EGO,由面面垂直的判定定理即可得出平面BFD⊥平面EGO;
(Ⅱ)取DE中点H,并连接OH,从而可分别以边OG,OC,OH所在直线为x,y,z轴,建立空间直角坐标系,求出一些点的坐标.由(Ⅰ)可知FD→=(0,3,3)为平面EGO的一个法向量,可设平面EFG的法向量为m→=(x,y,z),而根据m→⋅FE→=0m→⋅FG→=0 即可求出m→,从而由cos即可求得二面角O−EG−F的余弦值;
(Ⅲ)容易说明DC // EO,从而得到DC // 平面EOG,而平面EOG∩平面BDC=l,从而由线面平行的性质定理即可得出DC // l.
【解答】
(1)证明:∵ O是正六边形ABCDEF的中心,G是边AB的中点;
∴ OE⊥FD,OG⊥FC;
∵ 平面ABCF⊥平面FCDE,平面ABCF∩平面FCDE=FC,GO⊂平面ABCF;
∴ GO⊥平面FCDE,DF⊂平面FCDE;
∴ GO⊥DF;
又EO∩GO=O;
∴ DF⊥平面EGO,DF⊂平面BFD;
∴ 平面BFD⊥平面EGO;
(2)取DE的中点H,连接OH,则OH⊥FC,由上面知OG⊥平面FCDE;
∴ OG,OC,OH三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示的空间直角坐标系,则:
G(3,0,0),D(0,1,3),E(0,−1,3),F(0, −2, 0);
∴ FD→=(0,3,3),FE→=(0,1,3),FG→=(3,2,0);
由(Ⅰ)知:DF⊥平面EGO.
所以平面EGO的一个法向量为FD→=(0,3,3);
设平面EFG的法向量为m→=(x,y,z),则m→⋅FE→=0m→⋅FG→=0 ,即y+3z=03x+2y=0. ;
令y=3,则z=−1,x=−2,∴ m→=(−2,3,−1);
∴ 二面角O−EG−F的余弦值为cos=(−2,3,−1)⋅(0,3,3)4+3+1⋅0+9+3=24;
(Ⅲ)证明:在正六边形ABCDEF中,OC // ED,OC=ED;
∴ 四边形OCDE是平行四边形;
∴ DC // EO;
∵ OE⊂平面OEG,CD⊄平面OEG;
∴ CD // 平面OEG;
因为平面EOG∩平面BDC=l,CD⊂平面BDC;
所以DC // l.
【答案】
第29页 共32页 ◎ 第30页 共32页
(1)证明:在正六边形ABCDEF中,OC // ED,OC=ED,
∴ 四边形OCDE是平行四边形.
∴ DC // EO.
∵ OE⊂平面OEG,CD⊄平面OEG,
∴ CD // 平面OEG;
(2)证明:∵ O是正六边形ABCDEF的中心,G是边AB的中点,
∴ OE⊥FD,OG⊥AB.
∵ 平面ABCF⊥平面FCDE,平面ABCF∩平面FCDE=FC,GO⊂平面ABCF,
∴ GO⊥平面FCDE.
∵ DF⊂平面FCDE,
∴ GO⊥DF.
∵ EO⊂平面EOG,GO⊂平面EOG,EO∩GO=O,
∴ DF⊥平面EGO.
∵ DF⊂平面DFB,
∴ 平面BFD⊥平面EGO;
(Ⅲ)由(Ⅱ)知GO⊥平面FCDE.
∴ VEFGBCD=VB−CDEF+VB−FEG
=VB−CDEF+12VG−FEO
=13S△CDEF⋅GO+16S△FEO⋅GO
=13×12(2+4)×3×3+16×12×2×3×3=72.
【考点】
直线与平面平行
平面与平面垂直
【解析】
(Ⅰ)由圆平面图形得到OC // ED,OC=ED,从而证得四边形OCDE是平行四边形,得到DC // EO,然后由线面平行的判定定理得答案;
(Ⅱ)由正六边形的性质及G是边AB的中点,得到OE⊥FD,再由面面垂直的判定及性质得到OG⊥DF.由线面垂直的判定得DF⊥平面EGO,再由面面垂直的判定得答案;
(Ⅲ)把多面体EFGBCD的体积色体积转化为VB−CDEF+VB−FEG,求出两个棱锥的体积得答案.
【解答】
(1)证明:在正六边形ABCDEF中,OC // ED,OC=ED,
∴ 四边形OCDE是平行四边形.
∴ DC // EO.
∵ OE⊂平面OEG,CD⊄平面OEG,
∴ CD // 平面OEG;
(2)证明:∵ O是正六边形ABCDEF的中心,G是边AB的中点,
∴ OE⊥FD,OG⊥AB.
∵ 平面ABCF⊥平面FCDE,平面ABCF∩平面FCDE=FC,GO⊂平面ABCF,
∴ GO⊥平面FCDE.
∵ DF⊂平面FCDE,
∴ GO⊥DF.
∵ EO⊂平面EOG,GO⊂平面EOG,EO∩GO=O,
∴ DF⊥平面EGO.
∵ DF⊂平面DFB,
∴ 平面BFD⊥平面EGO;
(Ⅲ)由(Ⅱ)知GO⊥平面FCDE.
∴ VEFGBCD=VB−CDEF+VB−FEG
=VB−CDEF+12VG−FEO
=13S△CDEF⋅GO+16S△FEO⋅GO
=13×12(2+4)×3×3+16×12×2×3×3=72.
【答案】
(1)由X的概率分布列可得0.1+x+0.1+0.3=1,∴ x=0.5.
∴ E(X)=0.1×1+0.5×2+0.3×3+0.1×4=2.4.
所以一位申请者所经过的平均考试次数为2.4次.
(2)设两位申请者均经过一次考试为事件A,有一位申请者经历两次考试一位申请者经历一次考试为事件B,两位申请者经历两次考试为事件C,有一位申请者经历三次考试一位申请者经历一次考试为事件D.
因为考试需交费用Y=100X+30,两位申请者所需费用的和小于500元的事件为A∪B∪C∪D.
∴ P(A∪B∪C∪D)=0.1×0.1+2×0.5×0.5+0.3×0.3+2×0.1×0.3=0.66
所以两位申请者所需费用的和小于500元的概率为0.66.
(Ⅲ)一位申请者获得许可证的考试费用低于300元的概率为35,ξ的可能取值为0,1,2,3,4.
P(ξ=0)=(25)4=16625,P(ξ=1)=C41(35)(25)3=96625,P(ξ=2)=C42(35)2(25)2=216625,
P(ξ=3C43(35)3(25)=216625, P(ξ=4)=(35)4=81625.
ξ的分布列为
ξ
0
1
2
3
4
P
16625
96625
216625
216625
81625
【考点】
离散型随机变量及其分布列
【解析】
(Ⅰ)由X的概率分布列的性质,先求x的值,再计算其期望,即可求得一位申请者所经过的平均考试次数;
(Ⅱ)设两位申请者均经过一次考试为事件A,有一位申请者经历两次考试一位申请者经历一次考试为事件B,两位申请者经历两次考试为事件C,有一位申请者经历三次考试一位申请者经历一次考试为事件D,因为考试需交费用Y=100X+30,两位申请者所需费用的和小于500元的事件为A∪B∪C∪D,由此可求两位申请者所需费用的和小于500元的概率;
(Ⅲ)一位申请者获得许可证的考试费用低于300元的概率为35,ξ的可能取值为0,1,2,3,4,求出相应的概率,即可得到的分布列.
【解答】
(1)由X的概率分布列可得0.1+x+0.1+0.3=1,∴ x=0.5.
∴ E(X)=0.1×1+0.5×2+0.3×3+0.1×4=2.4.
所以一位申请者所经过的平均考试次数为2.4次.
(2)设两位申请者均经过一次考试为事件A,有一位申请者经历两次考试一位申请者经历一次考试为事件B,两位申请者经历两次考试为事件C,有一位申请者经历三次考试一位申请者经历一次考试为事件D.
因为考试需交费用Y=100X+30
第29页 共32页 ◎ 第30页 共32页
,两位申请者所需费用的和小于500元的事件为A∪B∪C∪D.
∴ P(A∪B∪C∪D)=0.1×0.1+2×0.5×0.5+0.3×0.3+2×0.1×0.3=0.66
所以两位申请者所需费用的和小于500元的概率为0.66.
(Ⅲ)一位申请者获得许可证的考试费用低于300元的概率为35,ξ的可能取值为0,1,2,3,4.
P(ξ=0)=(25)4=16625,P(ξ=1)=C41(35)(25)3=96625,P(ξ=2)=C42(35)2(25)2=216625,
P(ξ=3C43(35)3(25)=216625, P(ξ=4)=(35)4=81625.
ξ的分布列为
ξ
0
1
2
3
4
P
16625
96625
216625
216625
81625
【答案】
(1)由正弦定理及2acosC+ccosA=b.
得2sinAcosC+sinCcosA=sinB
在△ABC中,A+B+C=π,
∴ A+C=π−B,即sin(A+C)=sinB.
∴ 2sinAcosC+sinCcosA=sin(A+C)+sinAcosC=sinB+sinAcosC=sinB
∴ sinAcosC=0
又∵ 00.
∴ cosC=0
∴ C=12π
(2)由(Ⅰ)得C=12π,
∴ A+B=12π,即B=12π−A.
∵ sinAcosB+sinB=cos2B+sinB=−sin2B+sinB+1=−(sinB−12)2+54
∵ 00.
∴ cosC=0
∴ C=12π
(2)由(Ⅰ)得C=12π,
∴ A+B=12π,即B=12π−A.
∵ sinAcosB+sinB=cos2B+sinB=−sin2B+sinB+1=−(sinB−12)2+54
∵ 01时,an=Sn−Sn−1=(3n−1)−(3n−1−1)
=3n−1(3−1)=2×3n−1.
故an=2×3n−1,n∈N*;
(Ⅲ)∵ 数列{bnan}是首项为1,公差为2的等差数列,
∴ bnan=1+2(n−1)=2n−1,
∴ bn=2(2n−1)⋅3n−1.
【考点】
数列递推式
等比数列的性质
【解析】
(Ⅰ)由已知的数列递推式得到Sn+1+1=3(Sn+1),即可说明{Sn+1}是首项为3,公比为3的等比数列;
(Ⅱ)由(Ⅰ)求得Sn,当n=1时,求得a1=S1=2.当n>1时,由an=Sn−Sn−1求得通项公式an;
(Ⅲ)由数列{bnan}是首项为1,公差为2的等差数列求其通项公式,代入an可得数列{bn}的通项公式.
【解答】
(1)证明:∵ Sn+1=3Sn+2,Sn+1+1=3(Sn+1),
又S1+1=3,
∴ {Sn+1}是首项为3
第29页 共32页 ◎ 第30页 共32页
,公比为3的等比数列;
(2)由(Ⅰ)可得Sn=3n−1,n∈N*.
当n=1时,a1=S1=2.
当n>1时,an=Sn−Sn−1=(3n−1)−(3n−1−1)
=3n−1(3−1)=2×3n−1.
故an=2×3n−1,n∈N*;
(Ⅲ)∵ 数列{bnan}是首项为1,公差为2的等差数列,
∴ bnan=1+2(n−1)=2n−1,
∴ bn=2(2n−1)⋅3n−1.
【答案】
解:(1)设M(x1,x12),N(x2,x22).
由OM⊥ON得x1x2+x12x22=0,
所以x1x2=−1.
因为x1=m,所以x2=−1m.
所以|OM|=m2+m4,
|ON|=m2+1m4.
所以n=S△OMN
=12|OM||ON|
=12×m2+m4×m2+1m4
=122+m2+1m2≥1.
所以当m=1时,△OMN面积取得最小值1.
(2)设B(x3,x32),C(x4,x42),
直线AB的方程为y−9=k1(x−3),
AC的方程为y−9=k2(x−3),
因为直线AB,AC与圆x2+(y−2)2=1相切,
所以|3k1−7|1+k12=|3k2−7|1+k22=1.
所以4k12−21k1+24=0,4k22−21k2+24=0.
所以k1,k2 是方程4k2−21k+24=0的两根.
所以k1+k2=214.
由方程组y=x2,y−9=k1(x−3),得x2−k1x−9+3k1=0.
所以x3+3=k1,同理可得:x4+3=k2.
所以直线BC的斜率为x42−x32x4−x3
=x4+x3=k1+k2−6=−34.
【考点】
直线与椭圆结合的最值问题
【解析】
(1)由OM⊥ON,确定M,N的坐标,表示出|OM|=m2+m4,|ON|=m2+1m4,从而可得△OMN的面积,利用基本不等式可求△OMN面积的最小值;
(2)设B(x3,x32),C(x4,x42),直线AB的方程为y−9=k1(x−3),AC的方程为y−9=k2(x−3),利用直线ABAC与圆x2+(y−2)2=1相切,建立方程,从而可得以k1,k2 是方程4k2−21k+24=0的两根,再联立方程组,利用韦达定理,可得直线BC的斜率,化简可得结论.
【解答】
解:(1)设M(x1,x12),N(x2,x22).
由OM⊥ON得x1x2+x12x22=0,
所以x1x2=−1.
因为x1=m,所以x2=−1m.
所以|OM|=m2+m4,
|ON|=m2+1m4.
所以n=S△OMN
=12|OM||ON|
=12×m2+m4×m2+1m4
=122+m2+1m2≥1.
所以当m=1时,△OMN面积取得最小值1.
第29页 共32页 ◎ 第30页 共32页
(2)设B(x3,x32),C(x4,x42),
直线AB的方程为y−9=k1(x−3),
AC的方程为y−9=k2(x−3),
因为直线AB,AC与圆x2+(y−2)2=1相切,
所以|3k1−7|1+k12=|3k2−7|1+k22=1.
所以4k12−21k1+24=0,4k22−21k2+24=0.
所以k1,k2 是方程4k2−21k+24=0的两根.
所以k1+k2=214.
由方程组y=x2,y−9=k1(x−3),得x2−k1x−9+3k1=0.
所以x3+3=k1,同理可得:x4+3=k2.
所以直线BC的斜率为x42−x32x4−x3
=x4+x3=k1+k2−6=−34.
【答案】
(1)设椭圆G:x2a2+y2b2=1(a>b>0),
可知ca=32,又因为a2=b2+c2,所以a2=4b2.
由定点M(1,12)在椭圆上可得1a2+14b2=1,故b2=12,a2=2.
所以椭圆G的方程为x2+4y2=2.
(2)当直线AB与x轴垂直时,设A(s, t)(s≠1),则B(s, −t).
由题意得:t−12s−1+−t−12s−1=1,即s=0.所以 直线AB的方程为x=0.
当直线AB不与x轴垂直时,可设直线AB为y=kx+m,A(x1, y1),B(x2, y2),
将y=kx+m代入x2+4y2=2得(1+4k2)x2+8kmx+4m2−2=0.
所以 x1+x2=−8km1+4k2,x1⋅x2=−4m2−21+4k2.
由直线MA与MB的斜率之和为1可得y1−12x1−1+y2−12x2−1=1①,
将y1=kx1+m和y2=kx2+m代入①,
并整理得(2k−1)x1x2+(m−k+12)(x1+x2)−2m=0②,
将x1+x2=−8km1+4k2,x1⋅x2=−4m2−21+4k2代入②
并整理得2km+2m2+2k+m−1=0,
分解因式可得(2k+2m+1)(m+1)=0,
因为直线AB:y=kx+m不经过点M(1,12),所以2k+2m+1≠0,故m=−1.
所以直线AB的方程为y=kx−1,经过定点(0, −1).
综上所述,直线AB经过定点(0, −1).
(Ⅲ) 由(Ⅱ)可得:△=32k2−8>0,k2>14.|AB|=1+k2|x1−x2|=1+k2⋅(x1+x2)2−4x1x2=1+k2⋅22⋅4k2−14k2+1.
因为 坐标原点O到直线AB的距离为11+k2,
所以△ABO的面积S=2⋅4k2−14k2+1(k2>14).
令4k2−1=t,则t>0,且S=2tt2+2=2t+2t≤222=12,
当且仅当t=2,即k=±32时,△ABO的面积S取得最大值12.
【考点】
直线与椭圆结合的最值问题
椭圆的标准方程
【解析】
(Ⅰ)由已知可知ca=32,结合a2=b2+c2,及点M(1,12)在椭圆上可求a,b进而可求椭圆方程
(Ⅱ)分类讨论:当直线AB与x轴垂直时,易求直线AB的方程;当直线AB不与x轴垂直时,设直线AB为y=kx+m,A(x1, y1),B(x2, y2),联立y=kx+m与x2+4y2=2,根据方程的根与系数关系可求x1+x2,x1x2,然后结合已知斜率关系即可求直线AB的方程,即可求解;
(Ⅲ) 由(Ⅱ)整理方程可求k的范围,结合弦长公式可求AB,然后利用点到直线的距离公式求出点O到直线AB的距离,代入可求△ABO的面积,利用基本不等式可求面积的最大值
【解答】
(1)设椭圆G:x2a2+y2b2=1(a>b>0),
可知ca=32,又因为a2=b2+c2,所以a2=4b2.
由定点M(1,12)在椭圆上可得1a2+14b2=1,故b2=12,a2=2.
所以椭圆G的方程为x2+4y2=2.
(2)当直线AB与x轴垂直时,设A(s, t)(s≠1),则B(s, −t).
由题意得:t−12s−1+−t−12s−1=1,即s=0.所以 直线AB的方程为x=0.
当直线AB不与x轴垂直时,可设直线AB为y=kx+m,A(x1, y1),B(x2, y2),
将y=kx+m代入x2+4y2=2得(1+4k2)x2+8kmx+4m2−2=0.
所以 x1+x2=−8km1+4k2,x1⋅x2=−4m2−21+4k2.
由直线MA与MB的斜率之和为1可得y1−12x1−1+y2−12x2−1=1①,
将y1=kx1+m和y2=kx2+m代入①,
并整理得(2k−1)x1x2+(m−k+12)(x1+x2)−2m=0②,
将x1+x2=−8km1+4k2,x1⋅x2=−4m2−21+4k2代入②
并整理得2km+2m2+2k+m−1=0,
分解因式可得(2k+2m+1)(m+1)=0,
因为直线AB:y=kx+m不经过点M(1,12),所以2k+2m+1≠0,故m=−1.
所以直线AB的方程为y=kx−1,经过定点(0, −1).
综上所述,直线AB经过定点(0, −1).
(Ⅲ) 由(Ⅱ)可得:△=32k2−8>0,k2>14.|AB|=1+k2|x1−x2|=1+k2⋅(x1+x2)2−4x1x2=1+k2⋅22⋅4k2−14k2+1.
因为 坐标原点O到直线AB的距离为11+k2,
所以△ABO的面积S=2⋅4k2−14k2+1(k2>14).
令4k2−1=t,则t>0,且S=2tt2+2=2t+2t≤222=12,
当且仅当t=2,即k=±32时,△ABO的面积S取得最大值12.
第29页 共32页 ◎ 第30页 共32页
【答案】
(1)∵ 1+3+9+...+3n−1=1×(1−3n)1−3=12(3n−1)<3n,不满足③,
则集合N={1, 3, 9, 27, ..., 3n}(n∈N*)“不可均分”.
(2)设B1={2015+1, 2015+2, ..., 2015+47},C1={2015+48, 2015+49, ..., 2015+93},
考虑到[(2015+48)+(2015+49)+...+(2015+93)]−[(2015+1)+(2015+2)+...+(2015+47)]=46×46−(2015+1)=100.
将B1中的2015+1与C1中的2015+51交换,得到集合B,C,
则得到的B,C满足条件①②③,
则集合A={2015+1, 2015+2, ..., 2015+93}“可均分”;
(Ⅲ)一方面,假设A={2015+1, 2015+2, ..., 2015+k}“可均分”,则存在B,C满足条件①②③,
∴ (2015+1)+(2015+2)+...+(2015+k)=2016k+k(k−1)2为偶数,
∴ k=4a或k=4a+1(a∈N*).
设k=4a+1,不妨设B中的元素个数大于等于2a+1,C中的元素个数小于等于2a,
于是B的元素之和SB≥(2015+1)+(2015+2)+...+[2015+(2a+1)],
C的元素之和SC≤[2015+(2a+2)]+[2015+(2a+3)]+...+[2015+(4a+1)],
整理得:(2015+1)+(2015+2)+...+[2015+(2a+1)]
≤[2015+(2a+2)]+[2015+(2a+3)]+...+[2015+(4a+1)],
即2016(2a+1)+(2a+1)⋅2a2≤2a(2017+2a)+2a(2a−1)2,
即4032a+2016+4a2+a≤4034a+4a2+2a2−a,
解得:a2≥504,即a≥23,
∴ k=4a(a∈N*)或k=4a+1(a≥23, a∈N*);
另一方面,当k=4a(a∈N*)时,A={2015+1, 2015+2, ..., 2015+k}中的连续四个必可分成两两一组,
其和相等;
∴ A={2015+1, 2015+2, ..., 2015+k}“可均分”;
当k=4a+1(a≥23, a∈N*)时,
由(Ⅱ)问可知A={2015+1, 2015+2, ..., 2015+k}的前93个数组成的集合“可均分”,
由前面的讨论知可将剩下的4p个元素分成和相等的两个不相交的子集,
即此时A={2015+1, 2015+2, ..., 2015+k}“可均分”.
综上,k=4a(a∈N*)或k=4a+1(a≥23, a∈N*).
【考点】
交、并、补集的混合运算
【解析】
(Ⅰ)根据“可均分”的定义进行判断即可;
(Ⅱ)结合可均分的定义进行证明;
(Ⅲ)根据“可均分”的定义进行求解.
【解答】
(1)∵ 1+3+9+...+3n−1=1×(1−3n)1−3=12(3n−1)<3n,不满足③,
则集合N={1, 3, 9, 27, ..., 3n}(n∈N*)“不可均分”.
(2)设B1={2015+1, 2015+2, ..., 2015+47},C1={2015+48, 2015+49, ..., 2015+93},
考虑到[(2015+48)+(2015+49)+...+(2015+93)]−[(2015+1)+(2015+2)+...+(2015+47)]=46×46−(2015+1)=100.
将B1中的2015+1与C1中的2015+51交换,得到集合B,C,
则得到的B,C满足条件①②③,
则集合A={2015+1, 2015+2, ..., 2015+93}“可均分”;
(Ⅲ)一方面,假设A={2015+1, 2015+2, ..., 2015+k}“可均分”,则存在B,C满足条件①②③,
∴ (2015+1)+(2015+2)+...+(2015+k)=2016k+k(k−1)2为偶数,
∴ k=4a或k=4a+1(a∈N*).
设k=4a+1,不妨设B中的元素个数大于等于2a+1,C中的元素个数小于等于2a,
于是B的元素之和SB≥(2015+1)+(2015+2)+...+[2015+(2a+1)],
C的元素之和SC≤[2015+(2a+2)]+[2015+(2a+3)]+...+[2015+(4a+1)],
整理得:(2015+1)+(2015+2)+...+[2015+(2a+1)]
≤[2015+(2a+2)]+[2015+(2a+3)]+...+[2015+(4a+1)],
即2016(2a+1)+(2a+1)⋅2a2≤2a(2017+2a)+2a(2a−1)2,
即4032a+2016+4a2+a≤4034a+4a2+2a2−a,
解得:a2≥504,即a≥23,
∴ k=4a(a∈N*)或k=4a+1(a≥23, a∈N*);
另一方面,当k=4a(a∈N*)时,A={2015+1, 2015+2, ..., 2015+k}中的连续四个必可分成两两一组,
其和相等;
∴ A={2015+1, 2015+2, ..., 2015+k}“可均分”;
当k=4a+1(a≥23, a∈N*)时,
由(Ⅱ)问可知A={2015+1, 2015+2, ..., 2015+k}的前93个数组成的集合“可均分”,
由前面的讨论知可将剩下的4p个元素分成和相等的两个不相交的子集,
即此时A={2015+1, 2015+2, ..., 2015+k}“可均分”.
综上,k=4a(a∈N*)或k=4a+1(a≥23, a∈N*).
第29页 共32页 ◎ 第30页 共32页