高考数学复习 17-18版 第2章 第10课 函数的图象

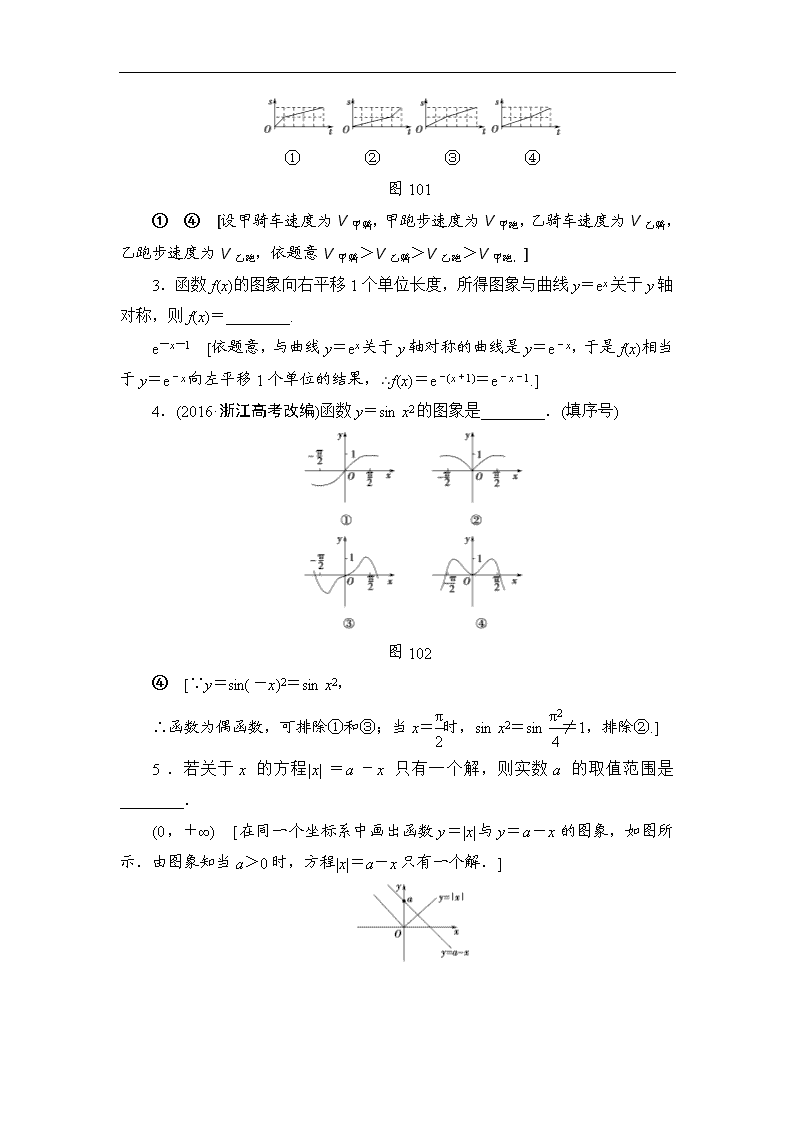
高考数学复习 17-18版 第2章 第10课 函数的图象

第 10 课函数的图象 [最新考纲] 要求 内容 A B C 函数的图象 √ 1．利用描点法作函数的图象 方法步骤：(1)确定函数的定义域； (2)化简函数的解析式； (3)讨论函数的性质(奇偶性、单调性、周期性、最值等)； (4)描点连线． 2．利用图象变换法作函数的图象 (1)平移变换 (2)对称变换 ①y＝f(x)的图象 ― ― ― ― ― ― → 关于x轴对称 y＝－f(x)的图象； ②y＝f(x)的图象 ― ― ― ― ― ― ―→ 关于y轴对称 y＝f(－x)的图象； ③y＝f(x)的图象 ― ― ― ― ― ― ―→ 关于原点对称 y＝－f(－x)的图象； ④y＝ax(a＞0 且 a≠1)的图象 ― ― ― ― ― ― ― ― ―→ 关于直线y＝x对称 y＝logax(a＞0 且 a≠1)的图象． (3)伸缩变换 ①y＝f(x)的图象 y＝f(ax)的图象； ②y＝f(x)的图象 ― ― ― ― ― ― ― ― ― ― ― ― ― ― ― ― ― ― ― ― ― ― ―→ a＞1，纵坐标伸长为原来的a倍，横坐标不变 0＜a＜1，纵坐标缩短为原来的a倍，横坐标不变 y＝af(x)的图象． (4)翻转变换 ①y＝f(x)的图象 ― ― ― ― ― ― ― ― ― ― ―→ x轴下方部分翻折到上方 x轴及上方部分不变 y＝|f(x)|的图象； ②y＝f(x)的图象 ― ― ― ― ― ― ― ― ― ― ― ― ― ― → y轴右侧部分翻折到左侧 原y轴左侧部分去掉，右侧不变 y＝f(|x|)的 图象． 1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”) (1)函数 y＝f(1－x)的图象，可由 y＝f(－x)的图象向左平移 1 个单位得 到．(　　) (2)函数 y＝f(x)的图象关于 y 轴对称即函数 y＝f(x)与 y＝f(－x)的图象关于 y 轴对称．(　　) (3)当 x∈(0，＋∞)时，函数 y＝f(|x|)的图象与 y＝|f(x)|的图象相同．(　　) (4)若函数 y＝f(x)满足 f(1＋x)＝f(1－x)，则函数 f(x)的图象关于直线 x＝1 对 称．(　　) [答案]　(1)×　(2)×　(3)×　(4)√ 2．(教材改编)甲、乙二人同时从 A 地赶往 B 地，甲先骑自行车到两地的中 点再改为跑步，乙先跑步到中点再改为骑自行车，最后两人同时到达 B 地．已 知甲骑车比乙骑车的速度快，且两人骑车速度均大于跑步速度．现将两人离开 A 地的距离 s 与所用时间 t 的函数关系用图象表示，则下列给出的四个函数图象中， 甲、乙的图象分别是________、________.(填序号) ①　　　　②　　　　③　　　　④ 图 10­1 ①　④　[设甲骑车速度为 V 甲骑，甲跑步速度为 V 甲跑，乙骑车速度为 V 乙骑， 乙跑步速度为 V 乙跑，依题意 V 甲骑＞V 乙骑＞V 乙跑＞V 甲跑．] 3．函数 f(x)的图象向右平移 1 个单位长度，所得图象与曲线 y＝ex 关于 y 轴 对称，则 f(x)＝________. e－x－1　[依题意，与曲线 y＝ex 关于 y 轴对称的曲线是 y＝e－x，于是 f(x)相当 于 y＝e－x 向左平移 1 个单位的结果，∴f(x)＝e－(x＋1)＝e－x－1.] 4．(2016·浙江高考改编)函数 y＝sin x2 的图象是________．(填序号) 图 10­2 ④　[∵y＝sin(－x)2＝sin x2， ∴函数为偶函数，可排除①和③；当 x＝π 2 时，sin x2＝sin π2 4 ≠1，排除②.] 5 ． 若 关 于 x 的 方 程 |x| ＝ a － x 只 有 一 个 解 ， 则 实 数 a 的 取 值 范 围 是 ________． (0，＋∞)　[在同一个坐标系中画出函数 y＝|x|与 y＝a－x 的图象，如图所 示．由图象知当 a＞0 时，方程|x|＝a－x 只有一个解．] 作函数的图象 　作出下列函数的图象： (1)y＝(1 2 )|x|；(2)y＝|log2(x＋1)|； (3)y＝2x－1 x－1 ；(4)y＝x2－2|x|－1. [解]　(1)先作出 y＝(1 2 )x 的图象，保留 y＝(1 2 )x 图象中 x≥0 的部分，再 作出 y＝(1 2 )x 的图象中 x＞0 部分关于 y 轴的对称部分，即得 y＝(1 2 )|x|的图 象，如图①实线部分． ①　　　　　　　② (2)将函数 y＝log2x 的图象向左平移一个单位，再将 x 轴下方的部分沿 x 轴翻 折上去，即可得到函数 y＝|log2(x＋1)|的图象，如图②. (3)∵y＝2＋ 1 x－1 ，故函数图象可由 y＝1 x 图象向右平移 1 个单位，再向上平 移 2 个单位得到，如图③. ③　　　　　　　　　④ (4)∵y＝Error!且函数为偶函数，先用描点法作出[0，＋∞)上的图象，再根 据对称性作出(－∞，0)上的图象，得图象如图④. [规律方法]　画函数图象的一般方法 (1)直接法．当函数表达式(或变形后的表达式)是熟悉的基本函数时，就可根 据这些函数的特征直接作出； (2)图象变换法．若函数图象可由某个基本函数的图象经过平移、翻折、对 称得到，可利用图象变换作出． 易错警示：注意平移变换与伸缩变换的顺序对变换单位及解析式的影响． [变式训练 1]　分别画出下列函数的图象： (1)y＝|lg x|；(2)y＝sin|x|. [解]　(1)∵y＝|lg x|＝Error! ∴函数 y＝|lg x|的图象，如图①. (2)当 x≥0 时，y＝sin|x|与 y＝sin x 的图象完全相同，又 y＝sin|x|为偶函数， 图象关于 y 轴对称，其图象如图②. 识图与辨图 　(1)(2016· 全国卷Ⅰ改编)函数 y＝2x2－e|x|在[－2,2]的图象大致为 ________．(填序号) 图 10­3 (2)如图 10­4，长方形 ABCD 的边 AB＝2，BC＝1，O 是 AB 的中点．点 P 沿 着边 BC，CD 与 DA 运动，记∠BOP＝x.将动点 P 到 A，B 两点距离之和表示为 x 的函数 f(x)，则 y＝f(x)的图象大致为________．(填序号) 【导学号：62172054】 图 10­4 ①　　　②　　　③　　　　④ (1)④　(2)②　[(1)∵f(x)＝2x 2－e|x|，x∈[－2,2]是偶函数，又 f(2)＝8－e 2∈ (0,1)，故排除①，②.设 g(x)＝2x2－ex，则 g′(x)＝4x－ex.又 g′(0)＜0，g′(2)＞ 0，∴g(x)在(0,2)内至少存在一个极值点，∴f(x)＝2x2－e|x|在(0,2)内至少存在一个 极值点，排除③. (2)当 x∈[0，π 4]时，f(x)＝tan x＋ 4＋tan2x，图象不会是直线段，从而排除 ①，③. 当 x∈[π 4 ，3π 4 ]时，f(π 4 )＝f(3π 4 )＝1＋ 5，f(π 2 )＝2 2. ∵2 2<1＋ 5，∴f(π 2 )0)的图象， 使它与直线 y＝kx－1(x>0)的交点个数为 2 即可． 当直线 y＝kx－1 与 y＝ln x 的图象相切时，设切点为(m，ln m)，又 y＝ln x 的导数为 y′＝1 x ， 即 km－1＝ln m，k＝1 m ，解得 m＝1，k＝1， 可得函数 y＝ln x(x>0)的图象过(0，－1)点的切线的斜率为 1， 结合图象可知 k∈(0,1)时两函数图象有两个交点．] ☞ 角度 4　求不等式的解集 　函数 f(x)是定义在[－4,4]上的偶函数，其在[0,4]上的图象如图 10­7 所示，那么不等式 f(x) cos x ＜0 的解集为________． 图 10­7 (－π 2 ，－1)∪(1，π 2)　[在(0，π 2)上，y＝cos x＞0，在(π 2 ，4)上，y＝cos x＜0. 由 f(x)的图象知在(1，π 2)上 f(x) cos x ＜0， 因为 f(x)为偶函数，y＝cos x 也是偶函数， 所以 y＝ f(x) cos x 为偶函数， 所以 f(x) cos x ＜0 的解集为(－π 2 ，－1)∪(1，π 2).] [规律方法]　函数图象应用的常见题型与求解方法 (1)研究函数性质： ①根据已知或作出的函数图象，从最高点、最低点，分析函数的最值、极 值． ②从图象的对称性，分析函数的奇偶性． ③从图象的走向趋势，分析函数的单调性、周期性． ④从图象与 x 轴的交点情况，分析函数的零点等． (2)研究方程根的个数或由方程根的个数确定参数的值(范围)：构造函数，转 化为两函数图象的交点个数问题，在同一坐标系中分别作出两函数的图象，数形 结合求解． (3)研究不等式的解：当不等式问题不能用代数法求解，但其对应函数的图 象可作出时，常将不等式问题转化为两函数图象的上、下关系问题，从而利用数 形结合求解． [思想与方法] 1．识图 对于给定函数的图象，要从图象的左右、上下分布范围、变化趋势、对称性 等方面研究函数的定义域、值域、单调性、奇偶性、周期性，注意图象与函数解 析式中参数的关系． 2．用图 借助函数图象，可以研究函数的定义域、值域、单调性、奇偶性、对称性等 性质．利用函数的图象，还可以判断方程 f(x)＝g(x)的解的个数，求不等式的解 集等． [易错与防范] 1．图象变换是针对自变量 x 而言的，如从 f(－2x)的图象到 f(－2x＋1)的图 象是向右平移1 2 个单位，先作如下变形 f(－2x＋1)＝f(－2(x－1 2))，可避免出错． 2．明确一个函数的图象关于 y 轴对称与两个函数的图象关于 y 轴对称的不 同，前者是自身对称，且为偶函数，后者是两个不同函数的对称关系． 3．当图形不能准确地说明问题时，可借助“数”的精确，注重数形结合思 想的运用． 课时分层训练(十) A 组　基础达标 (建议用时：30 分钟) 一、填空题 1．为了得到函数 y＝2x－2 的图象，可以把函数 y＝2x 的图象上所有的点向 右平移________个单位长度． 1　[因为 y＝2x－2＝2(x－1)，所以只需将函数 y＝2x 的图象上所有的点向右 平移 1 个单位长度，即可得到 y＝2(x－1)＝2x－2 的图象．] 2．小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间，后 为了赶时间加快速度行驶．与以上事件吻合得最好的图象是________．(填序号) ①　　　　②　　　　③　　　　④ 图 10­8 ③　[出发时距学校最远，先排除①，中途堵塞停留，距离没变，再排除④， 堵塞停留后比原来骑得快，因此排除②.] 3．(2017·南京模拟)函数 y＝(x3－x)2|x|的图象大致是________．(填序号) 【导学号：62172056】 ①　　　　②　　　　③　　　　④ 图 10­9 ②　[由于函数 y＝(x3－x)2|x|为奇函数，故它的图象关于原点对称，当 0＜x＜ 1 时，y＜0；当 x>1 时，y>0.] 4．已知函数 f(x)＝Error!若关于 x 的方程 f(x)＝k 有两个不等的实数根，则 实数 k 的取值范围是________． (0,1]　[作出函数 y＝f(x)与 y＝k 的图象，如图所示： 由图可知 k∈(0,1]．] 5．已知函数 f(x)＝|x－2|＋1，g(x)＝kx.若方程 f(x)＝g(x)有两个不相等的实根， 则实数 k 的取值范围是________． (1 2 ，1)　[先作出函数 f(x)＝|x－2|＋1 的图象，如图 所示，当直线 g(x)＝kx 与射线 AB 平行时斜率为 1，当直 线 g(x)＝kx 过 A 点时斜率为1 2 ，故 f(x)＝g(x)有两个不相 等的实根时，k 的取值范围为(1 2 ，1).] 6．已知函数 f(x)的图象如图 10­10 所示，则函数 g(x)＝log 2f(x)的定义域是 ________． 图 10­10 (2,8]　[当 f(x)＞0 时，函数 g(x)＝log 2f(x)有意义， 由函数 f(x)的图象知满足 f(x)＞0 时，x∈(2,8]．] 7．如图 10­11，定义在[－1，＋∞)上的函数 f(x)的图象由一条线段及抛物线 的一部分组成，则 f(x)的解析式为________. 【导学号：62172057】 图 10­11 f(x)＝Error!　[当－1≤x≤0 时， 设解析式为 y＝kx＋b， 则Error!得Error!∴y＝x＋1. 当 x＞0 时，设解析式为 y＝a(x－2)2－1. ∵图象过点(4,0)，∴0＝a(4－2)2－1， 得 a＝1 4 ，即 y＝1 4(x－2)2－1. 综上，f(x)＝Error!] 8．(2015·安徽高考)在平面直角坐标系 xOy 中，若直线 y＝2a 与函数 y＝|x－ a|－1 的图象只有一个交点，则 a 的值为________． －1 2 　[函数 y＝|x－a|－1 的图象如图所示，因为直线 y＝ 2a 与函数 y＝|x－a|－1 的图象只有一个交点，故 2a＝－1， 解得 a＝－1 2.] 9．如图 10­12，函数 f(x)的图象为折线 ACB，则不等式 f(x)≥log2(x＋1)的解 集是________． 图 10­12 {x|－10 在 R 上恒成立，求 m 的取值范围． [解]　(1)令 F(x)＝|f(x)－2|＝|2x－2|， G(x)＝m，画出 F(x)的图象如图所示： 由图象看出，当 m＝0 或 m≥2 时，函数 F(x)与 G(x)的图象只有一个交点， 原方程有一个解； 当 00)，H(t)＝t2＋t， 因为 H(t)＝(t＋1 2 )2－1 4 在区间(0，＋∞)上是增函数， 所以 H(t)>H(0)＝0. 因此要使 t2＋t>m 在区间(0，＋∞)上恒成立，应有 m≤0，即所求 m 的取值 范围为(－∞，0]． 4．已知函数 f(x)的图象与函数 h(x)＝x＋1 x ＋2 的图象关于点 A(0,1)对称． (1)求函数 f(x)的解析式； (2)若 g(x)＝f(x)＋ a x ，g(x)在区间(0,2]上的值不小于 6，求实数 a 的取值范 围． [解]　(1)设 f(x)图象上任一点坐标为(x，y)， ∵点(x，y)关于点 A(0,1)的对称点(－x,2－y)在 h(x)的图象上， ∴2－y＝－x＋ 1 －x ＋2， ∴y＝x＋1 x ，即 f(x)＝x＋1 x. (2)由题意 g(x)＝x＋a＋1 x ， 且 g(x)＝x＋a＋1 x ≥6，x∈(0,2]． ∵x∈(0,2]，∴a＋1≥x(6－x)， 即 a≥－x2＋6x－1. 令 q(x)＝－x2＋6x－1，x∈(0,2]， q(x)＝－x2＋6x－1＝－(x－3)2＋8， ∴x∈(0,2]时，q(x)max＝q(2)＝7， 故 a 的取值范围为[7，＋∞)．