高中数学学业水平考试模拟卷（五）

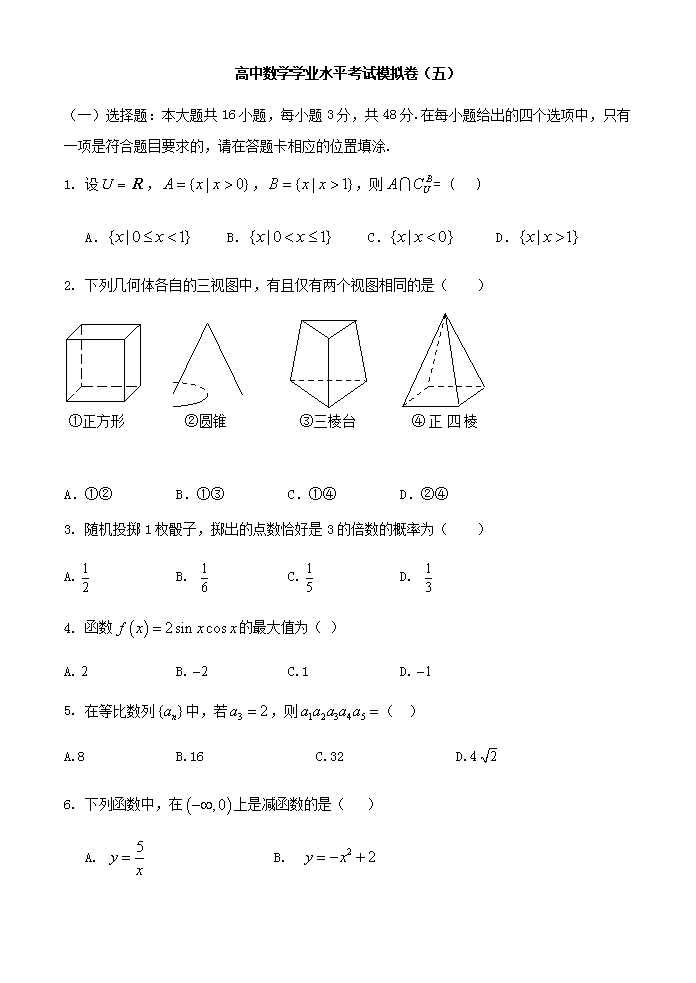
高中数学学业水平考试模拟卷（五）

高中数学学业水平考试模拟卷（五）‎ ‎（一）选择题：本大题共16小题，每小题3分，共48分.在每小题给出的四个选项中，只有一项是符合题目要求的，请在答题卡相应的位置填涂.‎ ‎1. 设，，，则= ( ) ‎ A． B． C． D．‎ ‎2. 下列几何体各自的三视图中，有且仅有两个视图相同的是（ ）‎ ‎①正方形 ‎②圆锥 ‎③三棱台 ‎④正四棱锥 A．①② B．①③ C．①④ D．②④‎ ‎3. 随机投掷1枚骰子，掷出的点数恰好是3的倍数的概率为（ ）‎ A. B. C. D. ‎ ‎4. 函数的最大值为（ ）‎ A. B. C.1 D.‎ ‎5. 在等比数列中，若，则（ ）‎ A.8 B.16 C.32 D.4‎ ‎6. 下列函数中，在上是减函数的是（ ）‎ A. B. ‎ C. D. ‎ ‎7. 设是直线，，是两个不同的平面，则（ ）‎ A. 若，，则 B. 若，，则 C. 若，，则 D. 若，，则 ‎8. 某单位有职工750人，其中青年职工350人，中年职工250人，老年职工150人，为了了解该单位职工的健康情况，用分层抽样的方法从中抽取样本 . 若样本中的青年职工为7人，则样本容量为（ ）‎ A.7 B.15 C.25 D.35‎ ‎9. 的值为（ ）‎ A．1 B． C． D．‎ ‎10. 设是等差数列，= （ ）‎ ‎ A．31 B．32 C．33 D．34‎ ‎11. 已知幂函数的图象过点，则它的单调递增区间为（ ）‎ A.（1,+∞） B. (-∞,0) C.(-∞, +∞） D. ［0, +∞)‎ ‎12. 圆⊙：，与圆⊙：的位置关系是（ ） ‎ A．外切 B．内切 C．相交 D．相离 输入 开始 输出 结束 是 否 ‎13. 执行如图所示的程序框图，若输入的值为6，则输出 的值为（ ）‎ A. 105 B. 16 ‎ ‎ C. 15 D. 1‎ ‎14. 在△中，若，，，则 A. B. C. D. ‎ ‎15. 设变量满足约束条件则目标函数的最小值为 （ ）‎ ‎ A．7 B．8 C．10 D．23‎ ‎16. 设，为奇函数，且，则（ ）‎ A. B. C. D. ‎ ‎（二）填空题：本大题共4小题，每小题4分，共16分.请把答案写在答题卡相应的位置上.‎ ‎17. 若直线与直线互相垂直，则实数=______‎ ‎18. 已知，，和的夹角为，则为 ‎ O ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎0.04‎ 频率/组距 时间/小时 ‎0.08‎ ‎0.10‎ ‎0.12‎ ‎0.16‎ ‎19. 某校对学生在一周中参加社会实践活动时间进行调查，现从中抽取一个容量为n的样本加以分析，其频率分布直方图如图所示，已知时间不超过2小时的人数为12人，则n= ．‎ ‎20. 已知函数在R上为偶函数，当时，，则＜0解集是 .‎ ‎（三）解答题：本大题共5小题．满分36分．解答应写出文字说明、证明过程或演算步骤．‎ ‎21. （5分）已知，试判断函数的奇偶性并证明.‎ ‎22. （6分）袋中有标号为1、2、3、4、5的5个球，从中随机取出两个球.‎ ‎（1）写出所有的基本事件；‎ ‎（2）求所取出的两个球的标号之和大于5的概率.‎ ‎23. （7分）如图，在多面体ABCDEF中，四边形ABCD是矩形，AB//EF，，平面 ‎.‎ ‎（1）若G点是DC中点，求证：.‎ ‎（2）求证：.‎ ‎24. （8分）在中，角的对边分别为．‎ ‎（1）求；‎ ‎（2）若，且，求．‎ ‎25. （10分）已知为等比数列，且.‎ ‎（1）若，求；（2）设数列的前项和为，求.‎ ‎ ‎ ‎ ‎ 参考答案 ‎（一）选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B ‎ D D ‎ C C ‎ A A B C B 题号 ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ 答案 D A C B A D ‎（二）填空题 ‎17. 1 18. 6 19. 150 20. ‎ ‎（三）解答题 ‎21. 解：要使函数有意义，必须满足，即∴‎ ‎∴定义域为，关于原点对称.‎ 又∵，∴是奇函数 ‎22. 解：（1）随机取两个球的基本事件为（1,2），（1,3），（1,4），（1,5），（2,3），（2,4），（2,5），（3,4），（3,5），（4,5）.‎ ‎（2）两球标号之和大于5的有（1,5），（2,3），（2,4），（2,5），（3,4），（3,5），（4,5），共有7个，所以所求概率为. ‎ ‎23. 解：（1）‎ ‎∴四边形为平行四边形，∴.‎ 又，，.‎ ‎（2）（1）‎ ‎，‎ ‎24. 解：（1）‎ ‎ 又， 解得．‎ ‎ ，是锐角 ．‎ ‎（2）， ， ．‎ ‎ 又， ，． ． ．‎ ‎25. 解：设，由题意，解之得，进而 ‎（1）由=，解得. ‎ ‎（2），∴.‎