高中数学必修3教案：2_2用样本估计总体（一） (2)

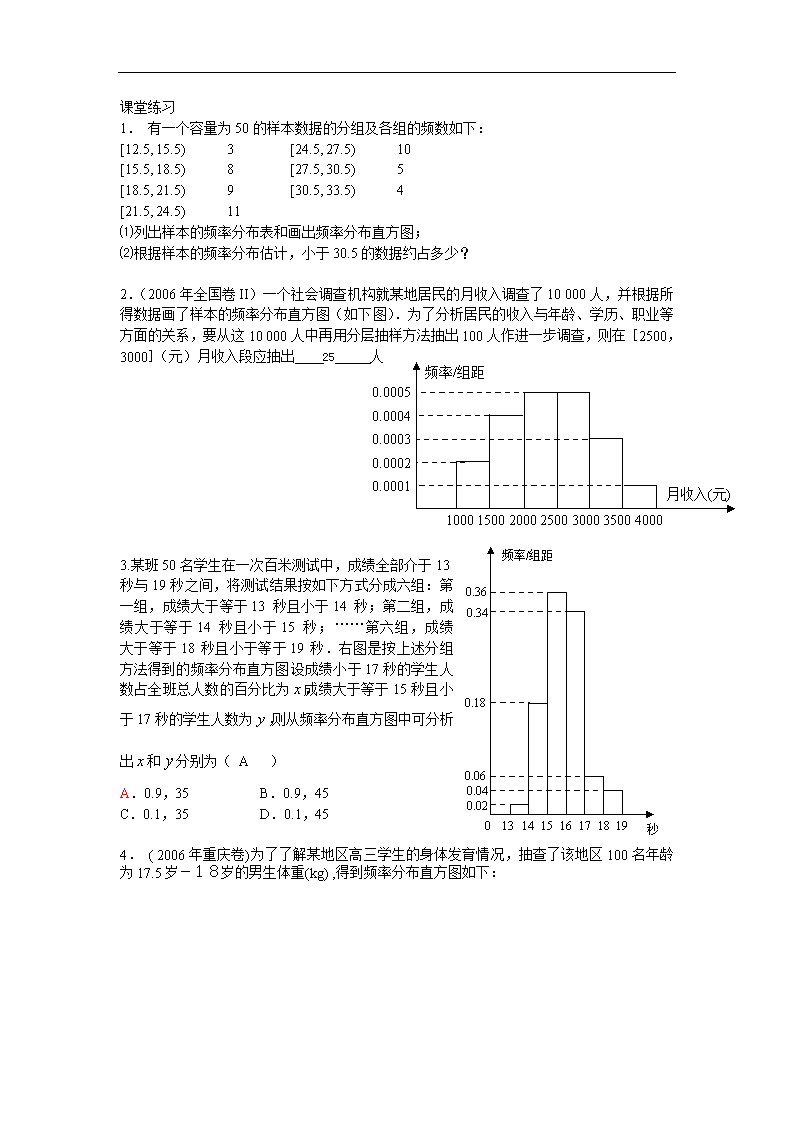
高中数学必修3教案：2_2用样本估计总体（一） (2)

‎2.2用样本估计总体（一） 知识探究(一):频率分布表 ‎【问题】 我国是世界上严重缺水的国家 之一，城市缺水问题较为突出，某市政 府为了节约生活用水，计划在本市试行 居民 生活用水定额管理，即确定一个居 民月用水量标准a，用水量不超过a的部 分按平价收费，超出a的部分按议价收费. 通过抽样调查，获得100位居民2007年的 月均用水量如下表（单位：t）： ‎3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6 ‎3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4 ‎3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8 ‎3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1 ‎3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3 ‎3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0 ‎2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3 ‎2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4 ‎2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4 ‎2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2 思考1：上述100个数据中的最大值和最小值分别是什么？由此说明样本数据的变化范围是什么？ 0.2～4.3 思考2：样本数据中的最大值和最小值的差称为极差.如果将上述100个数据按组距为0.5进行分组，那么这些数据共分为多少组？ (4.3-0.2)÷0.5=8.2 思考3：以组距为0.5进行分组，上述100个数据共分为9组，各组数据的取值范围可以如何设定？[0，0.5)，[0.5，1)，[1，1.5)，…，[4，4.5]. 思考4：如何统计上述100个数据在各组中的频数？如何计算样本数据在各组中的频率？你能将这些数据用表格反映出来吗？ ‎ 思考5：上表称为样本数据的频率分布表，由此可以推测该市全体居民月均用水量分布的大致情况，给市政府确定居民月用水量标准提供参考依据，这里体现了一种什么统计思想？ 用样本的频率分布估计总体分布. 思考6：如果市政府希望85%左右的居民每月的用水量不超过标准，根据上述频率分布表，你对制定居民月用水量标准（即a的取值）有何建议？ ‎88%的居民月用水量在3t以下，可建议取a=3. 思考7：在实际中，取a=3t一定能保证85%以上的居民用水不超标吗？哪些环节可能会导致结论出现偏差？ 分组时，组距的大小可能会导致结论出现偏差，实践中，对统计结论是需要进行评价的. 思考8：对样本数据进行分组，其组数是由哪些因素确定的？ 思考9：对样本数据进行分组，组距的确定没有固定的标准，组数太多或太少，都会影响我们了解数据的分布情况.数据分组的组数与样本容量有关，一般样本容量越大，所分组数越多. 思考10：一般地，列出一组样本数据的频率分布表可以分哪几个步骤进行？ 第一步，求极差. 第二步，决定组距与组数. 第三步，确定分点，将数据分组. 第四步，列频率分布表. 知识探究(二):频率分布直方图 思考1：为了直观反映样本数据在各组中的分布情况，我们将上述频率分布表中的有关信息用下面的图形表示： 思考2： 频率分布直方图中 小长方形的面积表示什么？小长方形的面积表示该组的频率． 所有小长方形的面积和＝？所有小长方形的面积和＝1． 思考3：频率分布直方图非常直观地表明了样本数据的分布情况，使我们能够看到频率分布表中看不太清楚的数据模式，但原始数据不能在图中表示出来.你能根据上述频率分布直方图指出居民月均用水量的一些数据特点吗？ ‎ (1)居民月均用水量的分布是“山峰”状的，而且是“单峰”的； ‎(2)大部分居民的月均用水量集中在一个中间值附近，只有少数居民的月均用水量很多或很少； ‎(3)居民月均用水量的分布有一定的对称性等. 思考4：样本数据的频率分布直方图是根据频率分布表画出来的，一般地，频率分布 直方图的作图步骤如何？‎ 第一步，画平面直角坐标系. ‎ 第二步，在横轴上均匀标出各组分点，在纵轴上标出单位长度.‎ 第三步，以组距为宽，各组的频率与组距的商为高，分别画出各组对应的小长方形.‎ 课堂练习 ‎1． 有一个容量为50的样本数据的分组及各组的频数如下：‎ ‎[12.5, 15.5) 3 [24.5, 27.5) 10‎ ‎[15.5, 18.5) 8 [27.5, 30.5) 5‎ ‎[18.5, 21.5) 9 [30.5, 33.5) 4‎ ‎[21.5, 24.5) 11‎ ‎⑴列出样本的频率分布表和画出频率分布直方图；‎ ‎⑵根据样本的频率分布估计，小于30.5的数据约占多少？ ‎ ‎0.0001‎ ‎0.0002‎ ‎0.0003‎ ‎0.0004‎ ‎0.0005‎ ‎1000 1500 2000 2500 3000 3500 4000‎ 月收入(元)‎ 频率/组距 ‎2．（2006年全国卷II）一个社会调查机构就某地居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图（如下图）．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，则在［2500，3000］（元）月收入段应抽出 25 人 ‎0‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎18‎ ‎19‎ 秒 频率/组距 ‎0.36‎ ‎0.34‎ ‎0.18‎ ‎0.06‎ ‎0.04‎ ‎0.02‎ ‎3.某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；第六组，成绩大于等于18秒且小于等于19秒．右图是按上述分组方法得到的频率分布直方图．设成绩小于17秒的学生人数占全班总人数的百分比为，成绩大于等于15秒且小于17秒的学生人数为，则从频率分布直方图中可分析出和分别为（ A ）‎ A．0.9，35 B．0.9，45‎ C．0.1，35 D．0.1，45‎ ‎4． ( 2006年重庆卷)为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁－１８岁的男生体重(kg) ,得到频率分布直方图如下：‎ 根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是 ( C)‎ ‎(A)20 (B)30 (C)40 （D）50‎ ‎5.（广东文7、艺术理6）下面左图是某县参加2007年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A1、A2、…、A10（如A2表示身高（单位：cm）（150，155）内的学生人数）.右图是统计左图中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~‎180cm(含‎160cm,不含‎180cm)的学生人数，那么在流程图中的判断框内应填写的条件是（B）‎ A.i<9 B. i<‎8 C. i<7 D. i<6‎ ‎0.3‎ ‎0.1‎ ‎4.3‎ ‎4.4‎ ‎4.5‎ ‎4.6‎ ‎4.7‎ ‎4.8‎ ‎4.9‎ ‎5.0‎ ‎5.1‎ ‎5.2‎ 视力 ‎6.为了解某校高三学生的视力情况，随机地抽查了该 校100名高三学生的视力情况，得到频率分布直方图，‎ 如右，由于不慎将部分数据丢失，但知道前4组的频 数成等比数列，后6组的频数成等差数列，设最大频 率为a，视力在4.6到5.0之间的学生数为b，则a, b 的值分别为（ A ）‎ A．0,27,78 B．0,27,83‎ C．2.7,78 D．2.7,83‎ 小结作业 ‎1.频率分布是指一个样本数据在各个小范围内所占比例的大小，总体分布是指总体取值的频率分布规律.我们通常用样本的频率分布表或频率分布直方图去估计总体的分布.‎ ‎2.频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息.‎ ‎3.样本数据的频率分布表和频率分布直方图，是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律，它可以让我们更清楚的看到整个样本数据的频率分布情况，并由此估计总体的分布情况.‎ 作业：《习案》作业十八