2019高考数学（理）冲刺大题提分（讲义+练习）大题精做9 圆锥曲线：范围（最值）问题（理）

2019高考数学（理）冲刺大题提分（讲义+练习）大题精做9 圆锥曲线：范围（最值）问题（理）

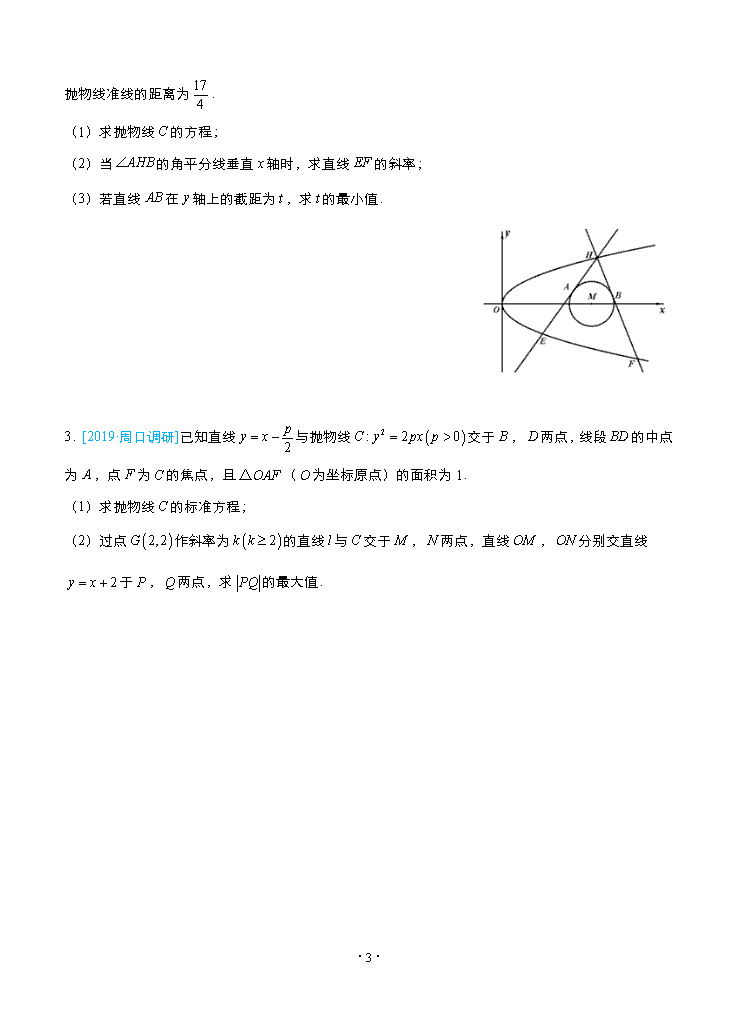
圆锥曲线：范围（最值）问题 大题精做九 精选大题 ‎[2019·江南十校]已知椭圆，为其短轴的一个端点，，分别为其左右两个 焦点，已知三角形的面积为，且．‎ ‎（1）求椭圆的方程；‎ ‎（2）若动直线与椭圆交于，，为线段的中点，‎ 且，求的最大值．‎ ‎【答案】（1）；（2）．‎ ‎【解析】（1）由，，‎ ‎，‎ 结合，，‎ 故椭圆的方程为．‎ 另解：依题意：，，‎ 解得，，故椭圆的方程为．‎ ‎（2）联立．‎ 且，；‎ 依题意，‎ ‎·6·‎ 化简得：（∵）；‎ 设，由，‎ 又，解得，‎ ‎，‎ ‎．当且仅当，即时，的最大值为．‎ 模拟精做 ‎1．[2019·柳州模拟]已知点，直线，为平面内的动点，过点作直线的垂线，垂足为点，且．‎ ‎（1）求动点的轨迹的方程；‎ ‎（2）过点作直线（与轴不重合）交轨迹于，两点，求三角形面积的取值范围．（为坐标原点）‎ ‎2．[2019·雷州期末]如图，已知抛物线和，过抛线上一点作两条直线与相切于、两点，分别交抛物线于、两点，圆心点 ‎·6·‎ 到抛物线准线的距离为．‎ ‎（1）求抛物线的方程；‎ ‎（2）当的角平分线垂直轴时，求直线的斜率；‎ ‎（3）若直线在轴上的截距为，求的最小值．‎ ‎3．[2019·周口调研]已知直线与抛物线交于，两点，线段的中点为，点为的焦点，且（为坐标原点）的面积为1．‎ ‎（1）求抛物线的标准方程；‎ ‎（2）过点作斜率为的直线与交于，两点，直线，分别交直线于，两点，求的最大值．‎ ‎·6·‎ 答案与解析 ‎1．【答案】（1）；（2）．‎ ‎【解析】（1）设动点，则，‎ 由，，‎ 即，，化简得．‎ ‎（2）由（1）知轨迹的方程为，当直线斜率不存在时，，‎ ‎，‎ 当直线斜率存在时，设直线方程为，设，，‎ 由，得．‎ 则，，，‎ ‎，‎ 令，则，‎ 令，则，当时，，‎ 在上单调递增，，，‎ 综上所述，三角形面积的取值范围是．‎ ‎2．【答案】（1）；（2）；（3）．‎ ‎【解析】（1）∵点到抛物线准线的距离为，∴，即抛物线的方程为．‎ ‎·6·‎ ‎（2）∵当的角平分线垂直轴时，点，∴，‎ 设，，∴，∴，‎ ‎∴．．‎ ‎（3）设点，，．‎ 以为圆心，为半径的圆方程为，……①‎ 方程：．……②‎ ‎①-②得：直线的方程为．‎ 当时，直线在轴上的截距，‎ ‎∵关于的函数在单调递增，∴．‎ ‎3．【答案】（1）；（2）．‎ ‎【解析】（1）设，，则．‎ 由，两式相减，得．‎ ‎∴，所以点的纵坐标为，‎ ‎∴的面积，解得．故所求抛物线的标准方程为．‎ ‎（2）直线的方程为．‎ 由方程组，得．‎ 设，，则，．‎ 直线的方程为，代入，解得，所以．‎ 同理得．‎ ‎·6·‎ 所以 ‎．‎ 因为，所以，所以当，即时，取得最大值．‎ ‎·6·‎