2019年高考理科数学考前30天--计算题专训（十七）

2019年高考理科数学考前30天--计算题专训（十七）

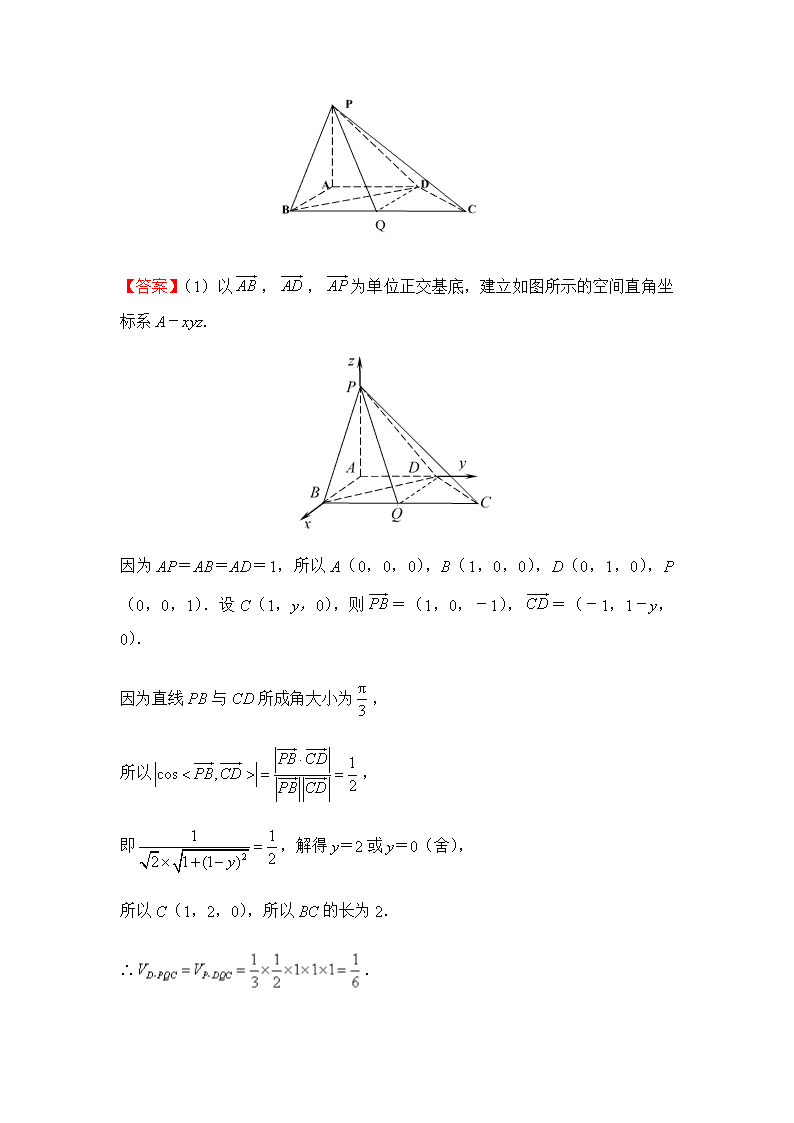
‎2019年高考理科数学考前30天--计算题专训（十七）‎ ‎17．（本小题满分12分）‎ 中，角，，的对边分别为，，，且．‎ ‎（1）求角的大小；‎ ‎（2）若，边上的中线，求的面积．‎ ‎【答案】（1），由正弦定理，得，‎ ‎，，‎ ‎，‎ ‎，‎ ‎，，，∴．‎ ‎（2）在中，由余弦定理得：，‎ 即，解得，‎ ‎．‎ ‎18．（本小题满分12分）‎ 某学校依次进行A、B两科考试，当A科合格时，才可考B科，且两科均有一次补考机会，两科都合格方通过．甲同学参加考试，已知他每次考A科合格的概率均为，每次考B科合格的概率均为．假设他不放弃每次考试机会，且每次考试互不影响．‎ ‎（1）求甲恰好3次考试通过的概率；‎ ‎（2）记甲参加考试的次数为X，求X的分布列和均值．‎ ‎【答案】（1）甲恰好3次通过考试有两种情况，第一种情况是第一次A科通过，第二次B科不过，第三次B科通过；第二种情况是第一次A科没通过，第二次A科通过，第三次B科通过，‎ ‎．‎ ‎（2）由题意得、、，；‎ ‎；‎ ‎，‎ 则的分布列为：‎ ‎2‎ ‎3‎ ‎4‎ ‎．‎ ‎19．（本小题满分12分）‎ 如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AB⊥AD，AD∥BC，AP＝AB＝AD＝1，直线PB与CD所成角的大小为．‎ ‎（1）若Q是BC的中点，求三棱锥D－PQC的体积；‎ ‎（2）求二面角B－PD－A的余弦值．‎ ‎【答案】（1）以，，为单位正交基底，建立如图所示的空间直角坐标系A－xyz．‎ 因为AP＝AB＝AD＝1，所以A（0，0，0），B（1，0，0），D（0，1，0），P（0，0，1）．设C（1，y，0），则＝（1，0，－1），＝（－1，1－y，0）．‎ 因为直线PB与CD所成角大小为，‎ 所以，‎ 即，解得y＝2或y＝0（舍），‎ 所以C（1，2，0），所以BC的长为2．‎ ‎∴．‎ ‎（2）设平面PBD的一个法向量为n1＝（x，y，z）．‎ 因为＝（1，0，－1），＝（0，1，－1），‎ 则，即，‎ 令x＝1，则y＝1，z＝1，所以n1＝（1，1，1）．‎ 因为平面PAD的一个法向量为n2＝（1，0，0），‎ 所以，‎ 所以，由图可知二面角B－PD－A的余弦值为．‎ ‎20．（本小题满分12分）‎ 已知函数．‎ ‎（1）当时，求的最大值与最小值；‎ ‎（2）如果函数有三个不同零点，求实数的取值范围．‎ ‎【答案】（1）因为，‎ 所以，‎ 令得，，，的变化如下表：‎ ‎－1‎ ‎2‎ ‎0‎ ‎－‎ ‎0‎ ‎＋‎ 在上的最小值是，‎ 因为，，，‎ 所以在上的最大值是．‎ ‎（2），‎ 所以或，‎ 设，则，时，，时，，‎ 所以在上是增函数，在上是减函数，，‎ 且，，，，‎ ‎①当时，即时，没有实根，方程有1个实根；‎ ‎②当时，即时，有1个实根为零，方程有1个实根；‎ ‎③当时，即时，有2不等于零的实根，方程有3个实根．‎ 综上可得，时，方程有3个实根．‎ ‎21．（本小题满分12分）‎ 如图所示，是抛物线：的焦点，在x轴上（其中i＝1，2，3，…，n），的坐标为且，在抛物线上，且在第一象限是正三角形．‎ ‎（1）证明：数列是等差数列；‎ ‎（2）记的面积为，证明：．‎ ‎【答案】（1）由题意知，，所以的方程是，‎ 代入抛物线可得，则，（舍），即，‎ ‎，，，又设，，‎ 是等边三角形，代入抛物线得：‎ ‎，两式相减得：‎ ‎，且，‎ 所以，，‎ 所以数列是等差数列，其中首项为，公差是．‎ ‎（2）由（1），‎ ‎，‎ ‎．‎