- 2021-06-20 发布 |
- 37.5 KB |
- 18页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江苏省苏州市2019-2020学年高二下学期学业质量阳光指标调研数学试题 Word版含答案
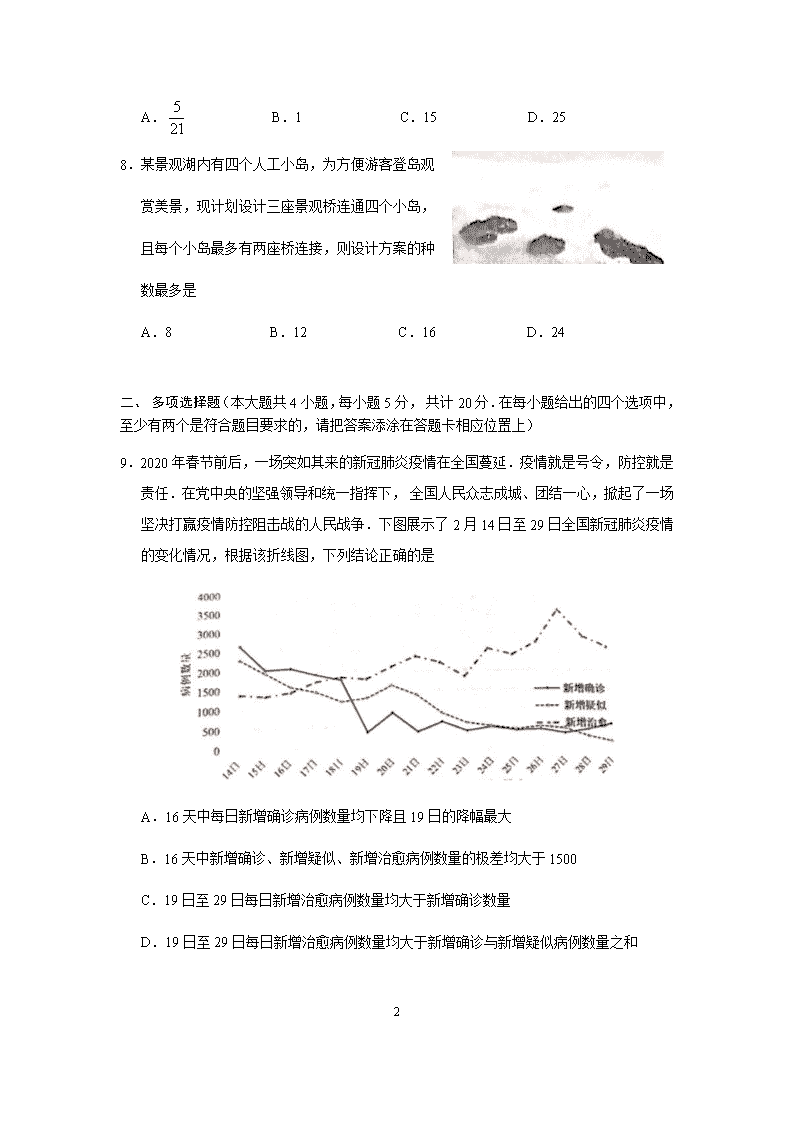
江苏省苏州市2019—2020学年下学期学业质量阳光指标调研卷 高一数学 2020.7 一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上) 1.下列导数运算正确的是 A.(C为常数) B. C.(e为自然对数的底数) D. 2.已知(i是虚数单位),则复数z的共轭复数= A.1﹣3i B.﹣1﹣3i C.﹣1+3i D.1+3i 3.函数图象的对称轴为直线x=1,则实数a= A.﹣1 B.0 C.1 D.1或﹣1 4.已知随机变量服从正太分布N(1,),若P(<4)=0.8,则P(﹣2<<1)= A.0.2 B.0.3 C.0.5 D.0.6 5.展开式中的常数项是 A.﹣270 B.﹣90 C.90 D.270 6.现有5个人独立地破译某个密码,已知每人单独译出密码的概率均为p,且<p<l,则恰有三个人译出密码的概率是 A. B. C. D. 7.若椭圆的一个焦点是(0,2),则实数k= 18 A. B.1 C.15 D.25 8.某景观湖内有四个人工小岛,为方便游客登岛观 赏美景,现计划设计三座景观桥连通四个小岛, 且每个小岛最多有两座桥连接,则设计方案的种 数最多是 A.8 B.12 C.16 D.24 二、 多项选择题(本大题共4小题,每小题5分, 共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上) 9.2020年春节前后,一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是号令,防控就是责任.在党中央的坚强领导和统一指挥下, 全国人民众志成城、团结一心,掀起了一场坚决打赢疫情防控阻击战的人民战争.下图展示了2月14日至29日全国新冠肺炎疫情的变化情况,根据该折线图,下列结论正确的是 A.16天中每日新增确诊病例数量均下降且19日的降幅最大 B.16 天中新增确诊、新增疑似、新增治愈病例数量的极差均大于1500 C.19日至29日每日新增治愈病例数量均大于新增确诊数量 D.19日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例数量之和 18 10.已知定义域为R的函数,且函数的图象如右图,则下列结论中正确的是 A. B.函数在区间(,﹣1)上单调递增 C.当x=1时,函数取得极小值 D.方程与均有三个实数根 11.如图,在正方体ABCD—A1B1C1D1中,P为线段BC1 上的一个动点,下列结论中正确的是 A.A1D⊥D1P B.平面PAD1⊥平面BCC1B1 C.存在唯一的点P,使得∠CPD1为90° D.当点P为BC1中点时,CP+PD1取得最小值 12.已知P是双曲线C:上任意一点,A,B是双曲线的两个顶点,设直线PA,PB的斜率分别为,(),若恒成立,且实数t的最大值为1,则下列说法正确的是 A.双曲线的方程为 B.双曲线的离心率为 C.函数(a>0,a≠1)的图象恒过双曲线C的一个焦点 D.直线x﹣y=0与双曲线C有两个交点 三、填空题(本大题共4小题, 每小题5分,共计20分.其中第16题共有2空, 18 第一个空2分,第二个空3分;其余题均为一空, 每空5分.请把答案填写在答题卡相应位置上) 13.不等式对任意x[4,16]恒成立,则实数a的取值范围为 . 14.如图,直线l是曲线在x=4处的切线,则= . 15.如图,将桌面上装有液体的圆柱形杯子倾斜角(母线与竖直方向所成角)后,液面呈椭圆形,当=30°时,该椭圆的离心率为 . 16.已知F为抛物线(p>1)的焦点,点A(1,p),M为抛物线上任意一点,的最小值为3,则p= ;若线段AF的垂直平分线交抛物线于P,Q两点,则四边形APFQ的面积为 .(本题第一空2分,第二空3分) 四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分) 解下列关于x的不等式: (1); (2). 18.(本小题满分12分) 已知函数(a≠1)为奇函数. (1)求实数a; (2)设函数.①求;②试证明函数 18 的图象关于点(0,1)对称. 19.(本小题满分12分) 如图,在四棱锥P—ABCD中,底面ABCD为正方形,PA=PD,且平面PAD⊥平面ABCD. (1)若E,F分别为棱PC,AB的中点,求证:CD⊥EF; (2)若直线PC与AB所成角的正弦值为,求二面角P—BC—A的余弦值. 18 20.(本小题满分12分) 苏州市从2020年6月1日起推进垃圾分类处理,是落实绿色发展理念的必然选择,也是打赢污染防治攻坚战的重要环节,为了解居民对垃圾分类的了解程度,某社区居委会随机抽取1000名社区居民参与问卷测试,并将问卷得分绘制频率分布表如下: 得分 [30,40) [40,50) [50,60) [60,70) [70,80) [80,90) [90,100] 男性人数 40 90 120 130 110 60 30 女性人数 20 50 80 110 100 40 20 (1)从该社区随机抽取一名居民参与问卷测试,试估计其得分不低于60分的概率; (2)将居民对垃圾分类的了解程度分为“比较了解”(得分不低于60分)和“不太了解”(得分低于60分)两类,完成2×2列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关? 不太了解 比较了解 总计 男性 女性 总计 (3)从参与问卷测试且得分不低于80分的居民中,按照性别进行分层抽样,共抽取10人,连同m (m)名男性调查员一起组成3个环保宜传组,若从这m+10人中随机抽取3人作为组长,且男性组长人数的期望不小于2,求m的最小值. 附公式及表如下:,其中. 18 P() 0.15 0.10 0.05 0.025 0.010 0.005 0.001 2.072 2.706 3.841 5.024 6.635 7.879 10.828 21.(本小题满分12分) 如图,已知椭圆E:(a>b>0)的右焦点为F(1,0),离心率e=,过F作一直线l1交椭圆E于A,B两点(其中A在x轴的上方),过点A作直线l2:x=4的垂线,垂足为C. (1)求椭圆E的方程; (2)问:在x轴上是否存在一个定点T,使得B,T,C三点共线?若存在,求出T的坐标;若不存在,请说明理由. 18 22.(本小题满分12分) 对于函数,,如果存在实数s,使得,同时成立,则称函数和互为“亲密函数”.若函数,(其中a,b,c,d为实数,e为自然对数的底数). (1)当a=0,b=﹣l,c=d=1时,判断函数和是否互为“亲密函数”,并说明理由; (2)当b=c=d=0时,若函数和互为“亲密函数”,求证:对任意的实数x都满足. 18 18 18 18 18 18 18 18 18 18 18查看更多