六年级数学下册教案-6 数学思考-人教版 (7)

六年级数学下册教案-6 数学思考-人教版 (7)

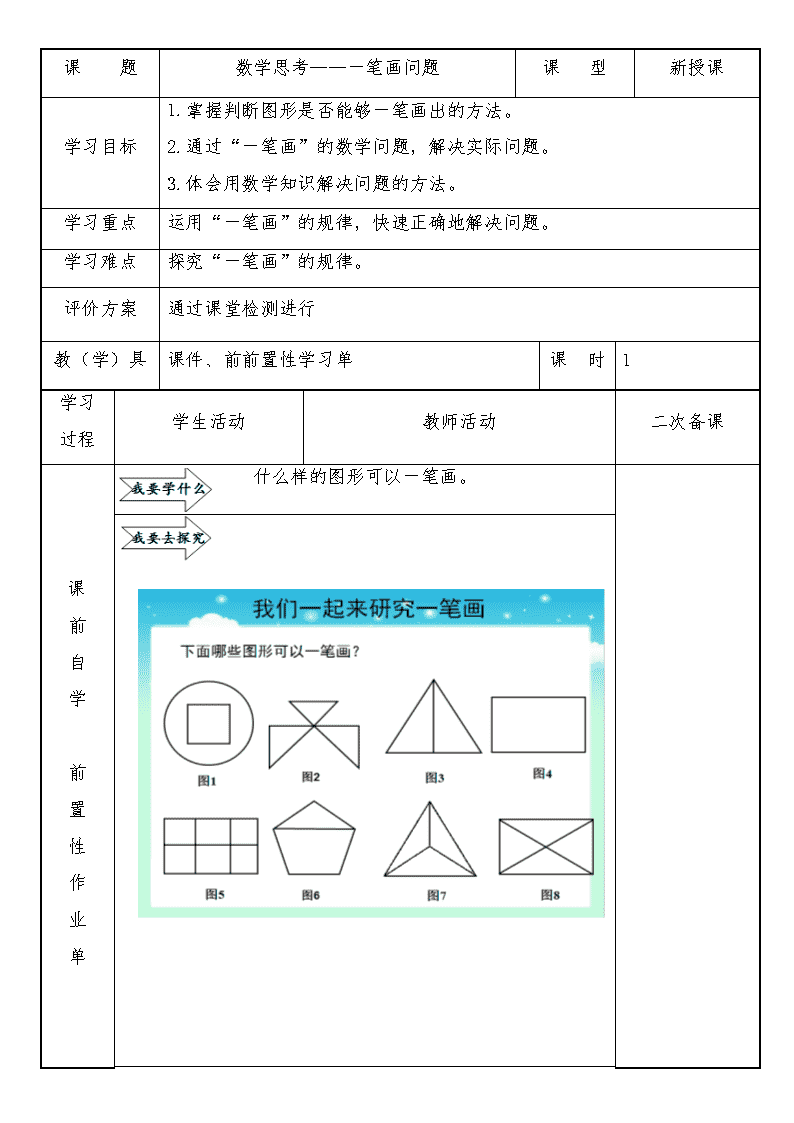
课 题 数学思考——一笔画问题 课 型 新授课 学习目标 1.掌握判断图形是否能够一笔画出的方法。 2.通过“一笔画”的数学问题，解决实际问题。 3.体会用数学知识解决问题的方法。 学习重点 运用“一笔画”的规律，快速正确地解决问题。 学习难点 探究“一笔画”的规律。 评价方案 通过课堂检测进行 教（学）具 课件、前前置性学习单 课 时 1 学习 过程 学生活动 教师活动 二次备课 课 前 自 学 前 置 性 作 业 单 什么样的图形可以一笔画。 课 中 研 学 找 1—3 名学生回 答。引导学生发现规 一、展示问题引入新课 18 世纪时风景秀丽的小城哥尼 斯堡中有一条河，河的中间有两个 小岛，河的两岸与两岛之间共建有 七座桥（如图），当时小城的居民中 流传着一道难题：一个人怎样才能 不重复地走过所有七座桥，再回到 出发点？ 这就是数学史上著名的七桥问 题，你愿意试一试吗？ 二、活动探究 一笔画的概念。（板书）从图形 上的某点出发，笔不离开纸，而且 每条线都只画一次，不准重复的画 完整幅图形。 师：小朋友看我们的学习单： 用笔沿着线条画一画，然后看哪些 能够一笔画出来，哪些不能，为什 通 过 故 事 的 形 式 把 问 题 引 出 来 ， 一 方 面 激 发 学 生 的 学 习 兴 趣 ， 另 一 方 面 也 可 以 让 学 生 感 受 到 他 们 今 天 探 讨 的 课 题 就 是 当 年 困 扰 千 百 人 的 问 题 ， 这 样 可 以 增 进 学 生 的 求 知 欲 。 接 着 让 学 生 通 过 对 七 座 桥 的 观 察 ， 在 图 上 试 走 等 活 动 ， 留 给 学 生 一 个 悬 念 ， 为 后 面 的 探 究 活 动 埋 下 伏 笔 ， 同 时 也 把 学 生 的 求 知 欲 望 推 上 了 一 个高潮。 律，一笔画是笔不离 开纸，那就是各部分 必须是连通的，（3） （4）不连通。 学生完成表格。 么？ 师：小朋友们不仅计算厉害， 图解能力也很强呀！老师非常高 兴，在图形中，我们把两条线想交 的位置称为点， 在一笔画中从一个点出发的线 的条数是奇数的点称为奇点。是偶 数的点是称为偶点。 师：小朋友们的学的很快，那 赶快来看看图中的点，标出每个点 各引出多少条线? 判断哪些可以一笔 画，哪些不能？ 师：请同学们完成学习单任务。 奇点个数 偶点个数 能否一笔画 尽量让学生自己总 结 。 学生尝试画七桥问题 的简图。 引导学生结合图表揭示规律： 1 没有奇点的连通图形是一笔 画，画时可以任一偶点为起点，最 后仍回到这个点。 2 只有两个奇点的连通图形是一 笔画，画时必须以一个奇点为起 点，以另一个奇点为终点。 3 奇点数超过两个的图形不是一 笔画。和偶点的数量没有关系 师 ： 同 学 们 今 天 表 现 特 别 优 秀，都学会了如何判断一笔画，还 记得我们上课之前的七桥问题吗？ 数学家欧拉知道了七桥问题，他用 四个点 A、B、C、D 分别表示小岛和 岸，用七条线段表示七座桥（如 图）于是问题就成为如何“一笔 画”出图中的图形。 三、课堂小节： 图 1 图 2 图 3 图 4 图 5 图 6 图 7 图 8 ● 点 A、B 表示 岛 点 C。D 表示岸 ▎线表示桥 同学们，今天学会了一笔画知识 后，就可以当未来的设计师了，把 我们的未来街道设计成能一笔画成 并且可以回到原点的路，把公园， 图书馆，超市等也设计成可以从某 点出发一笔画成的路线，不仅生活 便利，我们的城市也将更加美丽！ 课 尾 用 学 评 价 检 测 下图是一个公园的道路平面图，要使游客走遍每条路而又不 重复，出、人口应该设在哪 里？ 请你观察生活，设计一个运用“一笔画”的数学知识来解决 的实际问题。并与同伴交流。 板书 设计 主题：一笔画 一笔画的概念 各种图形 规律 课后 反思 《七桥问题与一笔画》是一个实验与探究的课题。这节课有两个重点：一是 实验，二是探究。所以在刚开始展示题目时，就让学生反复实验，最终仍是 不能一次不重复地走过七座桥。 接着是活动探究，这是本节课的首要重点。在充分理解教材的基础上，我创 造性地将教学内容重新打造，，特意为学生设计了一个探究的图形与表格，为 学生有效探究规律搭建了一个非常好的“手脚架”。学生在搜集、观察数据的 同时，引发对数学问题的思考，培养学生的观察能力，用表格、语言表示规 律，培养归纳猜想的能力。 其次，运用“一笔画”的规律解决七桥问题，并把七桥问题拓宽与深化。 最后，引出欧拉对七桥问题的建模，把实际问题转化成“一笔画”的数学问 题，并让学生体会到转化的数学思想以及从具体到抽象的思想。再次运用 “一笔画”的规律解决生活中的实际问题，把数学问题又转化并应用到实际 生活中，真正体现数学来源于生活并应用于生活这一特点，让学生感受到数 学的价值。