2008年中考数学分类真理练习11二次函数
二次函数
1、(2008庆阳)若,则由表格中信息可知与之间的函数关系式是( )
A. B.
图6
C. D.
答案:1、A
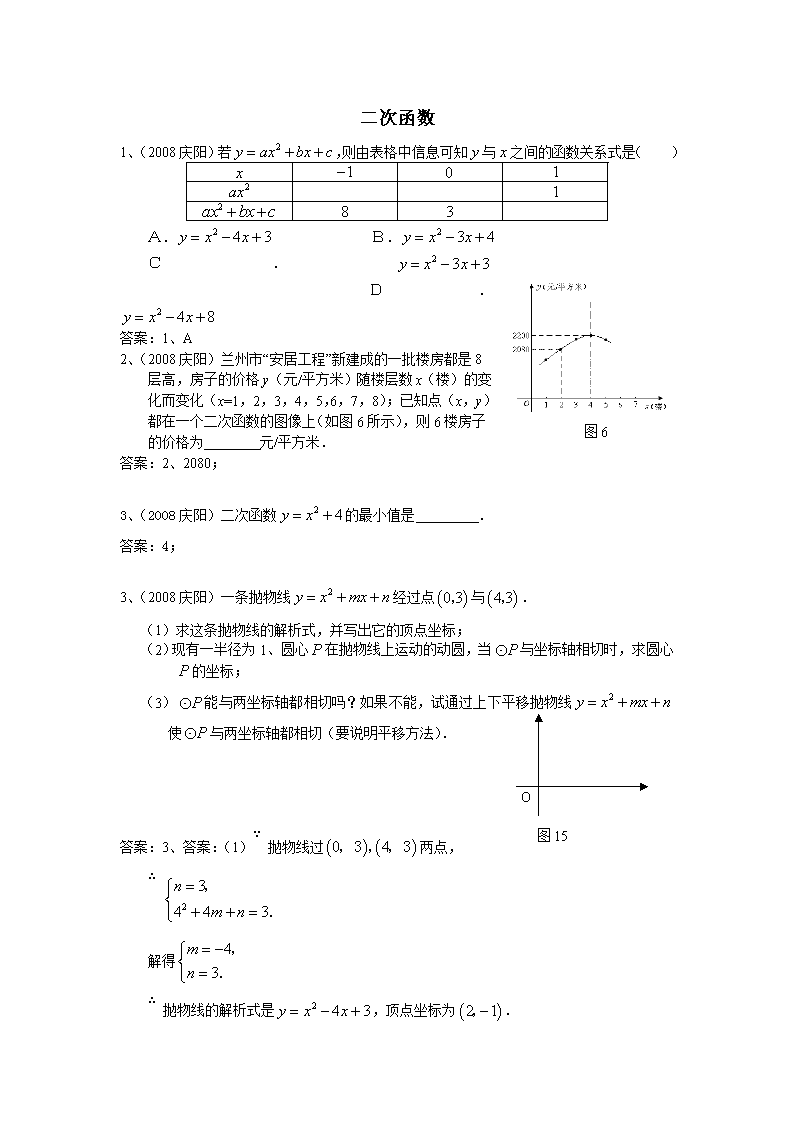
2、(2008庆阳)兰州市“安居工程”新建成的一批楼房都是8层高,房子的价格y(元/平方米)随楼层数x(楼)的变化而变化(x=1,2,3,4,5,6,7,8);已知点(x,y)都在一个二次函数的图像上(如图6所示),则6楼房子的价格为 元/平方米.
答案:2、2080;
3、(2008庆阳)二次函数的最小值是 .
答案:4;
3、(2008庆阳)一条抛物线经过点与.
(1)求这条抛物线的解析式,并写出它的顶点坐标;
(2)现有一半径为1、圆心在抛物线上运动的动圆,当与坐标轴相切时,求圆心的坐标;
O
图15
(3)能与两坐标轴都相切吗?如果不能,试通过上下平移抛物线使与两坐标轴都相切(要说明平移方法).
答案:3、答案:(1)∵ 抛物线过两点,
∴
解得
∴ 抛物线的解析式是,顶点坐标为.
(2)设点的坐标为,
当与轴相切时,有,∴.
由,得;
由,得.
此时,点的坐标为.
当与轴相切时,有,∴ .
由,得,解得;
由,得,解得.
此时,点的坐标为,.
综上所述,圆心的坐标为:,,.
注:不写最后一步不扣分.
(3) 由(2)知,不能.
设抛物线上下平移后的解析式为,
若能与两坐标轴都相切,则,
即x0=y0=1;或x0=y0=-1;或x0=1,y0=-1;或x0=-1,y0=1.
取x0=y0=1,代入,得h=1.
∴ 只需将向上平移1个单位,就可使与两坐标轴都相切.
4、(2008杭州)如图,记抛物线的图象与正半轴的交点为,将线段分成等份.设分点分别为,,,,过每个分点作轴的垂线,分别与抛物线交于点,,…,,再记直角三角形,,…的面积分别为,,…,这样就有,,…;记,当越来越大时,你猜想最接近的常数是( )
A. B. C. D.
答案:C;
5、(2008杭州)在直角坐标系中,设点,点.平移二次函数的图象,得到的抛物线满足两个条件:①顶点为;②与轴相交于两点().连接.
(1)是否存在这样的抛物线,使得?请你作出判断,并说明理由;
(第24题)
y
A
O
B
C
x
(2)如果,且,求抛物线对应的二次函数的解析式.
答案:
(1) ∵ 平移的图象得到的抛物线的顶点为,
∴ 抛物线对应的解析式为:. --- 2分
∵ 抛物线与x轴有两个交点,∴. --- 1分
令, 得,,
∴ )( )| ,
即, 所以当时, 存在抛物线使得.-- 2分
(2) ∵, ∴ , 得: ,
解得. --- 1分
在中,
1) 当时,由 , 得,
当时, 由, 解得,
此时, 二次函数解析式为; --- 2分
当时, 由, 解得,
此时,二次函数解析式为 + +. --- 2分
2) 当时, 由 , 将代, 可得, ,
(也可由代,代得到)
所以二次函数解析式为 + –或. --- 2分
(2008江西)11.将抛物线向上平移一个单位后,得到的抛物线解析式是 .
答案:
(2008江西)24.如图,抛物线相交于两点.
(1)求值;
(2)设与轴分别交于两点(点在点的左边),与轴分别交于两点(点在点的左边),观察四点的坐标,写出一条正确的结论,并通过计算说明;
y
x
P
A
O
B
B
(3)设两点的横坐标分别记为,若在轴上有一动点,且,过作一条垂直于轴的直线,与两条抛物线分别交于C,D两点,试问当为何值时,线段CD有最大值?其最大值为多少?
答案:解:(1)点在抛物线上,
, 2分
解得. 3分
(2)由(1)知,抛物线,. 5分
y
x
P
A
O
B
B
M
E
N
F
当时,解得,.
点在点的左边,,. 6分
当时,解得,.
点在点的左边,,. 7分
,,
点与点对称,点与点对称. 8分
y
x
P
A
O
B
D
Q
C
(3).
抛物线开口向下,抛物线开口向上. 9分
根据题意,得
. 11分
,当时,有最大值. 12分
说明:第(2)问中,结论写成“,四点横坐标的代数和为0”或“”均得1分.
(2008温州)5.抛物线的对称轴是( )
A.直线 B.直线 C.直线 D.直线
答案A
(2008温州)22.一次函数的图象与轴,轴分别交于点.一个二次函数的图象经过点.
(1)求点的坐标,并画出一次函数的图象;
(2)求二次函数的解析式及它的最小值.
答案(1)令,得,点的坐标是
令,得,点的坐标是
(2)二次函数的图象经过点,
,解得:.
二次函数的解析式是,
,函数的最小值为.
(2008金华)21.跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为y=ax2+bx+0.9.
(1)求该抛物线的解析式;
·
A
O
B
D
E
F
x
y
(2)如果小华站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶,请你算出小华的身高;
(3)如果身高为1.4米的小丽站在OD之间,且离
点O的距离为t米, 绳子甩到最高处时超过她的头
顶,请结合图像,写出t的取值范围 .
答案:(1)由题意得点E(1,1.4), B(6,0.9), 代入y=ax2+bx+0.9得
解得
∴所求的抛物线的解析式是y=-0.1x2+0.6x+0.9.
(2)把x=3代入y=-0.1x2+0.6x+0.9得 y=-0.1×32+0.6×3+0.9=1.8
∴小华的身高是1.8米
(3)1<t<5
1、(2008 嘉兴)一个函数的图象如图,给出以下结论:
①当时,函数值最大;
②当时,函数随的增大而减小;
③存在,当时,函数值为0.
其中正确的结论是( )
A.①② B.①③
C.②③ D.①②③
答案:C
2、(2008 绍兴)已知点,均在抛物线上,下列说法中正确的是( )答案:D
A.若,则 B.若,则
C.若,则 D.若,则
(2008甘肃白银)抛物线 y=x2+x-4与y轴的交点坐标为 .答案:(0,-4)
(2008甘肃白银)图20
如图20,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).
(1) 点A的坐标是__________,点C的坐标是__________;
(2) 当t= 秒或 秒时,MN=AC;
(3) 设△OMN的面积为S,求S与t的函数关系式;
(4) 探求(3)中得到的函数S有没有最大值?若有,求出最大值;
若没有,要说明理由.
解:(1)(4,0),(0,3);
(2) 2,6;
由△OMN∽△OAC,得,
∴ ON=,S=.
当4<t<8时,如图,∵ OD=t,∴ AD= t-4.
方法一:
由△DAM∽△AOC,可得AM=,∴ BM=6-.由△BMN∽△BAC,可得BN==8-t,∴ CN=t-4. S=矩形OABC的面积-Rt△OAM的面积- Rt△MBN的面积- Rt△NCO的面积=12--(8-t)(6-)-
=.
方法二:
易知四边形ADNC是平行四边形,∴ CN=AD=t-4,BN=8-t.由△BMN∽△BAC,可得BM==6-,∴ AM=.
以下同方法一.
(4) 有最大值.
方法一:
当0<t≤4时,∵ 抛物线S=的开口向上,在对称轴t=0的右边, S随t的增大而增大,∴ 当t=4时,S可取到最大值=6;当4<t<8时,
∵ 抛物线S=的开口向下,它的顶点是(4,6),∴ S<6.
综上,当t=4时,S有最大值6.
方法二:
∵ S=
-1
O
x=1
y
x
图5
∴ 当0<t<8时,画出S与t的函数关系图像,如图所示.
显然,当t=4时,S有最大值6.
(2008甘肃兰州)已知二次函数()的图象如图5所示,有下列4个结论:①;②;③;④;其中正确的结论有( B )
A.1个 B.2个 C.3个 D.4个
(2008甘肃兰州)下列表格是二次函数的自变量与函数值的对应值,判断方程(为常数)的一个解的范围是( C )
6.17
6.18
6.19
6.20
A. B.
C. D.
(2008甘肃兰州)2R米
30米
图11
在同一坐标平面内,下列4个函数①,②,③,④的图象不可能由函数的图象通过平移变换、轴对称变换得到的函数是 (填序号).答案:④
(2008甘肃兰州)农村常需要搭建截面为半圆形的全封闭蔬菜塑料暖房如图11所示,则需要塑
料布(m2)与半径(m)的函数关系式是(不考虑塑料埋在土里的部
分) .答案:
(2008甘肃兰州)一座拱桥的轮廓是抛物线型(如图16所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图17所示),求抛物线的解析式;
(2)求支柱的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.
y
x
O
B
A
C
图17
20m
10m
E
F
图16
6m
y
x
O
B
A
C
G
N
D
H
解:(1)根据题目条件,的坐标分别是.设抛物线的解析式为,将的坐标代入,得
解得.所以抛物线的表达式是.
(2)可设,于是
从而支柱的长度是米.
(3)设是隔离带的宽,是三辆车的宽度和,则点坐标是.过点作垂直交抛物线于,则.
根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.
11.二次函数
1.(2008齐齐哈尔T15).对于抛物线,下列说法正确的是( )
A.开口向下,顶点坐标 B.开口向上,顶点坐标
C.开口向下,顶点坐标 D.开口向上,顶点坐标
15.A
2. (2008哈尔滨市T21)21.小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x是多少时,矩形场地面积S最大?最大面积是多少?
(参考公式:二次函数y=ax2+bx+c=0,当x=时,)
21.解:(1)根据题意,得
自变量的取值范围是
(2),有最大值
当时,
答:当为15米时,才能使矩形场地面积最大,最大面积是225平方米.
1.(2008山东济南)(本小题满分9分)
已知:如图,直线与x轴相交于点A,与直线相交于点P.
(1)求点P的坐标.
(2)请判断的形状并说明理由.
F
第23题图
y
O
A
x
P
E
B
(3)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:① S与t之间的函数关系式.
② 当t为何值时,S最大,并求S的最大值.
.解:(1) 1分
解得: 2分
∴点P的坐标为(2,) 3分
F
第23题图1
y
O
A
x
P
E
B
D
(2)将代入
∴ ,即OA=4 4分
做PD⊥OA于D,则OD=2,PD=2
∵ tan∠POA=
∴ ∠POA=60° 5分
∵ OP=
∴△POA是等边三角形. 6分
(3)① 当0
2,∴当t=时,S最大= 9分
2.(2008山东济南).已知:抛物线(a≠0),顶点C (1,),与x轴交于A、B两点,.
(1)求这条抛物线的解析式.
(2)如图,以AB为直径作圆,与抛物线交于点D,与抛物线对称轴交于点E,依次连接A、D、B、E,点P为线段AB上一个动点(P与A、B两点不重合),过点P作PM⊥AE于M,PN⊥DB于N,请判断是否为定值? 若是,请求出此定值;若不是,请说明理由.
(3)在(2)的条件下,若点S是线段EP上一点,过点S作FG⊥EP ,FG分别与边AE、BE相交于点F、G(F与A、E不重合,G与E、B不重合),请判断是否成立.若成立,请给出证明;若不成立,请说明理由.
第24题图
C
O
x
A
D
P
M
E
B
N
y
解:(1)设抛物线的解析式为 1分
将A(-1,0)代入: ∴ 2分
∴ 抛物线的解析式为,即: 3分
(2)是定值, 4分
∵ AB为直径,∴ ∠AEB=90°,∵ PM⊥AE,∴ PM∥BE
∴ △APM∽△ABE,∴ ①
同理: ② 5分
① + ②: 6分
(3)∵ 直线EC为抛物线对称轴,∴ EC垂直平分AB
∴ EA=EB
∵ ∠AEB=90°
∴ △AEB为等腰直角三角形.
∴ ∠EAB=∠EBA=45° 7分
如图,过点P作PH⊥BE于H,
由已知及作法可知,四边形PHEM是矩形,
∴PH=ME且PH∥ME
在△APM和△PBH中
∵∠AMP=∠PHB=90°, ∠EAB=∠BPH=45°
∴ PH=BH
且△APM∽△PBH
∴
∴ ① 8分
在△MEP和△EGF中,
∵ PE⊥FG, ∴ ∠FGE+∠SEG=90°
∵∠MEP+∠SEG=90° ∴ ∠FGE=∠MEP
∵ ∠PME=∠FEG=90° ∴△MEP∽△EGF
∴ ②
由①、②知: 9分
(本题若按分类证明,只要合理,可给满分)
2、(2008 绍兴)定义为一次函数的特征数.
(1)若特征数是的一次函数为正比例函数,求的值;
(2)设点分别为抛物线与轴的交点,其中,且的面积为4,为原点,求图象过两点的一次函数的特征数.
解:(1)特征数为的一次函数为,
,
.
(2)抛物线与轴的交点为,
与轴的交点为.
若,则,;
若,则,.
当时,满足题设条件.
此时抛物线为.
它与轴的交点为,
与轴的交点为,
一次函数为或,
特征数为或.
(2008青海)10.二次函数图象如图所示,则点在第 象限.
答案:四
第10题图
O
x
y
(2008青海)28.王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间(单位:分钟)与学习收益量的关系如图甲所示,用于回顾反思的时间(单位:分钟)与学习收益量的关系如图乙所示(其中是抛物线的一部分,为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求王亮解题的学习收益量与用于解题的时间之间的函数关系式,并写出自变量的取值范围;
(2)求王亮回顾反思的学习收益量与用于回顾反思的时间之间的函数关系式;
(3)王亮如何分配解题和回顾反思的时间,才能使这30分钟的学习收益总量最大?
(学习收益总量解题的学习收益量回顾反思的学习收益量)
O
O
y
y
x
x
A
2
5
15
第28题图
图甲
图乙
4
25
答案:解:(1)设,
把代入,得.
. (1分)
自变量的取值范围是:. (2分)
(2)当时,
设, (3分)
把代入,得,.
. (5分)
当时,
(6分)
即.
(3)设王亮用于回顾反思的时间为分钟,学习效益总量为,
则他用于解题的时间为分钟.
当时,
. (7分)
当时,. (8分)
当时,
. (9分)
随的增大而减小,
当时,.
综合所述,当时,,此时. (10分)
即王亮用于解题的时间为26分钟,用于回顾反思的时间为4分钟时,学习收益总量最大.
(11分)
注:以上各题用不同于本参考答案的解法做正确的相应给分.
(2008赤峰)25.在平面直角坐标系中给定以下五个点.
(1)请从五点中任选三点,求一条以平行于轴的直线为对称轴的抛物线的解析式;
(2)求该抛物线的顶点坐标和对称轴,并画出草图;
y
O
x
G
F
H
(3)已知点在抛物线的对称轴上,直线过点且垂直于对称轴.验证:以为圆心,为半径的圆与直线相切.请你进一步验证,以抛物线上的点为圆心为半径的圆也与直线
相切.由此你能猜想到怎样的结论.
解:(1)设抛物线的解析式为,
且过点,
由在H .
则. (2分)
y
O
x
F
H
Q
M
N
得方程组,
解得.
抛物线的解析式为 (4分)
(2)由 (6分)
得顶点坐标为,对称轴为. (8分)
(3)①连结,过点作直线的垂线,垂足为,
则.
在中,,,
,
,
以点为圆心,为半径的与直线相切. (10分)
②连结过点作直线的垂线,垂足为.过点作垂足为,
则.
在中,,.
.
以点为圆心为半径的与直线相切. (12分)
③以抛物线上任意一点为圆心,以为半径的圆与直线相切. (14分)
(2008宁夏)23.已知二次函数.
(1) 求此二次函数的图象与轴的交点坐标.
(2)二次函数的图象如图所示,将的图象经过怎样的平移,就可以得到二次函数的图象.
(参考:二次函数图象的顶点坐标是())
解:(1) 解得 ,
∴图象与轴的交点坐标为(,0)和(,0) 4分
(2)
∴顶点坐标为(,)
将二次函数图象向右平移1个单位,再向下平移2个单位,就可得到二次函数的图象
(2008年江苏省无锡市,26T,9分)已知抛物线与它的对称轴相交于点,与轴交于,与轴正半轴交于.
(1)求这条抛物线的函数关系式;
(2)设直线交轴于是线段上一动点(点异于),过作轴交直线于,过作轴于,求当四边形的面积等于时点的坐标.
26.解:(1)由题意,知点是抛物线的顶点,
(2分)
,,抛物线的函数关系式为. (3分)
(2)由(1)知,点的坐标是.设直线的函数关系式为,
则,,. (4分)
由,得,,点的坐标是.
设直线的函数关系式是,
则解得,.
直线的函数关系式是. (5分)
设点坐标为,则.
轴,点的纵坐标也是.
设点坐标为,
点在直线上,,. (6分)
轴,点的坐标为,
,,,
, (7分)
,,,当时,,
而,,
点坐标为和. (9分)
(2008年江苏省南通市,24T,8分)已知点A(-2,-c)向右平移8个单位得到点A′,A与A′两点均在抛物线上,且这条抛物线与y轴的交点的纵坐标为-6,求这条抛物线的顶点坐标.
24.解:由抛物线与y轴交点的纵坐标为-6,得c=-6.
∴A(-2,6),点A向右平移8个单位得到点A′(6,6)
∵A与A′两点均在抛物线上,
∴,解这个方程组,得
故抛物线的解析式是
∴抛物线顶点坐标为(2,-10)
(2008江苏省无锡) 已知抛物线与它的对称轴相交于点,与轴交于,与轴正半轴交于.
(1)求这条抛物线的函数关系式;
(2)设直线交轴于是线段上一动点(点异于),过作轴交直线于,过作轴于,求当四边形的面积等于时点的坐标.
解:(1)由题意,知点是抛物线的顶点,
(2分)
,,抛物线的函数关系式为. (3分)
(2)由(1)知,点的坐标是.设直线的函数关系式为,
则,,. (4分)
由,得,,点的坐标是.
设直线的函数关系式是,
则解得,.
直线的函数关系式是. (5分)
设点坐标为,则.
轴,点的纵坐标也是.
设点坐标为,
点在直线上,,. (6分)
轴,点的坐标为,
,,,
, (7分)
,,,当时,,
而,,
点坐标为和. (9分)
(2008江苏省宿迁)在平面直角坐标系中,函数与的图象大致是
答案选D
(2008江苏省宿迁)某宾馆有客房间,当每间客房的定价为每天元时,客房会全部住满.当每间客房每天的定价每涨元时,就会有间客房空闲.如果旅客居住客房,宾馆需对每间客房每天支出元的各种费用.
(1)请写出该宾馆每天的利润(元)与每间客房涨价(元)之间的函数关系式;
(2)设某天的利润为元,元的利润是否为该天的最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时客房定价应为多少元?
(3)请回答客房定价在什么范围内宾馆就可获得利润?
解:(1)由题意得即.
(2) 元的利润不是为该天的最大利润.
∵
∴当即每间客房定价为元时,宾馆当天的最大利润为元.
(3)由得,即
解得,由题意可知当客房的定价为:大于元而小于元时,宾馆就可获得利润.
(2008江苏省宿迁)如图,⊙的半径为,正方形顶点坐标为,顶点在⊙上运动.
(1)当点运动到与点、在同一条直线上时,试证明直线与⊙相切;
(2)当直线与⊙相切时,求所在直线对应的函数关系式;
(3)设点的横坐标为,正方形的面积为,求与之间的函数关系式,并求出的最大值与最小值.
第27题
解:(1) ∵四边形为正方形 ∴
∵、、在同一条直线上 ∴ ∴直线与⊙相切;
第27题图1
(2)直线与⊙相切分两种情况:
①如图1, 设点在第二象限时,过作轴于点,设此时的正方形的边长为,则,解得或(舍去).
由∽ 得
第27题图2
∴ ∴,故直线的函数关系式为;
②如图2, 设点在第四象限时,过作轴于点,设此时的正方形的边长为,则,解得或(舍去).
由∽ 得
∴ ∴,故直线的函数关系式为.
(3)设,则,由得
∴
∵
∴.
x
y
O
3
-1
第14题图
14.(2008安徽)如图为二次函数的图象,在下列说法中:
①;②方程的根为,;
③;④当时,随着的增大而增大.
正确的说法有 .(请写出所有正确说法的序号)
答案①②④
21.(2008安徽)杂技团进行杂技表演,演员从跷跷板右端处弹跳到人梯顶端椅子
处,其身体(看成一点)的路线是抛物线的一部分,如图.
(1)求演员弹跳离地面的最大高度;
[解] .
,函数的最大值是.
答:演员弹跳的最大高度是米.
(2)已知人梯高米,在一次表演中,人梯到起跳点的水平距离是4米,问这次表演是否成功?请说明理由.
[解]
x(米)
y(米)
B
C
O
第21题图
当时,,所以这次表演成功.
9.(2008芜湖)函数在同一直角坐标系内的图象大致是 ( )
答案C
24.(2008芜湖)(本小题满分15分)
如图,已知 ,,现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
(1) 求C点坐标及直线BC的解析式;
(2) 一抛物线经过B、C两点,且顶点落在x轴正半轴上,求该抛物线的解析式并画出函数图象;
(3) 现将直线BC绕B点旋转与抛物线相交与另一点P
,请找出抛物线上所有满足到直线AB距离为的点P.
解:
(1)
过C点向x轴作垂线,垂足为D,由位似图形性质可知:
△ABO∽△ACD, ∴.
由已知,可知: .
∴.∴C点坐标为.
直线BC的解析是为:
化简得:
(2)设抛物线解析式为,由题意得: ,
解得:
∴解得抛物线解析式为或.
又∵的顶点在x轴负半轴上,不合题意,故舍去.
∴满足条件的抛物线解析式为
(准确画出函数图象)
(3) 将直线BC绕B点旋转与抛物线相交与另一点P,设P到 直线AB的距离为h,
故P点应在与直线AB平行,且相距的上下两条平行直线和上.
由平行线的性质可得:两条平行直线与y轴的交点到直线BC的距离也为.
如图,设与y轴交于E点,过E作EF⊥BC于F点,
在Rt△BEF中,,
∴.∴可以求得直线与y轴交点坐标为
同理可求得直线与y轴交点坐标为
∴两直线解析式;.
根据题意列出方程组: ⑴;⑵
∴解得:;;;
∴满足条件的点P有四个,它们分别是,,,
[注:对于以上各大题的不同解法,解答正确可参照评分!]
26.(08南京)(8分)已知二次函数中,函数与自变量的部分对应值如下表:
…
…
…
…
(1)求该二次函数的关系式;
(2)当为何值时,有最小值,最小值是多少?
(3)若,两点都在该函数的图象上,试比较与的大小.
解:(1)根据题意,当时,;当时,.
所以
解得
所以,该二次函数关系式为. 2分
(2)因为,
所以当时,有最小值,最小值是1. 4分
(3)因为,两点都在函数的图象上,
所以,,.
. 5分
所以,当,即时,;
当,即时,;
当,即时,. 8分
19.(08连云港)(本小题满分8分)
如图,在平面直角坐标系中,点的坐标分别为.
(1)请在图中画出,使得与关于点成中心对称;
(2)若一个二次函数的图象经过(1)中的三个顶点,求此二次函数的关系式.
x
O
y
A
C
B
P
(第19图)
解:(1)如图所示. 3分
x
O
y
A
C
B
P
(第19答图)
(2)由(1)知,点的坐标分别为.
由二次函数图象与轴的交点的坐标为,
故可设所求二次函数关系式为. 5分
将的坐标代入,得,解得.
故所求二次函数关系式为. 8分
24.(08连云港)(本小题满分14分)
如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的,处,直角边在轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至处时,设与分别交于点,与轴分别交于点.
(1)求直线所对应的函数关系式;
(2)当点是线段(端点除外)上的动点时,试探究:
①点到轴的距离与线段的长是否总相等?请说明理由;
A
O
E
G
B
F
H
N
C
P
I
x
y
M
(第24题图)
D
II
②两块纸板重叠部分(图中的阴影部分)的面积是否存在最大值?若存在,求出这个最大值及取最大值时点的坐标;若不存在,请说明理由.
解:(1)由直角三角形纸板的两直角边的长为1和2,
知两点的坐标分别为.
设直线所对应的函数关系式为. 2分
有解得
A
O
E
G
B
F
H
N
C
P
I
x
y
M
(第24题答图)
K
II
所以,直线所对应的函数关系式为. 4分
(2)①点到轴距离与线段的长总相等.
因为点的坐标为,
所以,直线所对应的函数关系式为.
又因为点在直线上,
所以可设点的坐标为.
过点作轴的垂线,设垂足为点,则有.
因为点在直线上,所以有. 6分
因为纸板为平行移动,故有,即.
又,所以.
法一:故,
从而有.
得,.
所以.
又有. 8分
所以,得,而,
从而总有. 10分
法二:故,可得.
故.
所以.
故点坐标为.
设直线所对应的函数关系式为,
则有解得
所以,直线所对的函数关系式为. 8分
将点的坐标代入,可得.解得.
而,从而总有. 10分
②由①知,点的坐标为,点的坐标为.
. 12分
当时,有最大值,最大值为.
取最大值时点的坐标为. 14分
[2008福建省南平市]25.(14分)如图,平面直角坐标系中有一矩形纸片,为原点,点分别在轴,轴上,点坐标为(其中),在边上选取适当的点和点,将沿翻折,得到;再将沿翻折,恰好使点与点重合,得到,且.
(1)求的值;
(2)求过点的抛物线的解析式和对称轴;
(3)在抛物线的对称轴上是否存在点,使得是等腰三角形?若不存在,请说明理由;若存在,直接答出所有满足条件的点的坐标(不要求写出求解过程).
【提示:抛物线的对称轴是,顶点坐标是】
25.(1)解法一:,
由题意可知,, 2分
, 3分
.又, 4分
解法二:,
由题意可知,, 2分
, 3分
4分
(2)解法一:过作直线轴于,
则,,故. 5分
又由(1)知,
设过三点的抛物线解析式为
抛物线过原点,. 6分
又抛物线过两点, 解得
所求抛物线为 8分
它的对称轴为. 9分
解法二:过作直线轴于,
则,,故. 5分
又由(1)知,点关于直线对称,点为抛物线的顶点 6分
于是可设过三点的抛物线解析式为
抛物线过点,,解得
所求抛物线为 8分
它的对称轴为. 9分
(3)答:存在 10分
满足条件的点有,,,.(每空1分) 14分
[2008年福建省宁德市]26.(本题满分14分)如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
⑴求y1与x的函数关系,并在图2中画出y1的图象;
⑵如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
⑶在图2中,点G是x轴正半轴上一点(0<OG<6=,过G作EF垂直于x轴,分别交y1、y2于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
图2
G
2 4 6 8 10
1210
8
6
4
2
y
O
x
解:
图1
C Q→ B
D
A
P↓
26.解:⑴∵,CD=3,CQ=x,
E
G
2 4 6 8 10
1210
8
6
4
2
y
O
x
F
∴.
图象如图所示.
⑵方法一:,CP=8k-xk,CQ=x,
∴.
∵抛物线顶点坐标是(4,12),
∴.
解得.
则点P的速度每秒厘米,AC=12厘米.
方法二:观察图象知,当x=4时,△PCQ面积为12.
此时PC=AC-AP=8k-4k=4k,CQ=4.
∴由,得 .解得.
则点P的速度每秒厘米,AC=12厘米.
方法三:设y2的图象所在抛物线的解析式是.
∵图象过(0,0),(4,12),(8,0),
∴ 解得
∴. ①
∵,CP=8k-xk,CQ=x,
∴. ②
比较①②得.
则点P的速度每秒厘米,AC=12厘米.
⑶①观察图象,知
线段的长EF=y2-y1,表示△PCQ与△DCQ的面积差(或△PDQ面积).
②由⑵得 .(方法二,)
∵EF=y2-y1,
∴EF=,
∵二次项系数小于0,
∴在范围,当时,最大.
(2008苏州)初三数学课本上,用“描点法”画二次函数的图象时,列了如下表格:
…
0
1
2
…
…
…
根据表格上的信息回答问题:该二次函数在时, —4 .
(2008徐州)已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5)
①求该函数的关系式;
②求该函数图象与坐标轴的交点坐标;
③将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,
求△O A′B′的面积.
答案:(1) (2)(0,3),(-3,0),(1,0) (3)略
(2008苏州)如图,抛物线与轴的交点为.直线与
轴交于,与轴交于.若两点在直线上,且,.为线段的中点,为斜边上的高.
(1)的长度等于 ; , .
(2)是否存在实数,使得抛物线上有一点,满足以为顶点的三角形与相似?
D
(第29题)
x
y
N
O
M
P
A
C
B
H
若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的点(简要说明理由);并进一步探索对符合条件的每一个点,直线与直线的交点是否总满足,写出探索过程.
解:(1);,.
(2)设存在实数,使抛物线上有一点,满足以为顶点的三角形与等腰直角相似.
以为顶点的三角形为等腰直角三角形,且这样的三角形最多只有两类,一类是以为直角边的等腰直角三角形,另一类是以为斜边的等腰直角三角形.
①若为等腰直角三角形的直角边,则.
由抛物线得:,.
,.的坐标为.
D
(第29题)
x
y
N
O
M
P
A
C
B
H
把代入抛物线解析式,得.
抛物线解析式为.
即.
②若为等腰直角三角形的斜边,
则,.
的坐标为.
把代入抛物线解析式,得.
抛物线解析式为,即
当时,在抛物线上存在一点满足条件,如果此抛物线上还有满足条件的点,不妨设为点,那么只有可能是以为斜边的等腰直角三角形,由此得,显然不在抛物线上,因此抛物线上没有符合条件的其他的点.
当时,同理可得抛物线上没有符合条件的其他的点.
当的坐标为,对应的抛物线解析式为时,
和都是等腰直角三角形,.
又,.
,,总满足.
当的坐标为,对应的抛物线解析式为时,
同理可证得:,总满足.
(2008 沈阳市)7.二次函数的图象的顶点坐标是( )
A. B. C. D.
答案:A
(2008 沈阳市)26.如图所示,在平面直角坐标系中,矩形的边在轴的负半轴上,边在轴的正半轴上,且,,矩形绕点按顺时针方向旋转后得到矩形.点的对应点为点,点的对应点为点,点的对应点为点,抛物线过点.
(1)判断点是否在轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在轴的上方是否存在点,点,使以点为顶点的平行四边形的面积是矩形面积的2倍,且点在抛物线上,若存在,请求出点,点的坐标;若不存在,请说明理由.
y
x
O
第26题图
D
E
C
F
A
B
答案:解:(1)点在轴上 1分
理由如下:
连接,如图所示,在中,,,
,
由题意可知:
点在轴上,点在轴上. 3分
(2)过点作轴于点
,
在中,,
点在第一象限,
点的坐标为 5分
由(1)知,点在轴的正半轴上
点的坐标为
点的坐标为 6分
抛物线经过点,
由题意,将,代入中得
解得
所求抛物线表达式为: 9分
(3)存在符合条件的点,点. 10分
理由如下:矩形的面积
以为顶点的平行四边形面积为.
由题意可知为此平行四边形一边,
又
边上的高为2 11分
依题意设点的坐标为
点在抛物线上
解得,,
,
以为顶点的四边形是平行四边形,
y
x
O
D
E
C
F
A
B
M
,,
当点的坐标为时,
点的坐标分别为,;
当点的坐标为时,
点的坐标分别为,.
(2008 大连市)21.如图10,直线和抛物线都经过点A(1,0),B(3,2).
⑴求m的值和抛物线的解析式;
⑵求不等式的解集(直接写出答案).
答案:
解:(1)∵直线y=x+m经过点A(1,0) ………………………………………………1分
∴0=1+m………………………………………………2分
∴m=-1.即m的值为-1………………………………………………3分
∵抛物线y=x+bx+c经过点A(1,0),B(3,2). ………………………………………………4分
∴………………………………………………6分
解得………………………………………………7分
∴二次函数的解析式为y=.………………………………………………8分
(2008 大连市)26.如图18,点C、B分别为抛物线C1:,抛物线C2:的顶点.分别过点B、C作x轴的平行线,交抛物线C1、C2于点A、D,且AB = BD.
⑴求点A的坐标;
⑵如图19,若将抛物线C1:“”改为抛物线
“”.其他条件不变,求CD的长和的值.
附加题:如图19,若将抛物线C1:“”改为抛物线
“”,其他条件不变,求的值.
答案:
解:(1)如图9,连结AC、BC,直线AB交y轴于点E.
∵AB∥x轴,CD∥x轴,C、B为抛物线的顶点,
∴AC=CB,BC=BD. ∵AB=BD,
∴AC=BC=AB. ………………………………………………1分
∴∠ACE=30°.设AE=m,∴CE=m.
∵,∴点C的坐标为(0,1).
∴点A的坐标为(-m,1+m).………………………………………………2分
∵点A在抛物线上,
∴1+m=m+1,
∴.
∴点A的坐标为(-,4). ………………………………………………3分
(2)如图10,过点C作CE⊥AB于E.
设抛物线,
∴点C的坐标为.
设AE=m,∴CE=.
∴点A的坐标为.………………………………………………4分
∵点A在抛物线上,
∴=.
解得 ………………………………………………5分
由(1)同理可得,CD=BD=BC=AB. ………………………………………………6分
∵AB=2AE=, ………………………………………………7分
∴CD=,即CD的长为.
由题意得,点B的坐标为().
又∵点B是抛物线C 的顶点,
∴y=(x-.………………………………………………8分
∵抛物线C经过点C,
∴k=(h-.………………………………………………9分
∴=-2,即的值为-2.………………………………………………10分
附加题:
解:如图10,设.
∴点C的坐标为.
过点C作CE⊥AB于E,设AE=m,则CE=.
∴点B的坐标为.………………………………………1分
∵点B在抛物线C上,∴=.
∵m≠0,∴m=.
∴点B的坐标为().
∵点B是抛物线C 的顶点,∴y=(x-.
∵抛物线C经过点C,
∴k=(h-.
∴=-a,………………………………………………2分
∴y=-a(x-.
=-a[]+.……………………3分
∴. ………………………………………4分
∴.∴.
∴.即的值为.……………………………5分
9.(08荆门)把抛物线y=x2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=x2-3x+5,则( )A
(A)b=3,c=7. (B)b=6,c=3. (C)b=-9,c=-5. (D)b=-9,c=21.
27.(08荆门) (10分)某人定制了一批地砖,每块砖是边长为0.4m的正方形ABCD,如图19(1),点E、F分别在边BC、CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD这三种材料的每平方米价格依次为30元、20元、10元.这将此种地砖按图19(2)所示的形式铺设,且能使中间的阴影部分组成四边形EFGH.
(1)判断图19(2)中四边形EFGH是何形状,说明理由;
(2)E、F在什么位置时,定制这批地砖所需材料费用最省?
(1) (2)
图19
解:(1) 四边形EFGH是正方形. ……………………………………………2分
图(2)可以看作是由四块图(1)所示地砖绕C点按顺(逆)时针方向旋转90°后得到的,故CE=CF =CG.∴△CEF是等腰直角三角形.因此四边形EFGH是正方形. 4分
(2)设CE=x,则BE=0.4-x,每块地砖的费用为y,那么
y=x×30+×0.4×(0.4-x)×20+[0.16-x-×0.4×(0.4-x)×10]
=10(x-0.2x+0.24)
=10[(x-0.1)2+0.23](0<x<0.4). ………………………………………8分
当x=0.1时,y有最小值,即费用为最省,此时CE=CF=0.1.
答:当CE=CF=0.1米时,总费用最省. ………………………………………10分
28.(08荆门) (12分)如图20,已知抛物线y=ax2+bx+c的顶点A在x轴上,与y轴的交点为B(0,1),且b=-4ac.
(1)求抛物线的解析式.
(2)在抛物线上是否存在一点C,使以BC为直径的圆经过抛物线的顶点A?若不存在,说明理由;若存在,求出点C的坐标,并求出此时圆的圆心点P的坐标.
(3)根据(2)小题的结论,你发现B、P、C三点横坐标、纵坐标之间分别有何关系?
图20
第28题图
O
x
y
A
C
B
P
P1
D
P2
P
(1)由抛物线过B(0,1)得c=1.
又b=-4ac, 顶点A(-,0),
∴-==2c=2.∴A(2,0). ………………………………………2分
将A点坐标代入抛物线解析式,得4a+2b+1=0,
∴ 解得a =,b =-1.
故抛物线的解析式为y=x2-x+1. ………………………………………4分
另解:由抛物线过B(0,1)得c=1.又b2-4ac=0,b=-4ac,∴b=-1. ……2分
∴a=,故y=x-x+1. ……………………………………………4分
(2)假设符合题意的点C存在,其坐标为C(x,y),作CD⊥x轴于D ,连接AB、AC.∵A在以BC为直径的圆上,∴∠BAC=90°.∴ △AOB∽△CDA.∴OB·CD=OA·AD.
1·y=2(x-2), ∴y=2x-4. ……………………6分
由 解得x1=10,x2=2.
∴符合题意的点C存在,且坐标为 (10,16),或(2,0).………………………8分
∵P为圆心,∴P为BC中点.
当点C坐标为(10,16)时,取OD中点P1,连PP1,则PP1为梯形OBCD中位线.
∴PP1=(OB+CD)=.∵D (10,0),∴P1 (5,0),∴P (5,).
当点C坐标为(2,0)时,取OA中点P2 ,连PP2 ,则PP2为△OAB的中位线.
∴PP2=OB=.∵A(2,0),∴P2(1,0),∴P(1,).
故点P坐标为(5,),或(1,). ………………………………………10分
(3)设B、P、C三点的坐标为B(x1,y1),P(x2,y2),C(x3,y3),由(2)可知:
………………………………………12分
9.(08泰州)二次函数的图像可以由二次函数的图像平移而得到,下列平移正确的是( )B
A.先向左平移2个单位长度,再向上平移1个单位长度
B.先向左平移2个单位长度,再向下平移1个单位长度
C.先向右平移2个单位长度,再向上平移1个单位长度
D.先向右平移2个单位长度,再向下平移1个单位长度
29.(08泰州)已知二次函数的图像经过三点,,.
(1)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像;(5分)
(2)若反比例函数()的图像与二次函数()的图像在第一象限内交于点,落在两个相邻的正整数之间.请你观察图像,写出这两个相邻的正整数;(4分)
(3)若反比例函数()的图像与二次函数()的图像在第一象限内的交点为,点的横坐标满足,试求实数的取值范围.(5分)
y
x
1
O
2
3
4
4
3
2
1
第29题图
(1)设抛物线解析式为y=a(x-1)(x+3) ………………………………………1分
(只要设出解析式正确,不管是什么形式给1分)
将(0,)代入,解得.
∴抛物线解析式为 ……………………………………………3分
(无论解析式是什么形式只要正确都得分)
画图(略).(没有列表不扣分)……………………………………………………5分
(2)正确的画出反比例函数在第一象限内的图像 …………………………………7分
由图像可知,交点的横坐标x0落在1和2之间,从而得出这两个相邻的正整
数为1与2. ………………………………………………………………………9分
(3)由函数图像或函数性质可知:当2<x<3时,
对y1=,y1随着x的增大而增大,对y2=(k>0),
y2随着x的增大而减小.因为A(x0,y0)为二次函数图像与反比例函数图像的交点,
所以当x0=2时,由反比例函数图象在二次函数上方得y2>y1.即>,
解得k>5. …………………………………………………………………………11分
同理,当x0=3时,由二次函数数图象在反比例函上方得y1>y2,
即>,解得k<18. …………………………………………13分
所以k的取值范围为5<k<18. ………………………………………………14分
1、(3T)(2008湖北省黄冈市,3分)抛物线的对称轴为直线 .
2、(14T)( 2008湖北省襄樊,3分)如图7,一名男生推铅球,铅球行进高度(单位:m)与水平距离(单位:m)之间的关系是.则他将铅球推出的距离是
m.10
3、(19T)(2008湖北省黄冈市,本题满分8分)四川汶川大地震发生后,我市某工厂车间接到生产一批帐篷的紧急任务,要求必须在12天(含12天)内完成.已知每顶帐篷的成本价为800元,该车间平时每天能生产帐篷20顶.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高.这样,第一天生产了22顶,以后每天生产的帐篷都比前一天多2顶.由于机器损耗等原因,当每天生产的帐篷数达到30顶后,每增加1顶帐篷,当天生产的所有帐篷,平均每顶的成本就增加20元.设生产这批帐篷的时间为天,每天生产的帐篷为顶.
(1)直接写出与之间的函数关系式,并写出自变量的取值范围.
(2)若这批帐篷的订购价格为每顶1200元,该车间决定把获得最高利润的那一天的全部利润捐献给灾区.设该车间每天的利润为元,试求出与之间的函数关系式,并求出该车间捐款给灾区多少钱?
4、(25T)( 2008湖北省襄樊,本小题满分12分)
如图15,四边形是矩形,,,将矩形沿直线折叠,使点落在处,交于.
(1)求的长;
(2)求过三点抛物线的解析式;
(3)若为过三点抛物线的顶点,一动点从点出发,沿射线以每秒1个单位长度的速度匀速运动,当运动时间(秒)为何值时,直线把分成面积之比为的两部分?
25.解:(1)四边形是矩形,
,.
又,.
.
,
即,
解之,得.
(2).如图4,过作于,
.
,.,.
.
因点为坐标原点,故可设过三点抛物线的解析式为.
解之,得
.
(3)抛物线的对称轴为,其顶点坐标为.
设直线的解析式为,则解之,得
.
设直线交直线于,过作于.
..
或,
或,或.
或,即或.
,.
直线的解析式为.当时,.
直线的解析式为.当时,.
当秒或秒时,直线把分成面积之比为的两部分.
5、(20T)(2008湖北省黄冈市,本题满分14分)已知:如图,在直角梯形中,,以为原点建立平面直角坐标系,三点的坐标分别为,点为线段的中点,动点从点出发,以每秒1个单位的速度,沿折线的路线移动,移动的时间为秒.
(1)求直线的解析式;
(2)若动点在线段上移动,当为何值时,四边形的面积是梯形面积的?
(3)动点从点出发,沿折线的路线移动过程中,设的面积为,请直接写出与的函数关系式,并指出自变量的取值范围;
(4)当动点在线段上移动时,能否在线段上找到一点,使四边形
为矩形?请求出此时动点的坐标;若不能,请说明理由.
A
B
D
C
O
x
y
(此题备用)
A
B
D
C
O
P
x
y
2.(2008内江市)如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
2米
(2题图)
1米
2.5米
0.5米
答案:0.5
9.(2008资阳市)在平面直角坐标系中,如果抛物线y=2x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是
A.y=2(x-2)2 + 2 B.y=2(x + 2)2-2
图3
C.y=2(x-2)2-2 D.y=2(x + 2)2 + 2
答案:B
24.(2008资阳市)(本小题满分12分)
如图10,已知点A的坐标是(-1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求抛物线的解析式;
图10
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.
(1) ∵以AB为直径作⊙O′,交y轴的负半轴于点C,
∴∠OCA+∠OCB=90°,
又∵∠OCB+∠OBC=90°,
∴∠OCA=∠OBC,
又∵∠AOC= ∠COB=90°,
∴ΔAOC∽ ΔCOB, 1分
∴.
又∵A(–1,0),B(9,0),
∴,解得OC=3(负值舍去).
∴C(0,–3),
3分
设抛物线解析式为y=a(x+1)(x–9),
∴–3=a(0+1)(0–9),解得a=,
∴二次函数的解析式为y=(x+1)(x–9),即y=x2–x–3. 4分
(2) ∵AB为O′的直径,且A(–1,0),B(9,0),
∴OO′=4,O′(4,0), 5分
∵点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,
∴∠BCD=∠BCE=×90°=45°,
连结O′D交BC于点M,则∠BO′D=2∠BCD=2×45°=90°,OO′=4,O′D=AB=5.
∴D(4,–5). 6分
∴设直线BD的解析式为y=kx+b(k≠0)
∴ 7分
图10答案图1
解得
∴直线BD的解析式为y=x–9. 8分
(3) 假设在抛物线上存在点P,使得∠PDB=∠CBD,
解法一:设射线DP交⊙O′于点Q,则.
分两种情况(如答案图1所示):
①∵O′(4,0),D(4,–5),B(9,0),C(0,–3).
∴把点C、D绕点O′逆时针旋转90°,使点D与点B重合,则点C与点Q1重合,
因此,点Q1(7,–4)符合,
∵D(4,–5),Q1(7,–4),
∴用待定系数法可求出直线DQ1解析式为y=x–. 9分
解方程组得
∴点P1坐标为(,),[坐标为(,
)不符合题意,舍去].
10分
②∵Q1(7,–4),
∴点Q1关于x轴对称的点的坐标为Q2(7,4)也符合.
∵D(4,–5),Q2(7,4).
∴用待定系数法可求出直线DQ2解析式为y=3x–17. 11分
解方程组得
∴点P2坐标为(14,25),[坐标为(3,–8)不符合题意,舍去].
12分
∴符合条件的点P有两个:P1(,),P2(14,25).
图10答案图2
解法二:分两种情况(如答案图2所示):
①当DP1∥CB时,能使∠PDB=∠CBD.
∵B(9,0),C(0,–3).
∴用待定系数法可求出直线BC解析式为y=x–3.
又∵DP1∥CB,∴设直线DP1的解析式为y=x+n.
把D(4,–5)代入可求n= –,
∴直线DP1解析式为y=x–. 9分
1. (2008黄石)若实数满足,则的最小值是 .
答案:2
2. (2008黄石)某公司有型产品40件,型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型利润
型利润
甲店
200
170
乙店
160
150
(1)设分配给甲店型产品件,这家公司卖出这100件产品的总利润为(元),求关于的函数关系式,并求出的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店型产品让利销售,每件让利元,但让利后型产品的每件利润仍高于甲店型产品的每件利润.甲店的型产品以及乙店的型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
答案:依题意,甲店型产品有件,乙店型有件,型有件,则
(1)
.
由解得. (2分)
(2)由,
.
,,39,40.
有三种不同的分配方案.
①时,甲店型38件,型32件,乙店型2件,型28件.
②时,甲店型39件,型31件,乙店型1件,型29件.
③时,甲店型40件,型30件,乙店型0件,型30件.
(3)依题意:
.
①当时,,即甲店型40件,型30件,乙店型0件,型30件,能使总利润达到最大.
②当时,,符合题意的各种方案,使总利润都一样.
③当时,,即甲店型10件,型60件,乙店型30件,型0件,能使总利润达到最大. (8分)
1. (2008黄石)如图,已知抛物线与轴交于点,,与轴交于点.
(1)求抛物线的解析式及其顶点的坐标;
(2)设直线交轴于点.在线段的垂直平分线上是否存在点,使得点到直线的距离等于点到原点的距离?如果存在,求出点的坐标;如果不存在,请说明理由;
(3)过点作轴的垂线,交直线于点,将抛物线沿其对称轴平移,使抛物线与线段总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
A
B
C
O
x
y
答案:
(1)设抛物线解析式为,把代入得.
,
顶点 (2分)
(2)假设满足条件的点存在,依题意设,
由求得直线的解析式为,
它与轴的夹角为,设的中垂线交于,则.
则,点到的距离为.
又. (4分)
.
平方并整理得:
.
存在满足条件的点,的坐标为. (6分)
(3)由上求得.
A
B
C
O
x
y
D
F
H
P
E
①若抛物线向上平移,可设解析式为.
当时,.
当时,.
或.
. (8分)
②若抛物线向下移,可设解析式为.
由,
有.
,.
向上最多可平移72个单位长,向下最多可平移个单位长. (10分)
(滨州市2008)11、若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是( )
A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y1<y3<y2
答案:B
(济宁市2008)11.已知二次函数的图象如图所示,则这个二次函数的表达式为( )
A. B.
C. D.
答案:B
(滨州市2008)24.(本题满分12分)
如图(1),已知在中,AB=AC=10,AD为底边BC上的高,且AD=6。将沿箭头所示的方向平移,得到。如图(2),交AB于E,分别交AB、AD于G、F。以为直径作,设的长为x,的面积为y。
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连结EF,求EF与相切时x的值;
(3)设四边形的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?
答案:
24.
(2008深圳)1、将二次函数的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是
A. B.
C. D.
答案:A
(2008福州市)
10.(2008福州市) 已知抛物线与轴的一个交点为,则代数式的值为( )
A.2006 B.2007 C.2008 D.2009
答案D
22.(2008福州市) (本题满分14分)
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(第22题)
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
答案 解:(1);.
(2)在中,,
.
设点的坐标为,其中,
顶点,
设抛物线解析式为.
①如图①,当时,,
.
解得(舍去);.
.
.
解得.
抛物线的解析式为
②如图②,当时,,
.
解得(舍去).
③当时,,这种情况不存在.
综上所述,符合条件的抛物线解析式是.
(3)存在点,使得四边形的周长最小.
如图③,作点关于轴的对称点,作点关于轴的对称点,连接,分别与轴、轴交于点,则点就是所求点.
,.
.
.
又,
,此时四边形的周长最小值是.
(第15题图)
(2008龙岩市)
15.已知函数的图象如图所示,
则下列结论正确的是( )
A.a>0,c>0 B.a<0,c<0
C.a<0,c>0 D.a>0,c<0
答案D
(2008年贵阳市)8.二次函数的最小值是(B )
A. B. C. D.
(2008年贵阳市)9.对任意实数,点一定不在( C )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(2008年贵阳市)25.(本题满分12分)
某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加元.求:
(1)房间每天的入住量(间)关于(元)的函数关系式.(3分)
(2)该宾馆每天的房间收费(元)关于(元)的函数关系式.(3分)
(3)该宾馆客房部每天的利润(元)关于(元)的函数关系式;当每个房间的定价为每天多少元时,有最大值?最大值是多少?(6分)
解:(1). 3分
(2) 3分
(3) 2分
4分
当时,有最大值.
此时,,就是说,当每个房间的定价为每天410元时,有最大值,且最大值是15210元. 6分
(2008 河南)14、如图是二次函数图像的一部分,该图在轴右侧与轴交点的坐标是
答案:(1,0)
(2008 河南)23、(本题满分11分)
如图,抛物线与轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当=O和=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
(1)求这条抛物线的解析式;
(2)P为线段OM上一点,过点P作PQ⊥轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
(3)随着点P的运动,四边形PQCO的面积S有最大值吗?如果S有最大值,请求出S的最大值并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;
(4)随着点P的运动,是否存在t的某个值,能满足PO=OC?如果存在,请求出t的值。
答案:(本小题满分11分)
解:(1)∵当和时,的值相等,∴,……1分
∴,∴
将代入,得,
将代入,得………………………………………….2分
∴设抛物线的解析式为
将点代入,得,解得.
∴抛物线,即……………………………..3分
(2)设直线OM的解析式为,将点M代入,得,
∴……………………………………………………………………..4分
则点P,,而,.
=.......................5分
的取值范围为:<≤.......................................6分
(3)随着点的运动,四边形的面积有最大值.
从图像可看出,随着点由→运动,的面积与的面积在不断增大,即不断变大,显当然点运动到点时,最值...............7分
此时时,点在线段的中点上............. ................8分
因而.
当时,,∥,∴四边形是平行四边形. ..9分
(4)随着点的运动,存在,能满足.................10分
设点,,. 由勾股定理,得.
∵,∴,<,(不合题意)
∴当时,...................................11分
(2008 鸡西)15.对于抛物线,下列说法正确的是( )
A.开口向下,顶点坐标 B.开口向上,顶点坐标
C.开口向下,顶点坐标 D.开口向上,顶点坐标
答案:A
(2008湖北宜昌23).如图,在Rt△ABC中,AB=AC,P是边AB(含端点)上的动点.过P作BC的垂线PR,R为垂足,∠PRB的平分线与AB相交于点S,在线段RS上存在一点T,若以线段PT为一边作正方形PTEF,其顶点E,F恰好分别在边BC,AC上.
(1)△ABC与△SBR是否相似,说明理由;
(2)请你探索线段TS与PA的长度之间的关系;
(第23题)
(3)设边AB=1,当P在边AB(含端点)上运动时,请你探索正方形PTEF的面积y的最小值和最大值.
解:(1)(第23题图1)
∵RS是直角∠PRB的平分线,∴∠PRS=∠BRS=45°.
在△ABC与△SBR中,∠C=∠BRS=45°,∠B是公共角,
∴△ABC∽△SBR...(1分)
(2)线段TS的长度与PA相等.(2分)
∵四边形PTEF是正方形,
∴PF=PT,∠SPT+∠FPA=180°-∠TPF=90°,
在Rt△PFA中,∠PFA +∠FPA=90°,
∴∠PFA=∠TPS,
∴Rt△PAF≌Rt△TSP,∴PA=TS.(3分)
当点P运动到使得T与R重合时,
这时△PFA与△TSP都是等腰直角三角形且底边相等,即有PA=TS.
(第23题图2)
(第23题图3)
(若下面解题中没有求出x的取值范围是0≤x≤,
以上的讨论可评1分)
由以上可知,线段ST的长度与PA相等.
(3)由题意,RS是等腰Rt△PRB的底边PB上的高,
∴PS=BS, ∴BS+PS+PA=1, ∴PS=.(4分)
设PA的长为x,易知AF=PS,
则y=PF=PA+PS,得y=x+(),
即y=,(5分)
根据二次函数的性质,当x=时,y有最小值为.(6分)
如图2,当点P运动使得T与R重合时,PA=TS为最大.
易证等腰Rt△PAF≌等腰Rt△PSR≌等腰Rt△BSR,
∴PA=
如图3,当P与A重合时,得x=0.
∴x的取值范围是0≤x≤.(7分) (此处为独立得分点,只要求出x≤即可得1分)
∴①当x的值由0增大到时,y的值由减小到(8分)
∴②当x的值由增大到时,y的值由增大到.(8分)
(说明:①②任做对一处评1分,两处全对也只评一分)
∵≤≤,∴在点P的运动过程中,
正方形PTEF面积y的最小值是,y的最大值是.(9分)
(2008湖北宜昌24).用煤燃烧发电时,所说的标准煤是指含热量为7 000大卡/千克的煤.生产实际中,一般根据含热量相等,把所需标准煤的用煤量折合成含相同热量的实际用煤量来计算.(“大卡/千克”为一种热值单位)
光明电厂生产中每发一度电需用标准煤0.36千克,现有煤矸石和大同煤两种可选为生产实际用煤,这两种煤的基本情况见下表:
煤的
品种
含热量
(大卡/千克)
只用本种煤每发一度电的用煤量
(千克/度)
平均每燃烧一吨煤发电的生产成本
购煤费用
(元/吨)
其他费用
(元/吨)
煤矸石
1 000
2.52
150
a(a>0)
大同煤
6 000
m
600
a2
(1)求生产中只用大同煤每发一度电的用煤量(即表中m的值);
(2)根据环保要求,光明电厂在大同煤中掺混煤矸石形成含热量为5 000大卡/千克的混合煤来燃烧发电,若使用这种混合煤比全部使用大同煤每发1 000度电的生产成本增加了5.04元,求表中a的值.(生产成本=购煤费用+其它费用)
解:(1)光明电厂生产1度电所用的大同煤为m千克,而标准煤用量为0.36千克,
由题意,得0.36×7 000=m×6 000,解得 m=0.42(2分)
(或6 000 m=1 000×2.52)
煤的
品种
含热量
(大卡/千克)
只用本种煤每发一度电的用煤量
(千克/度)
平均每燃烧一吨煤发电的生产成本
购煤费用
(元/吨)
其他费用
(元/吨)
煤矸石
1 000
2.52
150
a (a>0)
大同煤
6 000
0.42
600
a2
混合煤
5 000
0.504
510
0.8a2+0.2 a
(2)设1吨含热量为5000大卡/千克的混合煤中含p吨大同煤和q吨煤矸石.
则 ,解得,(3分)
(计算出混合煤中大同煤占80%,煤矸石占20%,或比例为4:1,即评1分)
故购买1吨混合煤费用为0.8×600+0.2×150=510(元),
其他费用为0.8a+0.2 a2 元. (4分)
设光明电厂生产1度电用的混合煤为h千克,
则, 解得h=0.504(千克). (5分)
[或:设生产1千度电用的混合煤中含x吨大同煤和y吨煤矸石.
则 ,解得,(5分)]
生产1千度电用的大同煤:1 000×0.42=420 (千克)=0.42(吨),
生产1千度电用的混合煤:1 000×0.504=504(千克)=0.504(吨),
由题意可知数量关系:
5.04=平均每燃烧1吨混合煤发电的生产成本×生产1千度电所用混合煤
-平均每燃烧1吨大同煤发电的生产成本×生产1千度电所用大同煤 (※6分)
即:(510+0.8a2+0.2 a)×0.504-(600+a2)×0.42=5.04 (8分)
(所列方程正确,※未叙述仍评8分)
化简并整理,得 0.1008 a—0.0168 a2=0. (9分)
(也可以直接写出方程:
)
解得 a1=6, a2=0,(不合题意,应舍去)
所以表中a的值为6. (10分)
(2008湖北宜昌25).如图1,已知四边形OABC中的三个顶点坐标为O(0,0),A(0,n),C(m,0).动点P从点O出发依次沿线段OA,AB,BC向点C移动,设移动路程为z,△OPC的面积S随着z的变化而变化的图象如图2所示.m,n是常数, m>1,n>0.
(1)请你确定n的值和点B的坐标;
(图1) (图2)
(第25题)
(2)当动点P是经过点O,C的抛物线y=ax+bx+c的顶点,且在双曲线y=上时,求这时四边形OABC的面积.
.解:(1) 从图中可知,当P从O向A运动时,△POC的面积S=mz, z由0逐步增大到2,则S由0逐步增大到m,故OA=2,n=2 . (1分)
同理,AB=1,故点B的坐标是(1,2).(2分)
(2)解法一:
∵抛物线y=ax+bx+c经过点O(0,0),C(m ,0),∴c=0,b=-am,(3分)
∴抛物线为y=ax-amx,顶点坐标为(,-am2).(4分)
(25题图1)
如图1,设经过点O,C,P的抛物线为l.
当P在OA上运动时,O,P都在y轴上,
这时P,O,C三点不可能同在一条抛物线上,
∴这时抛物线l不存在, 故不存在m的值..①
当点P与C重合时,双曲线y=不可能经过P,
故也不存在m的值.②(5分)
(说明:①②任做对一处评1分,两处全对也只评一分)
当P在AB上运动时,即当02,与 x=≤1不合,舍去.(6分)③
容易求得直线BC的解析式是:,(7分)
当P在BC上运动,设P的坐标为 (x,y),当P是顶点时 x=,
故得y==,顶点P为(,),
∵1< x=2,又∵P在双曲线y=上,
于是,×=,化简后得5m-22m+22=0,
解得,,(8分)
与题意2
查看更多