北师大版初中数学矩形、正方形教案

北师大版初中数学矩形、正方形教案

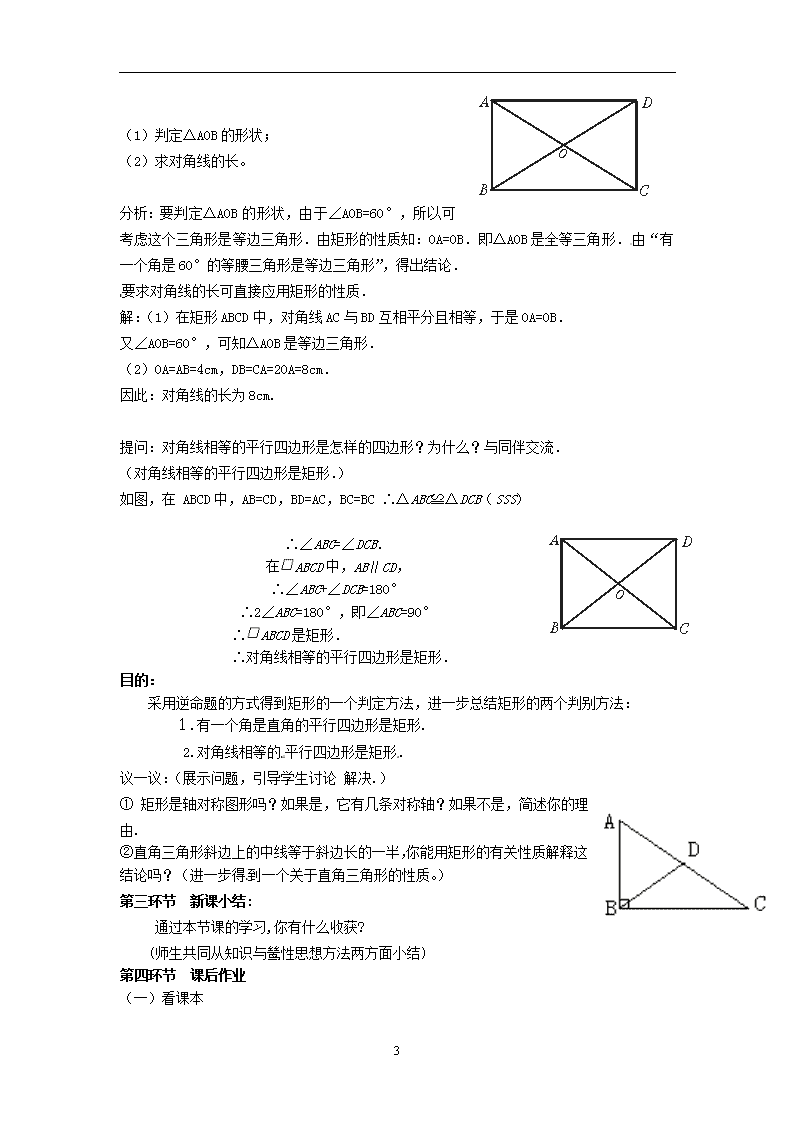
‎ ‎ ‎4.4矩形、正方形（一）‎ 一、学生起点分析 学生已经学习了平行四边形的性质和判定，也学习了一种特殊的平行四边形——菱形的性质和判定，对于类似的问题有一定的学习精力、经验和感受，这将更有利于学生对本节课的学习。‎ 二、教学任务分析 教学目标：‎ ‎ 知识目标 ‎1．掌握矩形的概念、性质和判别条件.‎ ‎2．提高对矩形的性质和判别在实际生活中的应用能力.‎ 能力目标 经历探索矩形的性质和判别条件的过程，在直观操作活动和简单的说理过程中发展合情推理能力，主观探索习惯，逐步掌握说理的基本方法.‎ 情感与价值观 在操作活动过程中，加深对矩形的的认识，以此激发学生的探索精神。‎ 教学重点：本节课的重点是矩形的性质和常用判别方法的理解和掌握。‎ 教学难点：本节课的难点是矩形的性质和常用判别方法的综合应用。‎ 三、教学过程 课前准备：‎ 教具准备：像框；用四根木条制作一个平行四边形教具．‎ 学生用具：皮筋，活动的平行四边形框架．‎ 教学过程设计分成四分环节：‎ 第一环节：巧设情境问题，引入课题 第二环节：讲授新课 第三环节：新课小结 第四环节：布置作业 第一环节　巧设情境问题，引入课题 ‎ 给出活动的平行四边形教具，请学生观察当它的一个内角由锐角变为钝角的过程中，会形成怎样的特殊图形情况．（进行演示，如图）进而引入本节课的主题——矩形。（当然这一过程，也可以通过计算机演示）‎ 第二环节　讲授新课 ‎ 主要环节：‎ ‎（1）根据演示过程，请学生尝试给矩形下定义。‎ ‎（2）寻找生活中的矩形。‎ 4‎ ‎ ‎ ‎（3）探索矩形的性质。‎ ‎（4）通过练习，加强学生对矩形性质的理解。‎ ‎（5）矩形的判定。‎ ‎（6）从对称的角度再认识矩形。‎ 目的：‎ 1． 矩形是学生比较熟悉的图形，小学甚至更早学生就已经接触到。但是当时对于矩形的理解和认识是停留在表象层面的，即提到矩形，学生往往联想到的是具体的图形和形象，不能离开实物去研究图形。随着学生的思维水平的提高，这里采取的动画的方式，请学生给矩形下定义，就是要让学生在直观从把握矩形的本质特征，从而将对矩形的理解上升到形式化的高度。‎ 2． 对矩形性质的探索，采用了类比的方式，在平行四边形性质的基础上加强条件。在讨论的过程中，进一步得到了直角三角形的一个性质（斜边上的中线等于斜边的一半）‎ 3． 通过将性质“反过来”的方法（逆命题），得到矩形的判定条件。‎ 第（3）－（6）的主要过程：‎ 拿出准备好的平行四边形活动框架，来做一做：‎ 在一个平行四边形活动框架上，用两根像皮筋分别套在相对的两个顶点上，拉动一对不相邻的顶点，改变平行四边形的形状：‎ ‎ ‎ ‎ ‎ ‎（1）随着∠α的变化，两条对角线的长度分别是怎样变化的？‎ ‎（2）当∠α是锐角时，两条对角线的长度有什么关系？当∠α是钝角时呢？‎ ‎（3）当∠α是直角时，平行四边形变成矩形，此时两条对角线的长度有什么关系？‎ ‎（学生进行活动，探索矩形的性质）‎ 当∠α是锐角或钝角时，两条对角线是不相等的．‎ 当∠α是直角时，平行四边形变为矩形，这时两条对角线的长度相等．‎ 归纳矩形的性质：（引导学生归纳，并体会矩形的“对称美”.）‎ 1． 矩形的对边平行且相等； ‎ 2． 矩形的四个角都是直角；‎ 3． 矩形的对角线相等且互相平分；‎ 4． 矩形是轴对称图形.‎ ‎［例1］如图在矩形ABCD中，两条对角线AC，BD相交于点O，∠AOB=60°，AB=4 cm．‎ 4‎ ‎ ‎ ‎ ‎ ‎（1）判定△AOB的形状；‎ ‎（2）求对角线的长。‎ 分析：要判定△AOB的形状，由于∠AOB=60°，所以可考虑这个三角形是等边三角形．由矩形的性质知：OA=OB．即△AOB是全等三角形．由“有一个角是60°的等腰三角形是等边三角形”，得出结论．‎ 要求对角线的长可直接应用矩形的性质．‎ 解：（1）在矩形ABCD中，对角线AC与BD互相平分且相等，于是OA=OB．‎ 又∠AOB=60°，可知△AOB是等边三角形．‎ ‎（2）OA=AB=4cm，DB=CA=2OA=8cm．‎ 因此：对角线的长为8cm.‎ 提问：对角线相等的平行四边形是怎样的四边形？为什么？与同伴交流．‎ ‎（对角线相等的平行四边形是矩形．）‎ 如图，在 ABCD中，AB=CD，BD=AC，BC=BC ∴△ABC≌△DCB（SSS） ‎ ‎∴∠ABC=∠DCB．‎ 在ABCD中，AB∥CD，‎ ‎∴∠ABC+∠DCB=180°‎ ‎∴2∠ABC=180°，即∠ABC=90°‎ ‎∴ABCD是矩形．‎ ‎∴对角线相等的平行四边形是矩形．‎ 目的：‎ 采用逆命题的方式得到矩形的一个判定方法，进一步总结矩形的两个判别方法：‎ ‎　　　　１.有一个角是直角的平行四边形是矩形.‎ ‎ 2.对角线相等的平行四边形是矩形. ‎ 议一议：（展示问题，引导学生讨论 解决.）‎ ‎① 矩形是轴对称图形吗？如果是，它有几条对称轴？如果不是，简述你的理由.‎ ‎② 直角三角形斜边上的中线等于斜边长的一半，你能用矩形的有关性质解释这结论吗？（进一步得到一个关于直角三角形的性质。）‎ 第三环节　新课小结:‎ ‎ 通过本节课的学习,你有什么收获?‎ ‎(师生共同从知识与鸶性思想方法两方面小结)‎ 第四环节　课后作业 ‎（一）看课本 4‎ ‎ ‎ ‎（二）课本习题4.6　‎ 四、教学设计反思 ‎ 矩形和菱形一样都是在平行四边形的基础上，强化条件得到的。两者的地位是一样的，前者强化了角的条件，后者强化了边的条件。因此这两节课在处理方式上，在教学过程中，可以采取类似的方法。通过这种类似的方法，也让学生感受到数学上解决问题的常用的方式：可以通过类比，可以通过在类比的基础上强化条件等手段得到猜测。‎ 4‎