2015年数学理高考课件5-3 等比数列及其前n项和

2015年数学理高考课件5-3 等比数列及其前n项和

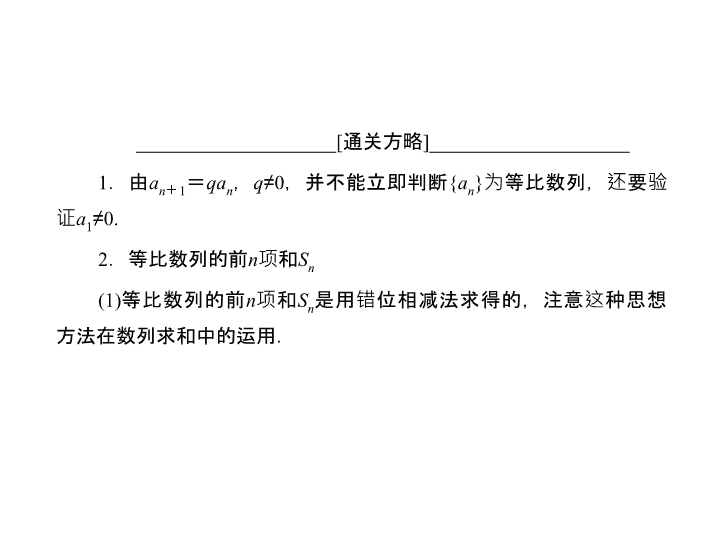
[ 最新考纲展示 ] 　 1 ． 理解等比数列的概念．　 2. 掌握等比数列的通项公式与前 n 项和公式．　 3. 能在具体的问题情境中识别数列的等比关系，并能用有关知识解决相应的问题．　 4. 了解等比数列与指数函数的关系． 第三节　等比数列及其前 n 项和 等比数列的相关概念 ____________________[ 通关方略 ]____________________ 1 ．由 a n ＋ 1 ＝ qa n ， q ≠ 0 ，并不能立即判断 { a n } 为等比数列，还要验证 a 1 ≠ 0. 2 ．等比数列的前 n 项和 S n (1) 等比数列的前 n 项和 S n 是用错位相减法求得的，注意这种思想方法在数列求和中的运用． 1 ．已知 { a n } 为等比数列， a 4 ＋ a 7 ＝ 2 ， a 5 a 6 ＝－ 8 ，则 a 1 ＋ a 10 ＝ ( 　　 ) A ． 7 　　　　 B ． 5 　　　　 C ．－ 5 　　　　 D ．－ 7 答案： D 答案 ： 2 n 3 ．设公比为 q ( q >0) 的等比数列 { a n } 的前 n 项和为 S n . 若 S 2 ＝ 3 a 2 ＋ 2 ， S 4 ＝ 3 a 4 ＋ 2 ，则 q ＝ ________. 等比数列的性质 设数列 { a n } 是等比数列， S n 是其前 n 项和． (1) 若 m ＋ n ＝ p ＋ q ，则 ，其中 m ， n ， p ， q ∈ N * . 特别地，若 2 s ＝ p ＋ r ，则 a p a r ＝ ，其中 p ， s ， r ∈ N * . (2) 相隔等距离的项组成的数列仍是等比数列，即 a k ， a k ＋ m ， a k ＋ 2 m ， … 仍是等比数列，公比为 ( k ， m ∈ N * ) ． a m a n ＝ a p a q q m 等比 (4) S m ＋ n ＝ S n ＋ S m ＝ S m ＋ S n . (5) 当 q ≠ － 1 ，或 q ＝－ 1 且 k 为 数时， S k ， S 2 k － S k ， S 3 k － S 2 k ， … 是等比数列． q n q m 奇 等比 q q ____________________[ 通关方略 ]____________________ 1 ．在性质 (5) 中，当 q ＝－ 1 且 k 为偶数时， S k ， S 2 k － S k ， S 3 k － S 2 k ， … 不是等比数列； 2 ．在运用等比数列及其前 n 项和的性质时，要注意字母间的上标、下标的对应关系． 答案： B 5 ．已知 { a n } 为等比数列， a 4 ＝ 4 ，则 a 2 a 6 等于 ( 　　 ) A ． 4 B ． 8 C ． 16 D ． 32 答案： C 等比数列的判定 注： ① 前两种方法是判定等比数列的常用方法，而后两种方法常用于选择、填空中的判定． ② 若要判定一个数列不是等比数列，则只需判定其任意的连续三项不成等比即可． 等比数列的基本运算 [ 答案 ] 　 (1)A 　 (2)C 反思总结 1 ． 等比数列基本量的运算是等比数列中的一类基本问题，数列中有五个量 a 1 ， n ， q ， a n ， S n ，一般可以 “ 知三求二 ” ，通过列方程 ( 组 ) 可迎刃而解． 2 ．解决此类问题的关键是熟练掌握等比数列的有关公式，并灵活运用，在运算过程中，还应善于运用整体代换思想简化运算的过程． 等比数列的性质 [ 答案 ] 　 12 反思总结 在应用相应性质解题时，要注意性质成立的前提条件，有时需要进行适当变形．此外，解题时注意设而不求思想的运用． 变式训练 2 ．设各项都是正数的等比数列 { a n } ， S n 为前 n 项和，且 S 10 ＝ 10 ， S 30 ＝ 70 ，那么 S 40 ＝ ( 　　 ) A ． 150 B ．－ 200 C ． 150 或－ 200 D ． 400 或－ 50 解析： 依题意，数列 S 10 ， S 20 － S 10 ， S 30 － S 20 ， S 40 － S 30 成等比数列，因此有 ( S 20 － S 10 ) 2 ＝ S 10 ( S 30 － S 20 ) ，即 ( S 20 － 10) 2 ＝ 10(70 － S 20 ) ，故 S 20 ＝－ 20 或 S 20 ＝ 30 ；又 S 20 >0 ，因此， S 20 ＝ 30 ， S 20 － S 10 ＝ 20 ， S 40 ＝ 10 ＋ 20 ＋ 40 ＋ 80 ＝ 150 ，选 A. 答案： A —— 分类讨论思想在等比数列中的应用 分类讨论思想在等比数列中应用较多，常见的分类讨论有： (1) 已知 S n 与 a n 的关系，要分 n ＝ 1 ， n ≥ 2 两种情况． (2) 等比数列中遇到求和问题要分公比 q ＝ 1 ， q ≠ 1 讨论． (3) 项数的奇、偶数讨论． (4) 等比数列的单调性的判断注意与 a 1 ， q 的取值的讨论． 由题悟道 本题关键是在错位相减求和时出现 S n 的系数为 1 － p 2 . 此时应判断 1 － p 2 是否为零，从而分 p ＝ 1 ， p ＝－ 1 ， p ≠ ±1 三种情况讨论． 设等比数列 { a n } 的公比为 q ，前 n 项和 S n >0( n ＝ 1,2,3 ， … ) ．则 q 的取值范围为 ________ ． 答案： ( － 1,0)∪(0 ，＋∞ ) 本小节结束 请按 ESC 键返回