2015年数学理高考课件5-5 数列的综合应用

2015年数学理高考课件5-5 数列的综合应用

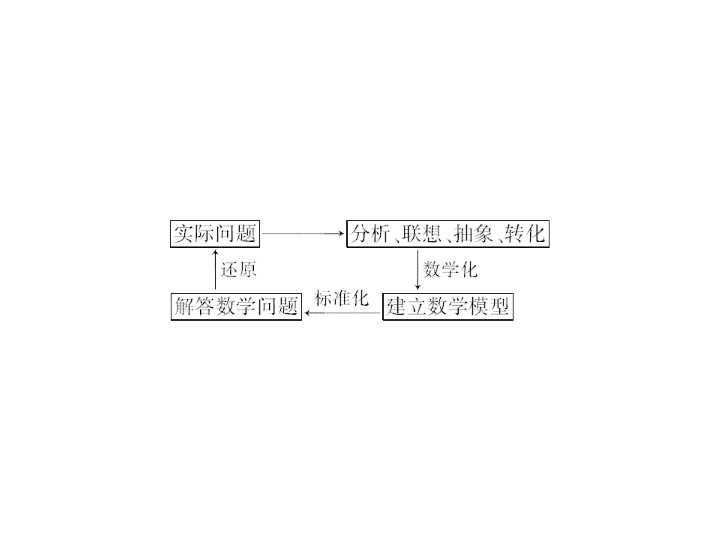
[ 最新考纲展示 ] 　 能在具体的问题情境中识别数列的等差关系或等比关系，并能用相关知识解决相应的问题． 第五节　数列的综合应用 数列综合应用题的解题步骤 1 ．审题 —— 弄清题意，分析涉及哪些数学内容，在每个数学内容中，各是什么问题． 2 ．分解 —— 把整个大题分解成几个小题或几个 “ 步骤 ” ，每个小题或每个 “ 步骤 ” 分别是数列问题、函数问题、解析几何问题、不等式问题等． 3 ．求解 —— 分别求解这些小题或这些 “ 步骤 ” ，从而得到整个问题的解答． 具体步骤如下框图： ____________________[ 通关方略 ]____________________ 数列的渗透力很强，它和函数、方程、三角形、不等式等知识相互联系，优化组合，无形中加大了综合的力度．解决此类题目，必须对蕴藏在数列概念和方法中的数学思想有所了解． 1 ．已知 log 2 x ， log 2 y, 2 成等差数列，则 M ( x ， y ) 的轨迹的图象为 ( 　　 ) 解析： 由于 log 2 x ， log 2 y, 2 成等差数列，则有 2log 2 y ＝ log 2 x ＋ 2 ，所以 y 2 ＝ 4 x . 又 y >0 ， x >0 ，故 M 的轨迹图象为 A. 答案： A 2 ．数列 1,1 ＋ 2,1 ＋ 2 ＋ 2 2, 1 ＋ 2 ＋ 2 2 ＋ 2 3 ， … ， 1 ＋ 2 ＋ 2 2 ＋ … ＋ 2 n － 1 ， … 的前 n 项和 S n ＞ 1 020 ，那么 n 的最小值是 ( 　　 ) A ． 7 　　　　 B ． 8 　　　　 C ． 9 　　　　 D ． 10 答案： D 常见的数列模型 1 ．等差数列模型：通过读题分析，由题意抽象出等差数列，利用等差数列有关知识解决问题． 2 ．等比数列模型：通过读题分析，由题意抽象出等比数列，利用等比数列有关知识解决问题． 3 ．递推公式模型：通过读题分析，由题意把所给条件用数列递推表达出来，然后通过分析递推关系式求解． 3 ．有一种细菌和一种病毒，每个细菌在每秒钟杀死一个病毒的同时将自身分裂为 2 个，现在有一个这样的细菌和 100 个这样的病毒，问细菌将病毒全部杀死至少需要 ( 　　 ) A ． 6 秒钟 B ． 7 秒钟 C ． 8 秒钟 D ． 9 秒钟 答案： B 4 ．等比数列 { a n } 的前 n 项和为 S n ，若 a 1 ＝ 1 ，且 4 a 1, 2 a 2 ， a 3 成等差数列，则 S 4 ＝ ________. 答案： 15 等差与等比数列的综合问题 【 例 1】 　 (2013 年高考浙江卷 ) 在公差为 d 的等差数列 { a n } 中，已知 a 1 ＝ 10 ，且 a 1, 2 a 2 ＋ 2,5 a 3 成等比数列． (1) 求 d ， a n ； (2) 若 d <0 ，求 | a 1 | ＋ | a 2 | ＋ | a 3 | ＋ … ＋ | a n |. [ 解析 ] 　 (1) 由题意得， 5 a 3 · a 1 ＝ (2 a 2 ＋ 2) 2 ，即 d 2 － 3 d － 4 ＝ 0 ， 故 d ＝－ 1 或 d ＝ 4. 所以 a n ＝－ n ＋ 11 ， n ∈ N * 或 a n ＝ 4 n ＋ 6 ， n ∈ N * . 反思总结 对于等差、等比数列的综合问题，应重点分析等差、等比数列的通项，前 n 项和以及等差、等比数列项之间的关系，往往用到转化与化归的思想方法． 答案： B 数列与函数的综合应用 【 例 2】 　已知函数 f ( x ) ＝ ln x 的图象是曲线 C ，点 A n ( a n ， f ( a n ))( n ∈ N * ) 是曲线 C 上的一系列点，曲线 C 在点 A n ( a n ， f ( a n )) 处的切线与 y 轴交于点 B n (0 ， b n ) ．若数列 { b n } 是公差为 2 的等差数列，且 f ( a 1 ) ＝ 3. (1) 分别求出数列 { a n } 与数列 { b n } 的通项公式； (2) 设 O 为坐标原点， S n 表示 △ OA n B n 的面积，求数列 { a n S n } 的前 n 项和 T n . 反思总结 解决函数与数列的综合问题应该注意的事项 (1) 数列是一类特殊的函数，它的图象是一群孤立的点； (2) 转化以函数为背景的条件时，应该注意题中的限制条件，如函数的定义域，这往往是很容易被忽视的问题； (3) 利用函数的方法研究数列中的相关问题时，应准确构造相应的函数，注意数列中相关限制条件的转化． 变式训练 2 ． (2013 年高考全国新课标卷 Ⅱ ) 等差数列 { a n } 的前 n 项和为 S n ，已知 S 10 ＝ 0 ， S 15 ＝ 25 ，则 nS n 的最小值为 ________ ． 答案： － 49 数列的实际应用 【 例 3】 　 (2014 年武汉调研 ) 某同学利用暑假时间到一家商场勤工俭学，该商场向他提供了三种付酬方案：第一种，每天支付 38 元；第二种，第一天付 4 元，第二天付 8 元，第三天付 12 元，依此类推；第三种，第一天付 0.4 元，以后每天支付的薪酬是前一天薪酬的 2 倍，工作时间为 n 天． (1) 设工作 n 天，记三种付酬方式薪酬总金额依次为 A n ， B n ， C n ，写出 A n ， B n ， C n 关于 n 的表达式； (2) 如果 n ＝ 10 ，你会选择哪种方式领取报酬？ (2) 由 (1) 得，当 n ＝ 10 时， A n ＝ 38 n ＝ 380 ， B n ＝ 2 n 2 ＋ 2 n ＝ 220 ， C n ＝ 0.4(2 10 － 1) ＝ 409.2. 所以 B 10 < A 10 < C 10 . 所以选择第三种付酬方式． 反思总结 求解数列应用问题，必须明确属于哪种数列模型，是等差数列，还是等比数列；是求通项问题，还是求项数问题，或者是求和问题．然后将题目中的量建立关系，利用数列模型去解决． 答案： C —— 数列与不等式的综合应用 数列与不等式的综合应用是高考考查的重点内容多以解答题形式考查，主要涉及不等式证明、大小比较以及不等式恒成立问题，解决时要注意转化思想的应用． 数列与不等式的证明问题 [ 解析 ] 　 (1) 由 S － ( n 2 ＋ n － 1) S n － ( n 2 ＋ n ) ＝ 0 ， 得 [ S n － ( n 2 ＋ n )]( S n ＋ 1) ＝ 0. 由于 { a n } 是正项数列，所以 S n >0 ， S n ＝ n 2 ＋ n . 于是 a 1 ＝ S 1 ＝ 2 ， n ≥ 2 时， a n ＝ S n － S n － 1 ＝ n 2 ＋ n － ( n － 1) 2 － ( n － 1) ＝ 2 n . 综上，数列 { a n } 的通项公式为 a n ＝ 2 n . 由题悟道 对于数列问题中求和类的不等式证明，如果是通过放缩的方法进行证明的，一般有两种类型：一种是能够直接求和，求和后再放缩 ( 如典例 1) ；一种是不能直接求和，需要放缩后才能求和，求和后再进行放缩 ( 如典例 2) ，在后一种类型中，一是要注意放缩的尺度，二是要注意从哪一项开始放缩． 数列与不等式恒成立问题 由题悟道 解此类问题关键在于将所求参数分离后转化为最值问题，在求最值时要充分注意定义域 n ∈ N * ，同时涉及 ( － 1) n 结构时要注意 n 的奇、偶性分类． 本小节结束 请按 ESC 键返回