2015年数学理高考课件1-3 简单的逻辑联结词、全称量词与存在量词

2015年数学理高考课件1-3 简单的逻辑联结词、全称量词与存在量词

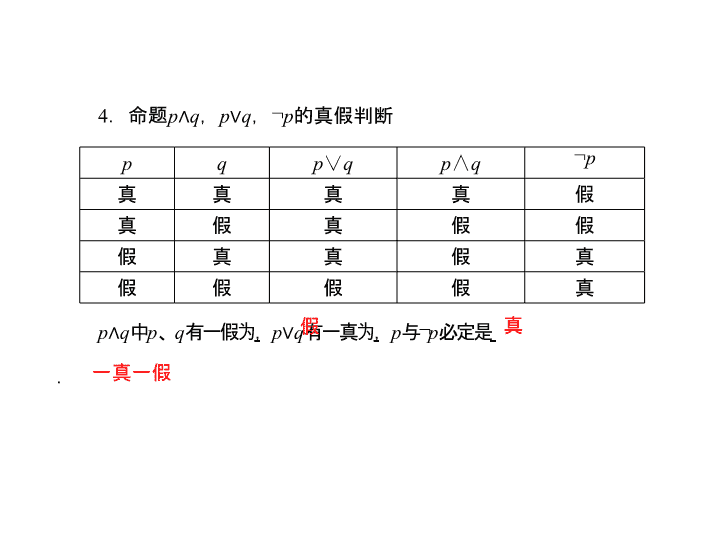
[ 最新考纲展示 ] 　 1 ． 了解逻辑联结词 “ 或 ” 、 “ 且 ” 、 “ 非 ” 的含义．　 2. 理解全称量词与存在量词的意义．　 3. 能正确地对含有一个量词的命题进行否定． 第三节　简单的逻辑联结词、全称量词与存在量词 简单的逻辑联结词 1 ．用联结词 “ 且 ” 联结命题 p 和命题 q ，记作 ，读作 “ ” ． 2 ．用联结词 “ 或 ” 联结命题 p 和命题 q ，记作 ，读作 “ ” ． 3 ．对一个命题 p 全盘否定记作 ，读作 “ 非 p ” 或 “ p 的否定 ” ． p ∧ q p 且 q p ∨ q p 或 q 綈 p 4 ．命题 p ∧ q ， p ∨ q ， 綈 p 的真假判断 p q p ∨ q p ∧ q 綈 p 真 真 真 真 假 真 假 真 假 假 假 真 真 假 真 假 假 假 假 真 p ∧ q 中 p 、 q 有一假为 ， p ∨ q 有一真为 ， p 与 綈 p 必定是 ． 假 真 一真一假 ____________________[ 通关方略 ]____________________ 逻辑联结词 “ 且 ”“ 或 ”“ 非 ” 与集合运算中的 “ 交 ”“ 并 ”“ 补 ” 的关系： “ 且 ”“ 或 ”“ 非 ” 三个逻辑联结词，对应着集合运算中的 “ 交 ”“ 并 ”“ 补 ” ，因此，常常借助集合的 “ 交 ”“ 并 ”“ 补 ” 的意义来解答由 “ 且 ”“ 或 ”“ 非 ” 三个联结词构成的命题问题． 答案： B 全称量词与存在量词 1 ．全称量词与全称命题 (1) 短语 “ ” 、 “ ” 等在逻辑中通常叫做全称量词，并用符号 “ ” 表示； (2) 含有 的命题，叫做全称命题； (3) 全称命题 “ 对 M 中任意一个 x ，有 p ( x ) 成立 ” 可用符号简记为： ，读作 “ ” ． 所有的 任意一个 ∀ 全称量词 ∀ x ∈ M ， p ( x ) 对任意 x 属于 M ，有 p ( x ) 成立 2 ．存在量词与特称命题 (1) 短语 “ ” 、 “ ” 等在逻辑中通常叫做存在量词，并用符号 “ ” 表示； (2) 含有 的命题，叫做特称命题； (3) 特称命题 “ 存在 M 中的一个 x 0 ，使 p ( x 0 ) 成立 ” 可用符号简记为： ，读作 “ ” ． 存在一个 至少有一个 ∃ 存在量词 ∃ x 0 ∈ M ， p ( x 0 ) 存在一个 x 0 属于 M ，使 p ( x 0 ) 成立 ____________________[ 通关方略 ]____________________ 对于同一个全称命题或特称命题，由于自然语言的不同，可以有不同的表述方法，在实际应用中可以灵活选择，如下表所示： 表述方法 全称命题 ( ∀ x ∈ M ， p ( x )) 特称命题 ( ∃ x 0 ∈ M ， q ( x 0 )) 对所有的 x ∈ M ， p ( x ) 成立 存在 x 0 ∈ M ， q ( x 0 ) 成立 对一切 x ∈ M ， p ( x ) 成立 至少有一个 x 0 ∈ M ， q ( x 0 ) 成立 对每一个 x 0 ∈ M ， p ( x 0 ) 成立 对有些 x 0 ∈ M ， q ( x 0 ) 成立 任选一个 x 0 ∈ M ， p ( x 0 ) 成立 对某个 x 0 ∈ M ， q ( x 0 ) 成立 2 ．将 a 2 ＋ b 2 ＋ 2 ab ＝ ( a ＋ b ) 2 改写成全称命题是 ( 　　 ) A ． ∃ a ， b ∈ R ， a 2 ＋ b 2 ＋ 2 ab ＝ ( a ＋ b ) 2 B ． ∃ a <0 ， b >0 ， a 2 ＋ b 2 ＋ 2 ab ＝ ( a ＋ b ) 2 C ． ∀ a >0 ， b >0 ， a 2 ＋ b 2 ＋ 2 ab ＝ ( a ＋ b ) 2 D ． ∀ a ， b ∈ R ， a 2 ＋ b 2 ＋ 2 ab ＝ ( a ＋ b ) 2 解析： 全称命题含有量词 “ ∀ ” ，故排除 A 、 B ，又等式 a 2 ＋ b 2 ＋ 2 ab ＝ ( a ＋ b ) 2 对于全体实数都成立． 答案： D 答案： B 含有一个量词的命题的否定 全称命题的否定是特称命题，特称命题的否定是全称命题，如下所示： 命　题 命题的否定 ∀ x ∈ M ， p ( x ) __________________ ∃ x 0 ∈ M ， p ( x 0 ) _________________ ∃ x 0 ∈ M ， 綈 p ( x 0 ) ∀ x ∈ M ， 綈 p ( x ) ____________________[ 通关方略 ]____________________ 复合命题的否定如下： (1)“ 綈 p ” 的否定是“ p ” ． (2)“ p ∨ q ” 的否定是“ ( 綈 p ) ∧ ( 綈 q )” ． (3)“ p ∧ q ” 的否定是“ ( 綈 p ) ∨ ( 綈 q )” ． 4 ． (1) 命题 p ：任意两个等边三角形都是相似的，则 綈 p ： ________________________________________________________________________. 解析： (1) 全称命题的否定为特称命题，则 綈 p ：存在两个等边三角形，它们不相似． (2) 特称命题的否定为全称命题，则 綈 p ： ∀ x ∈ R ， x 2 ＋ 2 x ＋ 2≠0 答案： (1) 存在两个等边三角形，它们不相似 (2) ∀ x ∈ R ， x 2 ＋ 2 x ＋ 2≠0 含有逻辑联结词的命题的真假判断 【 例 1】 　 (2013 年高考湖北卷 ) 在一次跳伞训练中，甲、乙两位学员各跳一次．设命题 p 是 “ 甲降落在指定范围 ” ， q 是 “ 乙降落在指定范围 ” ，则命题 “ 至少有一位学员没有降落在指定范围 ” 可表示为 ( 　　 ) A ． ( 綈 p ) ∨ ( 綈 q ) 　　　　　 B ． p ∨ ( 綈 q ) C ． ( 綈 p ) ∧ ( 綈 q ) D ． p ∨ q [ 解析 ] 　 由题意可知， “ 至少有一位学员没有降落在指定范围 ” 意味着 “ 甲没有或乙没有降落在指定范围 ” ，使用 “ 非 ” 和 “ 或 ” 联结词即可表示该复合命题为 ( 綈 p ) ∨ ( 綈 q ) ． [ 答案 ] 　 A 反思总结 正确理解逻辑联结词 “ 或 ” 、 “ 且 ” 、 “ 非 ” 的含义是关键，解题时应根据组成各个复合命题的语句中所出现的逻辑联结词进行命题结构与真假的判断．其步骤为： ① 确定复合命题的构成形式； ② 判断其中简单命题的真假； ③ 判断复合命题的真假． 答案： C 全称命题、特称命题的真假判断 【 例 2】 　 (2014 年济南模拟 ) 下列命题中是假命题的是 ( 　　 ) A ． ∃ α ， β ∈ R ，使 sin ( α ＋ β ) ＝ sin α ＋ sin β B ． ∀ φ ∈ R ，函数 f ( x ) ＝ sin(2 x ＋ φ ) 都不是偶函数 C ． ∃ m ∈ R ，使 f ( x ) ＝ ( m － 1) · xm 2 － 4 m ＋ 3 是幂函数，且在 (0 ，＋ ∞ ) 上单调递减 D ． ∀ a >0 ，函数 f ( x ) ＝ ln 2 x ＋ ln x － a 有零点 [ 答案 ] 　 B 反思总结 1 ． 全称命题真假的判断方法 (1) 要判断一个全称命题是真命题，必须对限定的集合 M 中的每一个元素 x ，证明 p ( x ) 成立． (2) 要判断一个全称命题是假命题，只要能举出集合 M 中的一个特殊值 x ＝ x 0 ，使 p ( x 0 ) 不成立即可． 2 ．特称命题真假的判断方法 要判断一个特称命题是真命题，只要在限定的集合 M 中，找到一个 x ＝ x 0 ，使 p ( x 0 ) 成立即可，否则这一特称命题就是假命题． 解析： 易知 |sin x | ≤ 1 ，故 A 是假命题． 答案： A 含有一个量词的命题否定 【 例 3】 　 (2013 年高考四川卷 ) 设 x ∈ Z ，集合 A 是奇数集，集合 B 是偶数集，若命题 p ： ∀ x ∈ A, 2 x ∈ B ，则 ( 　　 ) A ． 綈 p ： ∀ x ∈ A, 2 x ∉ B B ． 綈 p ： ∀ x ∉ A, 2 x ∉ B C ． 綈 p ： ∃ x ∉ A, 2 x ∈ B D ． 綈 p ： ∃ x ∈ A, 2 x ∉ B [ 解析 ] 　 因为任意都满足的否定是存在不满足的，所以选 D. [ 答案 ] 　 D 反思总结 对含有一个量词的命题进行否定的方法：一般地，写含有一个量词的命题的否定，首先要明确这个命题是全称命题还是特称命题，并找到其量词的位置及相应结论，然后把命题中的全称量词改成存在量词，存在量词改成全称量词，同时否定结论． 答案： C —— 由命题真假求参数范围问题 已知命题的真假求参数的范围是考查的热点内容．此类题目，能力要求较高，综合性强，常见的命题角度有： (1) 利用复合命题的真假求参数范围． (2) 利用全称 ( 特称 ) 命题的真假求参数范围． 利用复合命题的真假求参数范围 【 典例 1】 　已知命题 p ：关于 x 的方程 x 2 － ax ＋ 4 ＝ 0 有实根；命题 q ：关于 x 的函数 y ＝ 2 x 2 ＋ ax ＋ 4 在 [3 ，＋ ∞ ) 上是增函数．若 p ∨ q 是真命题， p ∧ q 是假命题，则实数 a 的取值范围是 ( 　　 ) A ． ( － 12 ，－ 4] ∪ [4 ，＋ ∞ ) B ． [ － 12 ，－ 4] ∪ [4 ，＋ ∞ ) C ． ( － ∞ ，－ 12) ∪ ( － 4,4) D ． [ － 12 ，＋ ∞ ) [ 答案 ] 　 C 解题模板 　 第一步：确定 p 、 q 命题为真时参数范围 第二步：由条件判断 p 、 q 真假情况 第三步：根据 p 、 q 真假求参数范围 第四步：反思解题过程 利用全称 ( 特称 ) 命题的真假求参数范围 【 典例 2】 　若命题 p ： ∃ x ∈ R ， ax 2 ＋ 4 x ＋ a < － 2 x 2 ＋ 1 是假命题，则实数 a 的取值范围是 ________ ． [ 答案 ] 　 [2 ，＋∞ ) 解题模板 　 第一步：转化：根据条件命题的真假进行转化 第二步：求范围：根据转化问题，数形结合求参数范围 第三步：结论：回答问题结论 第四步：反思：反思解题过程，注意端点值验证取舍 设集合 A ＝ { ( x ， y )|( x － 4) 2 ＋ y 2 ＝ 1} ， B ＝ {( x ， y )|( x － t ) 2 ＋ ( y － at ＋ 2) 2 ＝ 1} ，如果命题 “ ∃ t ∈ R ， A ∩ B ≠ ∅ ” 是真命题，则实数 a 的取值范围是 ________ ． 本小节结束 请按 ESC 键返回