浙江省2021届高考数学一轮复习第三章函数概念及基本初等函数Ⅰ第7节函数的图象与变换课件

浙江省2021届高考数学一轮复习第三章函数概念及基本初等函数Ⅰ第7节函数的图象与变换课件

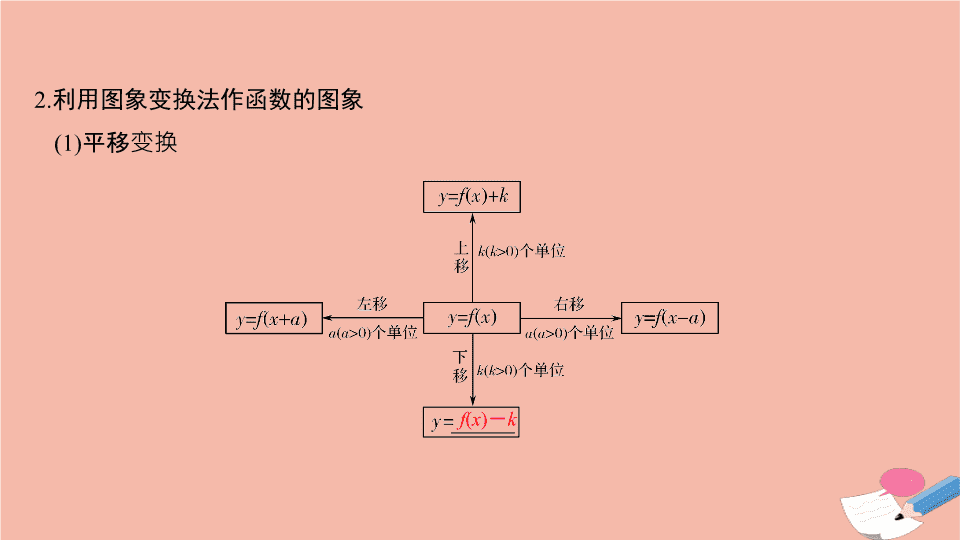
第 7 节　函数的图象与变换 考试要求　 1. 在实际情境中，会根据不同的需要选择恰当的方法 ( 如图象法、列表法、解析法 ) 表示函数； 2. 会运用基本初等函数的图象分析函数的性质，并运用函数的图象解简单的方程 ( 不等式 ) 问题 . 知 识 梳 理 1 . 利用描点法作函数的图象 步骤： (1) 确定函数的定义域； (2) 化简函数解析式； (3) 讨论函数的性质 ( 奇偶性、单调性、周期性、对称性等 ) ； (4) 列表 ( 尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等 ) ，描点，连线 . 2 . 利用图象变换法作函数的图象 (1) 平移变换 f ( x ) － k － f ( x ) f ( － x ) － f ( － x ) log a x | f ( x )| f (| x |) 诊 断 自 测 1. 判断下列说法的正误 . (1) 函数 y ＝ f (1 － x ) 的图象，可由 y ＝ f ( － x ) 的图象向左平移 1 个单位得到 .( 　　 ) (2) 函数 y ＝ f ( x ) 的图象关于 y 轴对称即函数 y ＝ f ( x ) 与 y ＝ f ( － x ) 的图象关于 y 轴对称 .( 　　 ) (3) 当 x ∈ (0 ，＋ ∞ ) 时，函数 y ＝ f (| x |) 的图象与 y ＝ | f ( x )| 的图象相同 .( 　　 ) (4) 若函数 y ＝ f ( x ) 满足 f (1 ＋ x ) ＝ f (1 － x ) ，则函数 f ( x ) 的图象关于直线 x ＝ 1 对称 .( 　　 ) 解析 　 (1) y ＝ f ( － x ) 的图象向左平移 1 个单位得到 y ＝ f ( － 1 － x ) 的图象，故 (1) 错 . (2) 两种说法有本质不同，前者为函数的图象自身关于 y 轴对称，后者是两个函数的图象关于 y 轴对称，故 (2) 错 . (3) 令 f ( x ) ＝－ x ，当 x ∈ (0 ，＋ ∞ ) 时， y ＝ | f ( x )| ＝ x ， y ＝ f (| x |) ＝－ x ，两函数图象不同，故 (3) 错 . 答案 　 (1) × 　 (2) × 　 (3) × 　 (4) √ 2. 函数 f ( x ) 的图象向右平移 1 个单位长度，所得图象与曲线 y ＝ e x 关于 y 轴对称，则 f ( x ) 的解析式为 ( 　　 ) A. f ( x ) ＝ e x ＋ 1 B. f ( x ) ＝ e x － 1 C. f ( x ) ＝ e － x ＋ 1 D. f ( x ) ＝ e － x － 1 解析　 依题意，与曲线 y ＝ e x 关于 y 轴对称的曲线是 y ＝ e － x ，于是 f ( x ) 相当于 y ＝ e － x 向左平移 1 个单位的结果， ∴ f ( x ) ＝ e － ( x ＋ 1) ＝ e － x － 1 . 答案　 D 3. (2019· 浙江名师预测卷 ) 函数 y ＝ (e x － e － x )sin|2 x | 的图象可能是 ( 　　 ) 答案　 A 4. 若函数 y ＝ f ( x ) 在 x ∈ [ － 2 ， 2] 的图象如图所示，则当 x ∈ [ － 2 ， 2] 时， f ( x ) ＋ f ( － x ) ＝ ________. 解析　 由于 y ＝ f ( x ) 的图象关于原点对称， ∴ f ( x ) ＋ f ( － x ) ＝ f ( x ) － f ( x ) ＝ 0. 答案　 0 5. 若关于 x 的方程 | x | ＝ a － x 只有一个解，则实数 a 的取值范围是 ________. 解析　 在同一个坐标系中画出函数 y ＝ | x | 与 y ＝ a － x 的图象，如图所示 . 由图象知当 a >0 时，方程 | x | ＝ a － x 只有一个解 . 答案　 (0 ，＋ ∞ ) 6. 已知函数 f ( x ) ＝ 2 x ，若函数 g ( x ) 的图象与 f ( x ) 的图象关于 x 轴对称，则 g ( x ) ＝ ________ ；若把函数 f ( x ) 的图象向左平移 1 个单位，再向下平移 4 个单位后，所得函数的解析式为 h ( x ) ＝ ________. 解析　 ∵ g ( x ) 的图象与函数 f ( x ) ＝ 2 x 的图象关于 x 轴对称， ∴ g ( x ) ＝－ 2 x . 把 f ( x ) ＝ 2 x 的图象向左平移 1 个单位，得 m ( x ) ＝ 2 x ＋ 1 的图象，再向下平移 4 个单位，得 h ( x ) ＝ 2 x ＋ 1 － 4 的图象 . 答案 　－ 2 x 　 2 x ＋ 1 － 4 考点一　作函数的图象 (2) 将函数 y ＝ log 2 x 的图象向左平移一个单位，再将 x 轴下方的部分沿 x 轴翻折上去，即可得到函数 y ＝ |log 2 ( x ＋ 1)| 的图象，如图 ② . 规律方法 　画函数图象的一般方法 (1) 直接法 . 当函数解析式 ( 或变形后的解析式 ) 是熟悉的基本函数时，就可根据这些函数的特征描出图象的关键点直接作出 . (2) 图象变换法 . 若函数图象可由某个基本函数的图象经过平移、翻折、对称得到，可利用图象变换作出，并应注意平移变换与伸缩变换的顺序对变换单位及解析式的影响 . 【训练 1 】 分别画出下列函数的图象： (1) y ＝ |lg x | ； (2) y ＝ sin | x |. ∴ 函数 y ＝ |lg x | 的图象，如图 ① . (2) 当 x ≥ 0 时， y ＝ sin| x | 与 y ＝ sin x 的图象完全相同，又 y ＝ sin| x | 为偶函数，图象关于 y 轴对称，其图象如图 ② . 考点二　函数图象的辨识 A. ①④②③ B. ①④③② C. ③②④① D. ③④②① 答案　 (1)D 　 (2)C 规律方法　 (1) 抓住函数的性质，定性分析 ① 从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置 . ② 从函数的单调性，判断图象的变化趋势； ③ 从周期性，判断图象的循环往复 . ④ 从函数的奇偶性，判断图象的对称性 . (2) 抓住函数的特征，定量计算 从函数的特征点，利用特征点、特殊值的计算分析解决问题 . 【训练 2 】 (1) (2019· 浙江名校新高考研究联盟三联 ) 已知某函数图象如图所示，则此函数的解析式可能是 ( 　　 ) (2) 函数 y ＝ 2 x 2 － e | x | 在 [ － 2 ， 2] 的图象大致为 ( 　　 ) (2) f ( x ) ＝ 2 x 2 － e | x | ， x ∈ [ － 2 ， 2] 是偶函数，又 f (2) ＝ 8 － e 2 ∈ (0 ， 1) ，排除 A ， B. 设 g ( x ) ＝ 2 x 2 － e x ， x ≥ 0 ，则 g ′( x ) ＝ 4 x － e x . 又 g ′(0) ＜ 0 ， g ′(2) ＞ 0 ， ∴ g ( x ) 在 (0 ， 2) 内至少存在一个极值点， ∴ f ( x ) ＝ 2 x 2 － e | x | 在 (0 ， 2) 内至少存在一个极值点，排除 C ，故选 D. 答案　 (1)A 　 (2)D 考点三　函数图象的应用 【例 3 － 1 】 ( 一题多解 ) 设函数 f ( x ) ＝ min{| x － 2| ， x 2 ， | x ＋ 2|} ，其中 min{ x ， y ， z } 表示 x ， y ， z 中的最小者 . 下列说法错误的是 ( 　　 ) A. 函数 f ( x ) 为偶函数 B. 若 x ∈ [1 ，＋ ∞ ) 时，有 f ( x － 2) ≤ f ( x ) C. 若 x ∈ R 时， f ( f ( x )) ≤ f ( x ) D. 若 x ∈ [ － 4 ， 4] 时， | f ( x ) － 2| ≥ f ( x ) 多维探究 解析　法一　 由 f ( x ) ＝ min{| x － 2| ， x 2 ， | x ＋ 2|} ，得 f ( － x ) ＝ min{| － x － 2| ， ( － x ) 2 ， | － x ＋ 2|} ＝ f ( x ) ，即函数 f ( x ) 为偶函数；如图，作出函数 f ( x ) 的图象，将 f ( x ) 的图象向右平移 2 个单位长度知 f ( x － 2) 的图象在 [1 ，＋ ∞ ) 上的部分位于 f ( x ) 的图象的下方，则有 f ( x － 2) ≤ f ( x ) ；令 f ( x ) ＝ u ≥ 0 ，则由图象知 f ( u ) ≤ u ，由排除法知 D 错误，故选 D. 法二　 若 x ∈ [ － 4 ， 4] ，则 0 ≤ f ( x ) ≤ 2 ，故 | f ( x ) － 2| ＝ 2 － f ( x ) ≥ f ( x ) 等价于 0 ≤ f ( x ) ≤ 1 ，所以当 x ∈ [ － 4 ， 4] 时， | f ( x ) － 2| ≥ f ( x ) 不恒成立 . 否定一个结论，只需给出一个反例即可 . 取 x ＝ 4 ，则 | f (4) － 2| ＝ 0< f (4) ， D 错误，故选 D. 答案　 D 角度 2 　研究函数零点 ( 或方程根 ) 的个数 答案　 (1 ， 3] 角度 3 　求不等式的解集 规律方法 　 (1) 利用函数的图象研究函数的性质，一定要注意其对应关系，如图象的左右范围对应定义域，上下范围对应值域，上升、下降趋势对应单调性，对称性对应奇偶性 . (2) 研究方程根的个数或由方程根的个数确定参数的值 ( 范围 ) ：构造函数，转化为两函数图象的交点个数问题，在同一坐标系中分别作出两函数的图象，数形结合求解 . (3) 研究不等式的解：当不等式问题不能用代数法求解，但其对应函数的图象可作出时，常将不等式问题转化为两函数图象的上、下关系问题，从而利用数形结合求解 . (3) ( 角度 3) 已知函数 y ＝ f ( x ) 的图象是圆 x 2 ＋ y 2 ＝ 2 上的两段弧，如图所示，则不等式 f ( x )> f ( － x ) － 2 x 的解集是 ______. ① 若 0 ＜ m ≤ 1 ，两函数的图象如图 1 所示，可知两函数在 x ∈ [0 ， 1] 上有且只有 1 个交点，符合题意 . ② 若 m ＞ 1 ，两函数的大致图象如图 2 所示 . 为使两函数图象在 x ∈ [0 ， 1] 上有且只有 1 个交点，只需 ( m － 1) 2 ≥ 1 ＋ m ，得 m ≥ 3 或 m ≤ 0( 舍去 ). 综上， m ∈ (0 ， 1] ∪ [3 ，＋ ∞ ).