河北省石家庄市第二中学2019-2020学年高二上学期期中考试数学试题

河北省石家庄市第二中学2019-2020学年高二上学期期中考试数学试题

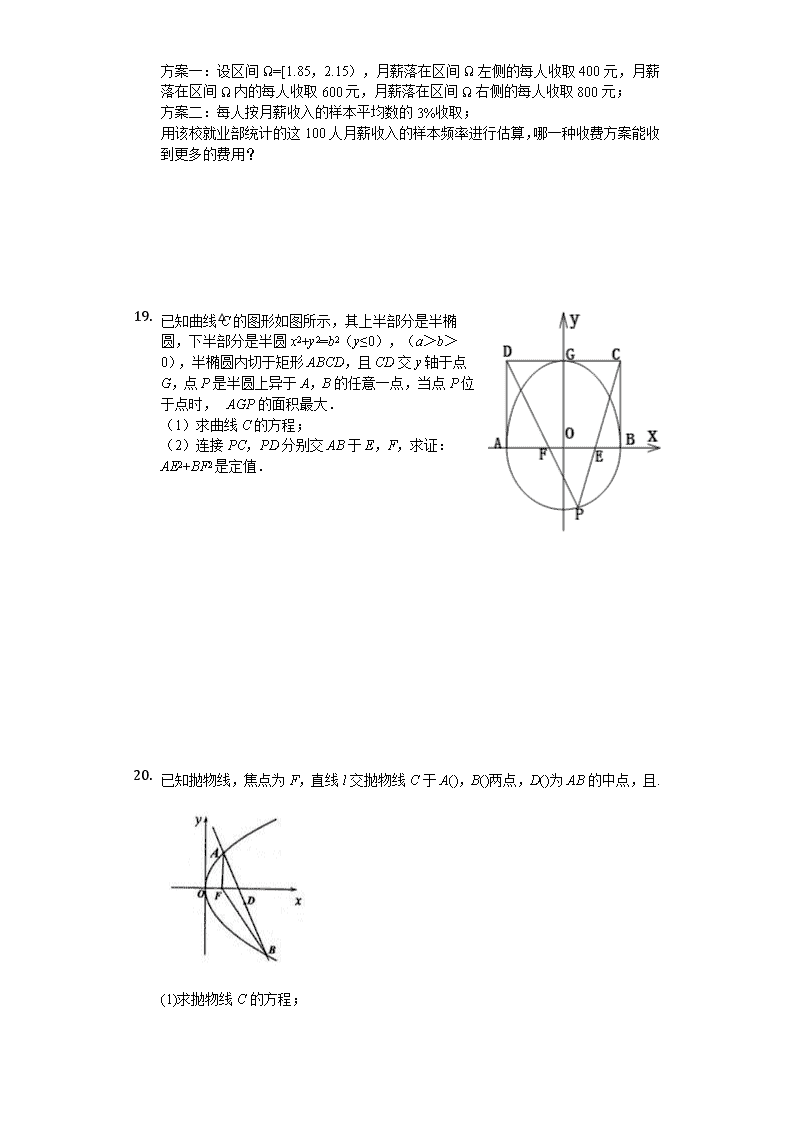
河北省石家庄市第二中学2019-2020学年高二上学期期中考试数学试题 一、选择题（本大题共12小题）‎ 1. 已知条件p：x＞1，q：，则p是q的（　　）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 2. 已知双曲线的实轴长为8，则该双曲线的渐近线的斜率为（　　）‎ A. B. C. D. ‎ 3. 小波一星期的总开支分布图如图(1)所示，一星期的食品开支如图(2)所示，则小波一星期的鸡蛋开支占总开支的百分比为（）‎ A. B. C. D. 不能确定 4. 下列有关命题的说法正确的是（　　）‎ A. 命题“若,则”的否命题为“若,则” B. “”是“”的必要不充分条件 C. 命题“,”的否定是“,” D. 命题“若,则”的逆否命题为真命题 5. 若椭圆上一点到两焦点的距离之和为m-3，则m的值为（　　）‎ A. 1 B. ‎7 ‎C. 9 D. 7或9‎ 6. 若点A，B是椭圆上关于原点对称的两点，F是椭圆的右焦点，则△ABF面积的最大值是（　　）‎ A. 4 B. C. D. ‎ 7. 过抛物线y2=2px（p＞0）的焦点F作直线交抛物线于A、B两点，O为抛物线的顶点．则△ABO是一个（　　）‎ A. 等边三角形 B. 直角三角形 C. 不等边锐角三角形 D. 钝角三角形 8. 已知点P是椭圆=1（xy≠0）上的动点，F1，F2分别是椭圆的左，右焦点，O为原点，若M是∠F1PF2的角平分线上的一点，且F‎1M⊥MP，则OM的长度取值范围（　　）‎ A. B. C. D. ‎ 9. 如图，过抛物线y2=2px（p＞0）的焦点F的直线交抛物线于点A、B，交其准线l于点C，若点F是AC的中点，且|AF|=4，则线段AB的长为（　　）‎ A. 5 B. ‎6 ‎C. D. ‎ ‎ ‎ 1. 已知双曲线E：-=1（a＞0，b＞0），过原点任作一条直线，分别交双曲线两支于点P，Q（点P在第一象限），点F为E的左焦点，且满足|PF|=3|FQ|，|OP|=b，则E的离心率为（　　）‎ A. B. C. 2 D. ‎ 2. 已知F1，F2为椭圆的左、右焦点，M为椭圆上一点，若满足△MF‎1F2内切圆的周长等于3π的点M恰好有2个，则a2=（　　）‎ A. 20 B. ‎25 ‎C. 36 D. 48‎ 3. 已知点F1，F2分别是双曲线的左、右焦点，O为坐标原点，点P在双曲线C的右支上，且满足|F‎1F2|=2|OP|，tan∠PF‎2F1≥4，则双曲线C的离心率的取值范围为（　　）‎ A. B. C. D. ‎ 二、填空题（本大题共4小题）‎ 4. 若抛物线过点（-1，3），则抛物线的标准方程为______．‎ 5. 已知点P是椭圆＋＝1(a＞b＞0)上的一点，F1，F2分别为椭圆的左、右焦点，已知∠F1PF2＝120°，且|PF1|＝3|PF2|，则椭圆的离心率为___________．‎ 6. 双曲线是等轴双曲线，点P为其右支上一动点，若点P到直线x-y+1=0的距离大于m恒成立，则实数m的最大值为______．‎ 7. 已知抛物线和所围成的封闭曲线，给定点A（0，a），若在此封闭曲线上恰有三对不同的点，满足每一对点关于点A对称，则实数a的取值范围是______．‎ 三、解答题（本大题共6小题）‎ 8. 设命题p：函数f（x）=x2-ax在[0，+∞）单调递增；命题q：方程x2+ay2=2表示焦点在y轴上的椭圆．命题“p∨q”为真命题，“p∧q”为假命题，求实数a的取值范围． ‎ 9. 某“双一流A类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查，其中一项是他们的月薪收入情况，调查发现，他们的月薪收入在人民币1.65万元到2.35万元之间，根据统计数据分组，得到如图的频率分布直方图： （1）将同一组数据用该区间的中点值作代表，求这100人月薪收入的样本平均数； （2）该校在某地区就业的2018届本科毕业生共50人，决定于2019‎ 国庆长假期间举办一次同学联谊会，并收取一定的活动费用，有两种收费方案： 方案一：设区间Ω=[1.85，2.15），月薪落在区间Ω左侧的每人收取400元，月薪落在区间Ω内的每人收取600元，月薪落在区间Ω右侧的每人收取800元； 方案二：每人按月薪收入的样本平均数的3%收取； 用该校就业部统计的这100人月薪收入的样本频率进行估算，哪一种收费方案能收到更多的费用？ ‎ 1. 已知曲线C的图形如图所示，其上半部分是半椭圆，下半部分是半圆x2+y2=b2（y≤0），（a＞b＞0），半椭圆内切于矩形ABCD，且CD交y轴于点G，点P是半圆上异于A，B的任意一点，当点P位于点时，△AGP的面积最大． （1）求曲线C的方程； （2）连接PC，PD分别交AB于E，F，求证：AE2+BF2是定值． ‎ ‎ ‎ 2. 已知抛物线，焦点为F，直线l交抛物线C于A()，B()两点，D()为AB的中点，且.‎ ‎(1)求抛物线C的方程；‎ ‎(2)若，求的最小值. ‎ 1. 已知椭圆方程C为：+=1．（a＞b＞0）椭圆的右焦点为（1，0），离心率为e=，直线l：y=kx+m与椭圆C相交于A、B两点，且KOAKOB=-． （I）求椭圆的C的方程； （Ⅱ）求△AOB的面积． ‎ 2. 已知抛物线C：y2=2px（p＞0）的焦点为F，A为C上异于原点的任意一点，过点A的直线l交C于另一点B，交x轴的正半轴于点D，且有|FA|=|FD|，当点A的横坐标为3时，△ADF为正三角形． （Ⅰ）求C的方程； （Ⅱ）若直线l1∥l，且l1和C有且只有一个公共点E，试问直线AE是否过定点，若过定点，求出定点坐标；若不过定点，请说明理由． ‎ 答案和解析 ‎1.【答案】A ‎ ‎【解析】解：由x＞1，推出＜1，p是q的充分条件， 由＜1，得＜0，解得：x＜0或x＞1．不是必要条件， 故选：A． 根据充分必要条件的定义，分别证明其充分性和必要性，从而得到答案． 本题考查了充分必要条件，考查了不等式的解法，是一道基础题． 2.【答案】C ‎ ‎【解析】解：双曲线的实轴长为8， 可得：m2+12=16，解得m=2，m=-2（舍去）． 所以，双曲线的渐近线方程为：±=0． 则该双曲线的渐近线的斜率：±． 故选：C． 求出双曲线的实轴长，得到m，然后求解双曲线的渐近线方程，得到渐近线的斜率即可． 本题考查双曲线的简单性质的应用，是基本知识的考查，是基础题． 3.【答案】C ‎ ‎【解析】​【分析】 ​本题考查分布的意义和作用，考查学生的读图能力，属于基础题． 计算鸡蛋占食品开支的百分比，利用一星期的食品开支占总开支的百分比，即可求得一星期的鸡蛋开支占总开支的百分比. 【解答】 解：根据一星期的食品开支图，可知鸡蛋占食品开支的百分比为%， ∵一星期的食品开支占总开支的百分比为30%， ∴一星期的鸡蛋开支占总开支的百分比为30%×10%=3%． 故选C． 4.【答案】D ‎ ‎【解析】解：对于A，命题“若x2=1，则x=‎1”‎的否命题为“若x2≠1，则x≠‎1”‎，故错； 对于B，∵方程x2-5x-6=0的根为-1或6，故“x=-1”是“x2-5x-6=‎0”‎的充分不必要条件，故错； 对于C，命题“”的否定是“∀x∈R，x2+x+1≥‎0”‎，故错； 对于D，命题“若x=y，则sinx=siny”为真命题，其逆否命题与原命题同真假，故为真命题，故正确； 故选：D． A，命题“若x2=1，则x=‎1”‎的否命题为“若x2≠1，则x≠‎1”‎； B，由方程x2-5x-6=0的根为-1或6，知“x=-1”是“x2-5x-6=‎0”‎的充分不必要条件； C，命题“”的否定是“∀x∈R，x2+x+1≥‎0”‎； D，原命题为真命题，其逆否命题与原命题同真假， 本题考查了命题真假的判定，属于基础题． ‎ ‎5.【答案】C ‎ ‎【解析】解：根据题意，对于椭圆，分2种情况讨论： ①，椭圆的焦点在x轴上，有4＞m，则a=2， 若椭圆上一点到两个焦点的距离之和为m-3， 则有‎2a=m-3=4，解可得m=7， 又由4＞m， m=7不合题意，舍去； ②，椭圆的焦点在y轴上，有4＜m，则a=， 若椭圆上一点到两个焦点的距离之和为m-3， 则有‎2a=m-3=2， 解可得：m=9或m=-1（舍） 故m=9， 故选：C． 根据题意，按椭圆的焦点位置分2种情况讨论，结合椭圆的定义分析可得m的值． 本题考查椭圆的几何性质，涉及椭圆的离心率计算公式，关键是求出m的值，是中档题． 6.【答案】D ‎ ‎【解析】解：△ABF面积等于△AOF 和△BOF 的面积之和， 设A到x轴的距离为h，由AB为过椭圆中心的弦，则B到x轴的距离也为h， ∴△AOF 和△BOF的面积相等，故△ABF面积等于×c×2h=ch，又h的最大值为b， 椭圆可知a=2，b=1，c=． ∴△ABF面积的最大值是bc=， 故选：D． △ABF面积等于△AOF 和△BOF 的面积之和，△AOF 和△BOF 的面积相等，A到x轴的距离h应最大，又h的最大值为b，从而得到△ABF面积的最大值． 本题考查椭圆的简单性质，用分割法求△ABF的面积，利用△AOF 和△BOF 是同底等高的两个三角形． 7.【答案】D ‎ ‎【解析】解：设A（x1，y1），B（x2，y2），AB方程 由，得y2-2pmy-p2=0，∴ ∴= ∴，∴∠AOB为钝角，△ABO为钝角三角形 故选：D． 设出A，B点坐标，以及直线AB的方程，联立直线方程与抛物线方程，用向量的坐标公式求再代入向量的夹角公式，求出∠AOB的余弦值，再判断正负即可． 本题考查了直线与抛物线的位置关系，关键是用坐标表示向量的数量积． 8.【答案】B ‎ ‎【解析】解：如图，延长PF2、F‎1M，交与N点，连接OM， ∵PM是∠F1PF2平分线，F‎1M⊥MP， ∴|PN|=|PF1|，M为F‎1F2中点， ∵O为F‎1F2中点，M为F1N中点 ∴|OM|=|F2N|=||PN|-|PF2||=||PF1|-|PF2|| 设P点坐标为（x0，y0）， ∵在椭圆=1中，离心率e==， 由圆锥曲线的第二定义，得|PF1|=a+ex0，|PF2|=a-ex0， ∴||PF1|-|PF2||=|a+ex0-a+ex0|=|2ex0|=|x0| ∵P点在椭圆=1上， ∴|x0|∈[0，4]， 又∵x≠0，y≠0，可得|x0|∈（0，4）， ∴|OM|∈（0，2）， ∴OM的长度取值范围是（0，2）． 故答案选：B． 延长PF2、F‎1M，交与N点，连接OM，利用等腰三角形的性质、三角形中位线定理和椭圆的定义，证出|OM|=||PF1|-|PF2||．再利用圆锥曲线的统一定义，化简得||PF1|-|PF2||=|x0|，利用椭圆上点横坐标的范围结合已知数据即可算出OM的长度取值范围． 本题求两点间的距离的取值范围，着重考查了椭圆的定义、等腰三角形的性质、三角形中位线定理和椭圆的简单几何性质等知识，属于中档题． 9.【答案】C ‎ ‎【解析】【分析】 本题考查抛物线的定义及其应用，抛物线的几何性质，过焦点的弦的弦长关系，平面几何知识，转化化归的思想方法，属中档题 设A、B在准线上的射影分别为为M、N，准线与横轴交于点H，则FH=p，由点F是AC的中点，得p=2，设BF=BN=x，则，即，解得x=，即可求解． 【解答】 解：设A、B在准线上的射影分别为为M、N，准线与横轴交于点H，则FH=p， 由于点F是AC的中点，|AF|=4，∴AM=4=2p，∴p=2， 设BF=BN=x，则，即，解得x= ∴， 故选：C． ‎ ‎​ 10.【答案】B ‎ ‎【解析】解：由题意可知：双曲线的右焦点F1，由P关于原点的对称点为Q， 则|OP|=|OQ|， ∴四边形PFQF1为平行四边， 则|PF1|=|FQ|，|PF|=|QF1|， 由|PF|=3|FQ|，根据椭圆的定义|PF|-|PF1|=‎2a， ∴|PF1|=a，|OP|=b，|OF1|=c， ∴∠OPF1=90°， 在△QPF1中，|PQ|=2b，|QF1|=‎3a，|PF1|=a， ∴（2b）2+a2=（‎3a）2，整理得：b2=‎2a2， 则双曲线的离心率e===． 故选：B． 由题意可知：四边形PFQF1为平行四边，利用双曲线的定义及性质，求得∠OPF1=90°，在△QPF1中，利用勾股定理即可求得a和b的关系，根据双曲线的离心率公式即可求得离心率e． 本题考查双曲线的简单几何性质简单几何性质，考查数形结合思想，属于中档题． 11.【答案】B ‎ ‎【解析】解：设△MF‎1F2的内切圆的半径等于r，则由题意可得：2πr=3π，∴r=． 由椭圆的定义可得：|MF1|+|MF2|=‎2a， 又c2=a2-b2=a2-16，∴c=， ∵满足条件的点M恰好有2个，∴M是椭圆的短轴顶点，即|yM|=4， △MF‎1F2的面积等于‎2c•|yM|=4． 又△MF‎1F2的面积等于（|MF1|+|MF2|+‎2c）r=（a+c）r=（a+）． 由（a+）=4． 解得：a2=25． 故选：B． 设△MF‎1F2的内切圆的半径等于r，由圆的周长求得r的值，由椭圆的定义可得：|MF1|+|MF2|=‎2a，然后利用△MF‎1F2的面积相等列式求得a2． 本题考查椭圆的定义、标准方程以及简单性质的应用，利用等积法是解题的关键，是中档题． 12.【答案】A ‎ ‎【解析】解：∵|F‎1F2|=2|OP|，∴PF1⊥PF2， ∴|PF1|2+|PF2|2=4（1+b2），① 由双曲线的定义可得：|PF1|-|PF2|=2，② 又tan∠PF‎2F1=≥4‎ ‎，③， 由②③得|PF2|∈（0，]，④ 由①②得（|PF2|+1）2=2b2+1，⑤ 得2b2+1∈（1，]， ∴b2+1∈（1，]， ∴离心率为∈（1，]． 故选：A． 由|F‎1F2|=2|OP|，可得PF1⊥PF2，利用勾股定理及双曲线的定义，结合tan∠PF‎2F1≥4列式求解双曲线C的离心率的取值范围． 本题考查双曲线的性质，考查双曲线定义及勾股定理的应用，考查计算能力，属中档题． 13.【答案】y2=-9x和x2= ‎ ‎【解析】解：∵点（-1，3）在第二象限， ∴满足条件的抛物线的标准方程可以是y2=-2p1x（p1＞0）或x2=2p2y（p2＞0）， 把（-1，3）代入y2=-2p1x，得p1=， 把（-1，3）代入x2=2p2y，得p2=． 因此，满足条件的抛物线有两条，它们的标准方程分别为y2=-9x和x2=． 故答案为：y2=-9x和x2=． 由点（-1，3）在第二象限，可设满足条件的抛物线的标准方程是y2=-2p1x（p1＞0）或x2=2p2y（p2＞0），分别把点的坐标代入求解p，则抛物线方程可求． 本题考查抛物线方程的求法，考查分类讨论的数学思想方法，是基础题． 14.【答案】 ‎ ‎【解析】【分析】 本题考查椭圆的简单性质的应用，考查转化思想以及计算能力，属于基础题. ​画出图形，利用椭圆的定义，以及余弦定理求出a，c的关系，然后求解椭圆的离心率即可. 【解答】 解：点P是椭圆上的一点，F1，F2分别为椭圆的左、右焦点， ∵∠F1PF2=120°，且|PF1|=3|PF2|， 如图所示： 设|PF2|=m，则|PF1|=‎3m， 则：， 可得‎4c2=13×， 解得e==． 故答案为. 15.【答案】 ‎ ‎【解析】解：∵双曲线是等轴双曲线， ∴双曲线的一条渐近线方程为x-y=0， 则x-y=0与直线x-y+1=0平行，且两平行线的距离d===， ∵点P到直线x-y=0的距离大于0， ‎ ‎∴点P到直线x-y+1=0的距离d＞， 若点P到直线x-y+1=0的距离大于m恒成立，则m≤， 即m的最大值为， 故答案为： 根据双曲线是等轴双曲线，得到渐近线方程为x-y=0，利用平行直线的距离求出两平行线的距离，结合不等式恒成立，进行转化求解即可． 本题主要考查直线和双曲线位置关系的应用，结合等轴双曲线的性质，以及平行直线的距离公式进行转化是解决本题的关键． 16.【答案】 ‎ ‎【解析】解：显然，过点A与x轴平行的直线与封闭曲线的两个交点关于点A对称，且这两个点在同一曲线上． 当对称的两个点分属两段曲线时，设其中一个点为（x1，y1），其中y1=，且-4≤x1≤4，则其关于点A的对称点为（-x1，‎2a-y1）， 所以这个点在曲线上， 所以‎2a-y1=-x12+5，即‎2a-=-x12+5， 所以‎2a=x12+5，即x12+5‎-2a=0，此方程的x1的解必须刚好有且只有两个， 当x1=4时，其对称点的横坐标刚好为-4，故x1≠±4， 于是-4＜x1＜4，且x1≠0， ∴‎2a=x12+5∈（5，8），即． 故答案为：． 由图可知过两曲线的交点的直线与x轴的交点为（0，4），所以a＜4．当对称的两个点分属两段曲线时，设其中一个点为（x1，），则其对称点为（-x1，‎2a-），将其代入曲线，得到的关于x1的方程的解有且只有两个，进而可得结果． 本题考查点的对称性、一元二次方程根的判别式，属于中档题． 17.【答案】解：由于命题p：函数f（x）=x2-ax在[0，+∞）单调递增， ∴a≤0； 命题q：方程x2+ay2=2表示焦点在y轴上的椭圆， ∴＞2，即0＜a＜1， 命题“p∨q”为真命题，“p∧q”为假命题，则p、q一真一假 ①p真q假时：，可得a≤0； ②p假q真：，可得0＜a＜1． 综上所述：a的取值范围为：a＜1． ‎ ‎【解析】由已知分别求出p，q为真命题的a的范围，再由复合命题的真假判断求解． 本题考查复合命题的真假判断，考查二次函数单调性的性质，考查椭圆的定义，是基础题． 18.【答案】解：（1）计算这100人月薪收入的样本平均数是； （2）方案一：月薪落在区间Ω左侧收活动费用约为（0.02+0.10）×400×50÷10000=0.24（万元）； 月薪落在区间Ω收活动费用约为（0.24+0.31+0.20）×600×50÷10000=2.25（万元）； 月薪落在区间Ω右侧收活动费用约为（0.09+0.04）×800×50÷10000=0.52（万元）； 因此方案一，这50人共收活动费用约为3.01（万元）， 方案二：这50人共收活动费用约为（万元）； 所以方案一能收到更多的费用． ‎ ‎【解析】（1）计算这100人月薪收入的样本平均数即可； （2）分别计算方案一、方案二中这50人共收活动费用是多少，比较得出结论． 本题考查了频率分布直方图的应用问题，是基础题． 19.【答案】解：（1）∵点在半圆上，∴，∴b=1． ∴A（-1，0），又G（0，a）， ∵点P位于点时，△AGP的面积最大， ∴OM⊥AG，∵，∴=a， ∴． 曲线C的方程为：或x2+y2=1（y≤0）． （2），设P（x0，y0），则直线PC方程为：， 令y=0，，∴ 同理：， 所以： =++8， ∵x02+y02=1，得x02=1-y02，代入上式得 =++8 =+8 =+8=4． ∴AE2+BF2为定值． ‎ ‎【解析】（1）把M点坐标代入半圆方程计算b，根据OM⊥AG计算a即可得出曲线C的方程； （2）设P（x0，y0），利用两点式方程计算E，F的坐标，从而得出AE和BF，根据x02+y02=1化简AE2+BF2即可得出结论． 本题考查了椭圆的性质，直线与圆锥曲线的关系，属于中档题． 20.【答案】解：（1）∵D()为AB的中点， ∴根据抛物线的定义知|AF|+|BF|=x1+x2+p=2x0+p， ∵|AF|+|BF|=1+2x0， ∴p=1， ∴y2=2x． （2）设直线l的方程为x=my+b， 代入抛物线方程得y2-2my-2b=0， ∵x1x2+y1y2=-1，即， ∴y1y2=-2，即y1y2=-2b=-2， ∴b=1， ∴y1+y2=‎2m，y1y2=-2， = =， ​=， ∴= ==， 令t=m2+1，t∈[1，+∞）， 则； 即的最小值为． ‎ ‎【解析】（1）根据题意，根据抛物线的定义知|AF|+|BF|=x1+x2+p，x1+x3=2x0，分析可得|AF|+|BF|=1+2x0，解可得p的值，代入抛物线的方程即可得答案； （2）设直线l的方程为x=my+b，代入抛物线方程，得y2-2my-2b=0‎ ‎，由根与系数的关系分析可得b的值，由此表示|AB|，进而可以用m表示，由函数的值域分析可得答案． 本题考查抛物线的几何性质，涉及直线与抛物线的位置关系，关键是求出抛物线的标准方程． 21.【答案】解：（Ⅰ）由题意可得，c=1，，则a=2， ∴b2=a2-c2=3， 则椭圆方程为； （Ⅱ）如图，联立，得（3+4k2）x2+8kmx+‎4m2‎-12=0． △=64k‎2m2‎-4（3+4k2）（‎4m2‎-12）=48（4k2-m2+3）， 设A（x1，y1），B（x2，y2）， 则，， ∵kOAkOB=-， ∴=， 整理得：，即‎2m2‎=4k2+3． |AB|== =． 原点O到直线kx-y+m=0的距离d=， ∴△AOB的面积S= =． ‎ ‎【解析】（Ⅰ）由题意求出c，结合离心率求得a，再由隐含条件求得b，则椭圆方程可求； （Ⅱ）联立直线方程和椭圆方程，设出A，B的坐标，利用根与系数的关系求出A，B的横纵坐标的乘积，再由kOAkOB=-得到k与m的关系，利用弦长公式求得弦长，由点到直线的距离公式求出坐标原点O到直线l的距离，代入三角形面积公式得答案． 本题考查椭圆方程的求法，考查了直线和椭圆位置关系的应用，训练了弦长公式及点到直线的距离公式的应用，是中档题． 22.【答案】解：（I）抛物线的焦点F（，0），设D（t，0），则FD的中点为（，0）． ∵|FA|=|FD|，∴3+=|t-|，解得t=3+p或t=-3（舍）． ∵，∴，解得p=2． ∴抛物线方程为y2=4x． （II）由（I）知F（1，0），设A（x0，y0），D（xD，0）， ∵|FA|=|FD|，则|xD-1|=x0+1，由xD＞0得xD=x0+2，即D（x0+2，0）． ∴直线l的斜率为kAD=-．∵l1∥l，故直线l1的斜率为-． 设直线l1的方程为y=-x+b， 联立方程组，消元得：y2+y-=0， ∵直线l1与抛物线相切， ∴△=，∴b=-． 设E（xE，yE），则yE=-，xE=， 当y02≠4时，kAE==，直线AE的方程为y-y0=（x-x0）， ∵y02=4x0，∴直线AE方程为y=．∴直线AE经过点（1，0）． 当y02=4时，直线AE方程为x=1，经过点（1，0）． 综上，直线AE过定点F（1，0）． ‎ ‎【解析】（I）根据等边三角形的性质可知A点横坐标为FD的中点横坐标，列出方程解出p． （II）根据|FA|=|FD|列出方程得出A，D横坐标的关系，从而得出l的斜率，设l1方程，与抛物线方程联立，由判别式△=0得出l的截距与A点坐标的关系，求出E 点坐标，得出AE方程，根据方程特点判断定点坐标． 本题考查了抛物线的性质，直线与抛物线的关系，属于中档题． ‎