- 2021-06-19 发布 |
- 37.5 KB |
- 25页

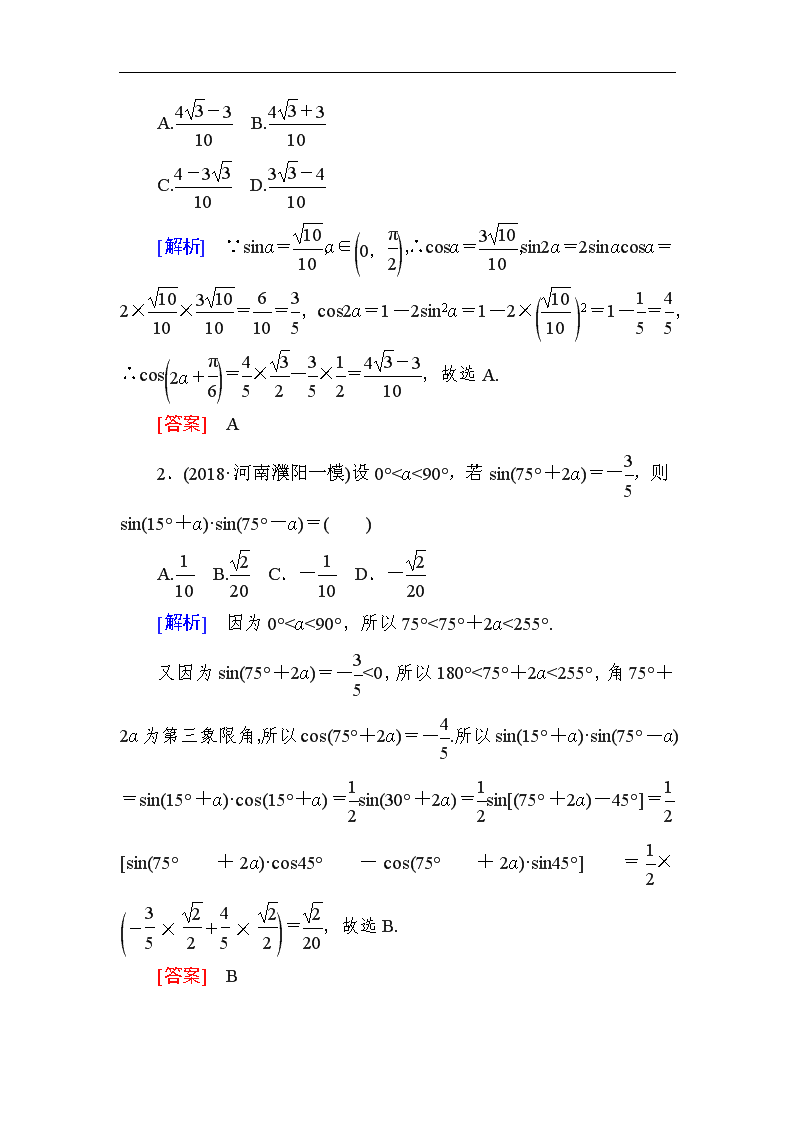

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019年高考数学精讲二轮教案第二讲三角恒等变换与解三角形
第二讲 三角恒等变换与解三角形 考点一 三角恒等变换与求值 1.两角和与差的正弦、余弦、正切公式 (1)sin(α±β)=sinαcosβ±cosαsinβ. (2)cos(α±β)=cosαcosβ∓sinαsinβ. (3)tan(α±β)=. 2.二倍角的正弦、余弦、正切公式 (1)sin2α=2sinαcosα. (2)cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α. (3)tan2α=. 3.辅助角公式 asinx+bcosx=sin(x+φ). [对点训练] 1.(2018·山西长治二模)已知sinα=,α∈,则cos的值为( ) A. B. C. D. [解析] ∵sinα=,α∈,∴cosα=,sin2α=2sinαcosα=2××==,cos2α=1-2sin2α=1-2×2=1-=,∴cos=×-×=,故选A. [答案] A 2.(2018·河南濮阳一模)设0°<α<90°,若sin(75°+2α)=-,则sin(15°+α)·sin(75°-α)=( ) A. B. C.- D.- [解析] 因为0°<α<90°,所以75°<75°+2α<255°. 又因为sin(75°+2α)=-<0,所以180°<75°+2α<255°,角75°+2α为第三象限角,所以cos(75°+2α)=-.所以sin(15°+α)·sin(75°-α)=sin(15°+α)·cos(15°+α)=sin(30°+2α)=sin[(75°+2α)-45°]=[sin(75°+2α)·cos45°-cos(75°+2α)·sin45°]=×=,故选B. [答案] B 3.(2018·豫北名校联考)计算: = ________.(用数字作答) [解析] ====. [答案] 4.(2018·河南六市联考)已知cosα=,cos(α-β)=,若0<β<α<,则β=________. [解析] 由cosα=,0<α<,得sinα===,由0<β<α<,得0<α-β<. 又cos(α-β)=, ∴sin(α-β)== =. 由β=α-(α-β)得cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)=×+×=. ∵β∈,∴β=. [答案] [快速审题] (1)看到三角函数求值,想到已知角与未知角间的和、差、倍的关系,想到公式求解. (2)看到三角函数的平方,想到用二倍角公式降幂. (1)三角恒等变换的三原则 ①一看“角”,这是最重要的一环,通过看角之间的差别与联系,把角进行合理拆分,从而正确使用公式,如2题. ②二看“函数名称”,看函数名称之间的差异,从而确定使用的公式,常见的有“切化弦”. ③三看“结构特征”,分析结构特征,可以帮助我们找到变形的方向,常见的有“遇到分式要通分”等. (2)解决条件求值应关注的三点 ①分析已知角和未知角之间的关系,正确地用已知角来表示未知角. ②正确地运用有关公式将所求角的三角函数值用已知角的三角函数值来表示. ③求解三角函数中给值求角的问题时,要根据已知求这个角的某种三角函数值,然后结合角的取值范围,求出角的大小,如4题. 考点二 解三角形 1.正弦定理 ===2R(2R为△ABC外接圆的直径). 变形:a=2RsinA,b=2RsinB,c=2RsinC. sinA=,sinB=,sinC=. a∶b∶c=sinA∶sinB∶sinC. 2.余弦定理 a2=b2+c2-2bccosA,b2=a2+c2-2accosB, c2=a2+b2-2abcosC. 推论:cosA=,cosB=, cosC=. 变形:b2+c2-a2=2bccosA,a2+c2-b2=2accosB,a2+b2-c2=2abcosC. 3.面积公式 S△ABC=bcsinA=acsinB=absinC. 角度1:利用正弦、余弦定理判断三角形的形状 [解析] 由cosB=1-2sin2得sin2=,∴=,即cosB=. 解法一:由余弦定理得=,即a2+c2-b2=2a2,∴a2+b2=c2. ∴△ABC为直角三角形,又无法判断两直角边是否相等,故选A. 解法二:由正弦定理得cosB=,又sinA=sin(B+C)=sinBcosC+cosBsinC,∴cosBsinC=sinBcosC+cosBsinC,即sinBcosC=0,又sinB≠0,∴cosC=0,又角C为三角形的内角,∴C=,∴△ABC为直角三角形,又无法判断两直角边是否相等,故选A. [答案] A 角度2:利用正弦、余弦定理进行边角计算 [解] (1)由2cosAcosC(tanAtanC-1)=1, 得2(sinAsinC-cosAcosC)=1, 即cos(A+C)=-, ∴cosB=-cos(A+C)=, 又0查看更多