专题9-5 椭 圆（讲）-2018年高考数学一轮复习讲练测（江苏版）

专题9-5 椭 圆（讲）-2018年高考数学一轮复习讲练测（江苏版）

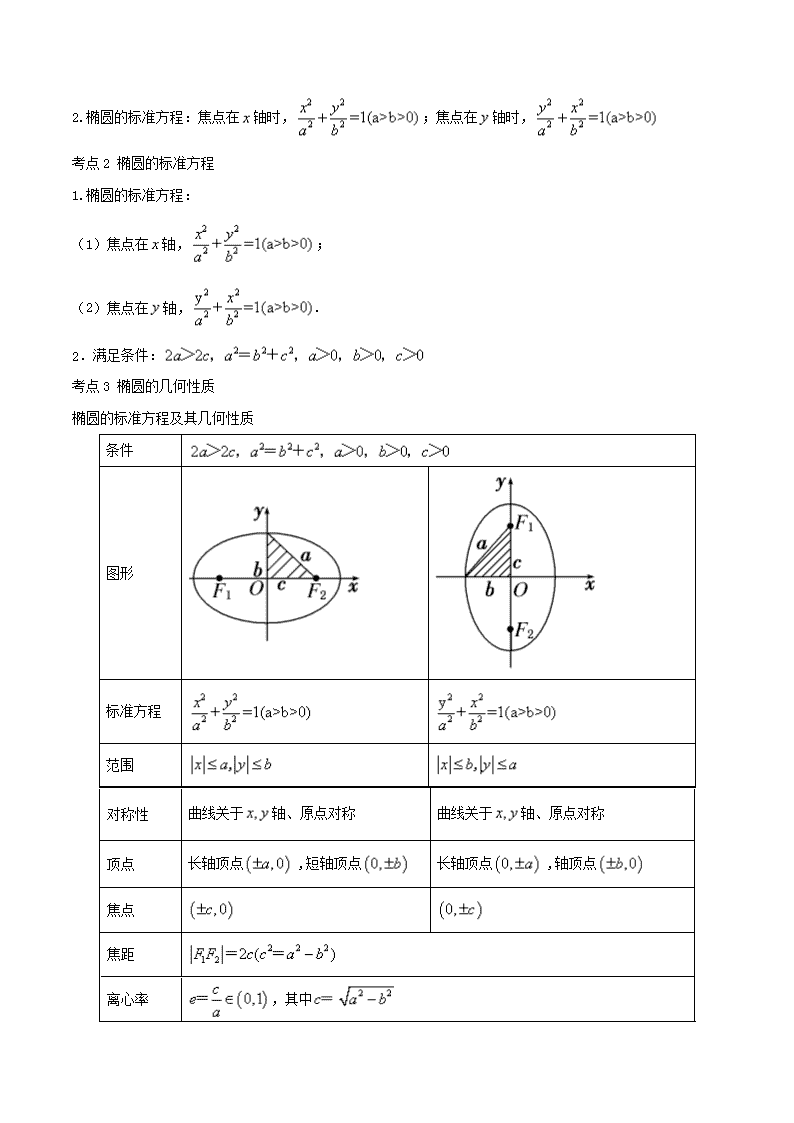
‎ ‎ ‎【考纲解读】‎ 内 容 要 求 备注 A　　‎ B　　‎ C　　‎ 圆锥曲线与方程　‎ 中心在坐标原点的椭圆的标准方程与几何性质　　‎ ‎　 　‎ ‎√　　‎ ‎　 　‎ ‎1．了解椭圆的实际背景．‎ ‎2．掌握椭圆的定义、标准方程、几何图形及简单性质．‎ ‎.‎ ‎【直击考点】‎ 题组一 常识题 ‎1． 已知△ABC的顶点B，C在椭圆＋＝1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是________．‎ ‎【解析】由椭圆定义知△ABC的周长等于椭圆长轴长的2倍，所以△ABC的周长是4×2＝8.‎ ‎2． 椭圆的中心在原点，焦点在x轴上，长轴长是短轴长的倍，焦距为4，则椭圆的标准方程为________________．‎ ‎3． 椭圆＋＝1的离心率为________．‎ ‎【解析】由＋＝1可得a2＝16，b2＝8，∴c2＝a2－b2＝8，∴e2＝＝，∴e＝.‎ 题组二　常错题 ‎4．已知条件甲：动点P到两定点A，B的距离之和为|PA|＋|PB|＝2a(a>0且a为常数)；条件乙：P点的轨迹是以A，B为焦点，且长轴长为2a的椭圆．则甲是乙的________________(填“充分不必要、必要不充分或充要”)条件．‎ ‎【解析】∵乙推出甲且甲推不出乙，∴甲是乙的必要不充分条件．‎ ‎5．已知椭圆的焦点在坐标轴上，中心在坐标原点，若直线x－2y＋2＝0经过该椭圆的一个焦点和一个顶点，则该椭圆的标准方程为__________________________．‎ ‎【解析】易知直线与坐标轴的交点为(0，1)，(－2，0)，由题意知当焦点在x轴上时，c＝2，b＝1，∴a2＝5，所求椭圆的标准方程为＋y2＝1.‎ 当焦点在y轴上时，b＝2，c＝1，∴a2＝5，所求椭圆的标准方程为＋＝1.‎ 题组三　常考题 ‎6． 已知椭圆＋＝1(a>b>0)的右焦点为F(4，0)，短轴长为6，则a＝________．‎ ‎【解析】依题意2b＝6，所以b＝3，又c＝4，所以a＝＝5.‎ ‎7． 直线l经过椭圆的两个相邻顶点，若椭圆中心到l的距离为其长轴长的，则该椭圆的离心率为 __________．‎ ‎8． 已知圆Q：(x－1)＋y2＝16，动圆M过定点P(－1，0)且与圆Q相切，则圆心M的轨迹方程是________________．‎ ‎【解析】点P(－1，0)在圆Q内，故圆M与圆Q内切．设M(x，y)，圆M的半径为r，则|MQ|＝4－r.又圆M过定点P(－1，0)，所以|MP|＝r，所以|MQ|＝4－|MP|，即|MQ|＋|MP|＝4.由椭圆定义知，圆心M的轨迹是椭圆，且c＝1，a＝2，所以b＝，所以椭圆方程为＋＝1.‎ ‎【知识清单】‎ 考点1 椭圆的定义及其应用 ‎1.椭圆的概念 ‎(1)文字形式：在平面内到两定点F1、F2的距离的和等于常数(大于|F‎1F2|)的点的轨迹(或集合)叫椭圆．这两定点叫做椭圆的焦点 ，两焦点间的距离叫做焦距．‎ ‎(2)代数式形式：集合 ‎①若，则集合P为椭圆；‎ ‎②若，则集合P为线段；‎ ‎③若，则集合P为空集．‎ ‎2.椭圆的标准方程：焦点在轴时，；焦点在轴时，‎ 考点2 椭圆的标准方程 ‎1.椭圆的标准方程：‎ ‎（1）焦点在轴，；‎ ‎（2）焦点在轴，.‎ ‎2．满足条件：‎ 考点3 椭圆的几何性质 椭圆的标准方程及其几何性质 条件 图形 标准方程 范围 对称性 曲线关于轴、原点对称 曲线关于轴、原点对称 顶点 长轴顶点 ,短轴顶点 长轴顶点 ,轴顶点 焦点 焦距 离心率 ‎，其中 通径 过焦点垂直于长轴的弦叫通径，其长为 考点4 直线与椭圆的位置关系 ‎1.直线与椭圆位置关系的判断 ‎(1)代数法：把椭圆方程与直线方程联立消去y，整理得到关于x的方程Ax2＋Bx＋C＝0.记该一元二次方程根的判别式为Δ，①若Δ＞0，则直线与椭圆相交；②若Δ＝0，则直线与椭圆相切；③若Δ＜0，则直线与椭圆相离．‎ ‎(2)几何法：在同一直角坐标系中画出椭圆和直线，利用图象和性质可判断直线与椭圆的位置关系．‎ ‎2．直线与椭圆的相交长问题：‎ ‎（1）弦长公式：设直线与椭圆有两个公共点则弦长公式为或．‎ ‎（2）弦中点问题，适用“点差法”.‎ ‎【考点深度剖析】‎ ‎ 椭圆是圆锥曲线中最重要的一类曲线，在高考中出现的次数也最多，主要考查椭圆的定义、性质、方程，在解答题中多与直线、向量、轨迹等综合出题．‎ ‎【重点难点突破】‎ 考点1 椭圆的定义及其应用 ‎【1-1】[2015·扬州模拟]已知椭圆的焦点是F1、F2，P是椭圆的一个动点，如果M是线段F1P的中点，那么动点M的轨迹是________．‎ ‎【答案】椭圆 ‎【1-2】已知F1、F2是椭圆C：＋＝1(a>b>0)的两个焦点，P为椭圆C上的一点，且⊥.若△PF‎1F2的面积为9，则b＝________.‎ ‎【答案】3‎ ‎【思想方法】‎ ‎1. 涉及到动点到两定点距离之和为常数的问题，可直接用椭圆定义求解．‎ ‎2.涉及椭圆上点、焦点构成的三角形问题，往往利用椭圆定义、勾股定理或余弦定理求解.‎ ‎【温馨提醒】应用椭圆的定义，可以得到结论：（1）椭圆上任意一点P(x，y)(y≠0)与两焦点F1(－c,0)，F2(c,0)构成的△PF‎1F2称为焦点三角形，其周长为2(a＋c)．‎ ‎(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形，其中a是斜边，a2＝b2＋c2.‎ 考点2 椭圆的标准方程 ‎【2-1】【2014年全国普通高等学校招生统一考试文科数学（大纲卷）】已知椭圆C：的左右焦点为F1,F2离心率为，过F2的直线l交C与A,B两点，若△AF1B的周长为，则C的方程为________．‎ ‎【答案】‎ ‎【解析】由椭圆的定义可得，又因为,所以，解得，又因为，所以， ，所以椭圆方程为. ‎ ‎【2-2】求满足下列各条件的椭圆的标准方程：‎ ‎(1)长轴是短轴的3倍且经过点；‎ ‎(2)短轴一个端点与两焦点组成一个正三角形，且焦点到同侧顶点的距离为；‎ ‎【答案】 (1) 或　(2) ，或　‎ ‎【思想方法】‎ ‎1．求椭圆标准方程的方法 求椭圆的标准方程，除了直接根据定义外，常用待定系数法(先定性，后定型，再定参)．‎ 当椭圆的焦点位置不明确而无法确定其标准方程时，可设方程为 ，可以避免讨论和繁杂的计算，也可以设为 (A＞0，B＞0且A≠B)，这种形式在解题中更简便．‎ ‎2．椭圆的标准方程有两种形式，其结构简单，形式对称且系数的几何意义明确，在解题时要防止遗漏，要深刻理解椭圆中的几何量等之间的关系，并能熟练地应用．‎ ‎【温馨提醒】1.用待定系数法求椭圆标准方程的一般步骤是：‎ ‎(1)作判断：根据条件判断焦点的位置．‎ ‎(2)设方程：焦点不确定时，要注意分类讨论，或设方程为 ．‎ ‎(3)找关系：根据已知条件，建立关于的方程组．‎ ‎(4)求解，得方程．‎ ‎2．(1)方程与有相同的离心率．‎ ‎(2)与椭圆共焦点的椭圆系方程为，恰当运用椭圆系方程，可使运算简便．‎ 考点3 椭圆的几何性质 ‎【3-1】【2014年全国普通高等学校招生统一考试理科数学（大纲卷）】已知椭圆C：的左、右焦点为、，离心率为，过的直线交C于A、B两点，若的周长为，则C的方程为________．‎ ‎【答案】‎ ‎【3-2】设是椭圆上一点，是椭圆的两个焦点，________．‎ ‎【答案】‎ ‎【解析】由椭圆方程可知，即，。因为，所以，所以，因为，解得.因为，所以.‎ ‎【思想方法】‎ ‎1.在求解有关离心率的问题时，一般并不是直接求出c和a的值，而是根据题目给出的椭圆的几何特征，建立关于参数c、a、b的方程或不等式，通过解方程或不等式求得离心率的值或范围．较多时候利用解题； ‎ ‎2.对焦点三角形的处理方法，通常是运用.‎ ‎【温馨提醒】1.学习中，要注意椭圆几何性质的挖掘：‎ ‎(1)椭圆中有两条对称轴，“六点”(两个焦点、四个顶点)，要注意它们之间的位置关系(如焦点在长轴上等)以及相互间的距离(如焦点到相应顶点的距离为a－c)，过焦点垂直于长轴的通径长为等．‎ ‎(2)设椭圆上任意一点P(x，y)，则当x＝0时，|OP|有最小值b，这时，P在短轴端点处；当x＝a时，|OP|有最大值a，这时P在长轴端点处．‎ ‎(3)椭圆上任意一点P(x，y)(y≠0)与两焦点F1(－c,0)，F2(c,0)构成的△PF‎1F2称为焦点三角形，其周长为2(a＋c)．‎ ‎(4)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形，其中a是斜边，a2＝b2＋c2.‎ ‎2．重视向量在解析几何中的应用，注意合理运用中点、对称、弦长、垂直等几何特征．‎ 考点4 直线与椭圆的位置关系 ‎【4-1】过椭圆左焦点F斜率为1的直线交椭圆于A，B两点，向量与向量共线，则该椭圆的离心率为________．‎ ‎【答案】‎ ‎【4-2】【2014年全国普通高等学校招生统一考试理科数学（江西卷）】过点作斜率为的直线与椭圆：相交于，若是线段的中点，则椭圆的离心率为 ‎ ‎【答案】‎ ‎【解析】设，则由两式相减变形得：即，从而 ‎【思想方法】‎ ‎1.涉及直线与椭圆的基本题型有：‎ ‎（1）位置关系的判断 ‎（2）弦长、弦中点问题 ‎（3）轨迹问题 ‎（4）定值、最值及参数范围问题 ‎（5）存在性问题 ‎2．常用思想方法和技巧有：‎ ‎（1）设而不求（2）坐标法（3）根与系数关系 ‎3. 若直线与椭圆有两个公共点可结合韦达定理，代入弦长公式或，求距离．‎ ‎【温馨提醒】1.涉及直线与椭圆的基本题型有：‎ ‎（1）位置关系的判断 ‎（2）弦长、弦中点问题 ‎（3）轨迹问题 ‎（4）定值、最值及参数范围问题 ‎（5）存在性问题 ‎2．常用思想方法和技巧有：（1）数形结合思想；（2）设而不求；（3）坐标法；（4）根与系数关系.‎ ‎【易错试题常警惕】‎ ‎[失误与防范]‎ ‎1．判断两种标准方程的方法为比较标准形式中x2与y2的分母大小．‎ ‎2．注意椭圆的范围，在设椭圆＋＝1 (a>b>0)上点的坐标为P(x，y)时，则|x|≤a，这往往在求与点P有关的最值问题中用到，也是容易被忽略而导致求最值错误的原因．‎