人教新课标A版高二数学选修2-1综合测试题(基础)

人教新课标A版高二数学选修2-1综合测试题(基础)

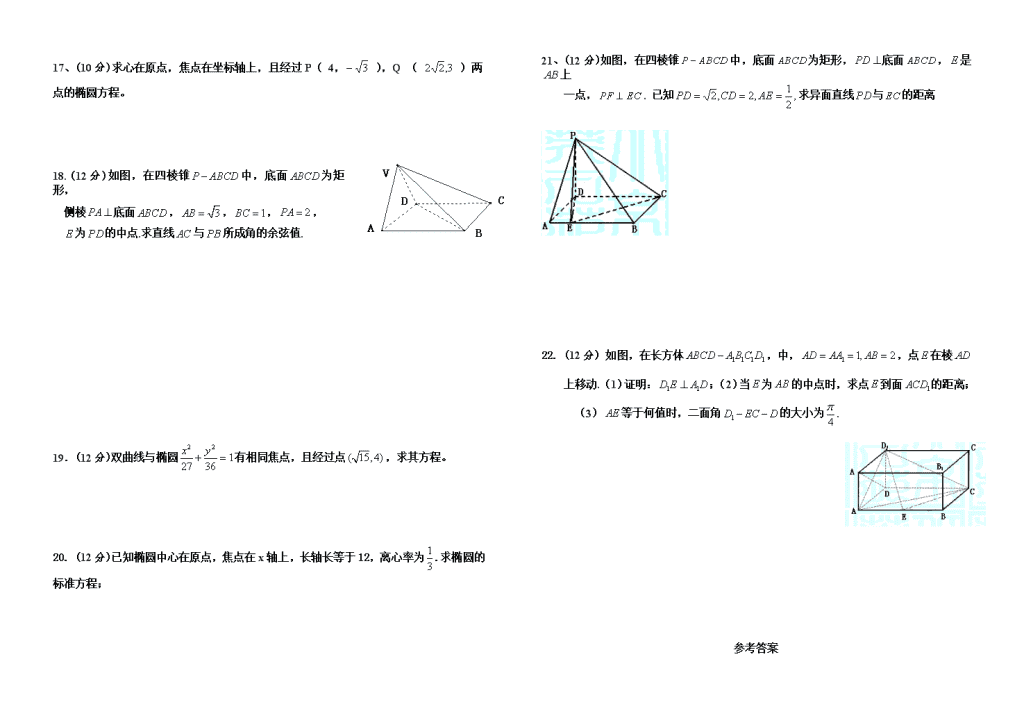
高二级数学（理科）测试卷题 班级 姓名 座号 成绩 一、选择题（本题包括 12 个小题，每小题 5 分，共计 60 分） 1.命题 P ：“ a R  ，则 2 0a  ”,则 P 为 A. a R  ， 2 0a  B. a R  ， 2 0a  C. a R  ， 2 0a  D. a R  ， 2 0a  2.双曲线 2 2 19 16 x y  的渐近线方程 A. xy 4 3 B. xy 3 4 C. 16 9y x  D. 9 16y x  3.抛物线 2 8y x 的准线方程是 A． 2y B． 2y C． 2x  D．． 2x   4. 原命题“若 2a b  ，则 ,a b 中至少有一个不小于1”，则原命题与其逆命题 的真假情况是 A．原命题与逆命题均为假命题 B．原命题为假命题，逆命题为真命题 C．原命题与逆命题均为真命题 D．原命题为真命题，逆命题为假命题 5.焦点在 x 轴上,虚轴长为 12，离心率为 4 5 的双曲线标准方程是 A． 2 2 164 144 x y  B 2 2 136 64 x y  ．C. 2 2 164 16 y x  D 2 2 164 36 x y  . 6.椭圆 2 2 14 5 x y+ = 的一个焦点坐标是 A.（3，0） B.（0，3） C.（1，0） D.（0，1） 7．已知点 ( 3,1, 4)A   ，则点 A 关于 x 轴对称的点的坐标为（ ） A． )4,1,3(  B． )4,1,3(  C． )4,1,3( D． )4,1,3(  8.若命题“ 2, ( 1) 1 0x R x a x     使 ”是假命题，则实数a 的取值范围为 A．1 3a  B． 1 1a   C． 3 3a   D． 1 3a   9.设点 A 为双曲线 2 2 112 4 x y- = 的右顶点，则点 A 到该双曲线的一条渐近线的距离是 A. 3 B.3 C. 3 2 D. 3 2 10. 若向量 )2,1,2(),2,,1(  ba   ，且 a 与b  的夹角余弦为 9 8 ，则 等于（ ） A． 2 B． 2 C． 2 或 55 2 D． 2 或 55 2 11.椭圆 2 2 2 2 1x y a b   （ 0a b  ）的两焦点分别为 1F 、 2F ，以 1F 2F 为边作正三角形，若 正三角形的第三个顶点恰好是椭圆短轴的一个端点，则椭圆的离心率为 A. 1 2 B. 3 2 C. 2 2 D. 3 3 12．过点 (0,1)P 与抛物线 2y x 有且只有一个交点的直线有 A.4 条 B.3 条 C.2 条 D.1 条 二、填空题（本题包括 4 个小题，每小题 5 分，共计 20 分） 13、椭圆 11625 22  yx 上的一点 P 到椭圆一个焦点的距离为3，则 P 到另一焦点距离为 14、 : 6A x  , 2: 4 5 0B x x   , 则 A 是 B 的___________条件 15．若( 3 )a b  )57( ba   ，且( 4 )a b  )57( ba   ，则 a 与b  的夹角为___________。 16．若 19(0,2, )8A ， 5(1, 1, )8B  ， 5( 2,1, )8C  是平面 内的三点，设平面 的法向量 ),,( zyxa  ， 则 zyx :: ________________。 三、解答题（本题包括 6 个小题，共计 70 分） 17、(10 分)求心在原点，焦点在坐标轴上，且经过 P（ 4， 3 ），Q （ 3,22 ）两 点的椭圆方程。 18. (12 分)如图，在四棱锥 P ABCD 中，底面 ABCD 为矩形， 侧棱 PA  底面 ABCD ， 3AB  ， 1BC  ， 2PA  ， E 为 PD 的中点.求直线 AC 与 PB 所成角的余弦值. 19．(12 分)双曲线与椭圆 13627 22  yx 有相同焦点，且经过点( 15,4) ，求其方程。 20. (12 分)已知椭圆中心在原点，焦点在 x 轴上，长轴长等于 12，离心率为 1 3 .求椭圆的 标准方程； 21、(12 分)如图，在四棱锥 P ABCD 中，底面 ABCD 为矩形，PD  底面 ABCD ，E 是 AB 上 一点， PF EC . 已知 ,2 1,2,2  AECDPD 求异面直线 PD 与 EC 的距离 22. (12 分) 如图，在长方体 1 1 1 1ABCD A B C D ，中， 1 1, 2AD AA AB   ，点 E 在棱 AD 上移动.（1）证明： 1 1D E A D ；（2）当 E 为 AB 的中点时，求点 E 到面 1ACD 的距离； （3） AE 等于何值时，二面角 1D EC D  的大小为 4  . 参考答案 D C B A V 1.命题 P ：“ a R  ，则 2 0a  ”,则 P 为 C A. a R  ， 2 0a  B. a R  ， 2 0a  C. a R  ， 2 0a  D. a R  ， 2 0a  2.双曲线 2 2 19 16 x y  的渐近线方程是 B A. xy 4 3 B. xy 3 4 C. 16 9y x  D. 9 16y x  3.抛物线 2 8y x 的准线方程是 D A． 2y B． 2y C． 2x  D．． 2x   4. 原命题“若 2a b  ，则 ,a b 中至少有一个不小于1”，则原命题与其逆命题 的真假情况是 D A．原命题与逆命题均为假命题 B．原命题为假命题，逆命题为真命题 C．原命题与逆命题均为真命题 D．原命题为真命题，逆命题为假命题 5.焦点在 x 轴上,虚轴长为 12，离心率为 4 5 的双曲线标准方程是 D A． 2 2 164 144 x y  B 2 2 136 64 x y  ． C. 2 2 164 16 y x  D 2 2 164 36 x y  . 6.椭圆 2 2 14 5 x y+ = 的一个焦点坐标是（ D ） A.（3，0） B.（0，3） C.（1，0） D.（0，1） 7．已知点 ( 3,1, 4)A   ，则点 A 关于 x 轴对称的点的坐标为（ A ） A． )4,1,3(  B． )4,1,3(  C． )4,1,3( D． )4,1,3(  8.若命题“ 2, ( 1) 1 0x R x a x     使 ”是假命题，则实数 a的取值范围为 D A．1 3a  B． 1 1a   C． 3 3a   D． 1 3a   9.设点 A 为双曲线 2 2 112 4 x y- = 的右顶点，则点 A 到该双曲线的一条渐近线的距离是 （ A ） A. 3 B.3 C. 3 2 D. 3 2 10. 若向量 )2,1,2(),2,,1(  ba   ，且 a 与b  的夹角余弦为 9 8 ，则 等于（ C ） A． 2 B． 2 C． 2 或 55 2 D． 2 或 55 2 11.椭圆 2 2 2 2 1x y a b   （ 0a b  ）的两焦点分别为 1F 、 2F ，以 1F 2F 为边作正三角形，若 正三角形的第三个顶点恰好是椭圆短轴的一个端点，则椭圆的离心率为 A A. 1 2 B. 3 2 C. 2 2 D. 3 3 12．过点 (0,1)P 与抛物线 2y x 有且只有一个交点的直线有（ B ） A.4 条 B.3 条 C.2 条 D.1 条 13、已知椭圆 11625 22  yx 上的一点 P 到椭圆一个焦点的距离为3，则 P 到另一焦点距离为 7 14、 : 6A x  , 2: 4 5 0B x x   , 则 A 是 B 的___________条件 15．若( 3 )a b  )57( ba   ，且( 4 )a b  )57( ba   ，则 a 与b  的夹角为____0________。 16．若 19(0,2, )8A ， 5(1, 1, )8B  ， 5( 2,1, )8C  是平面 内的三点，设平面 的法向量 ),,( zyxa  ， 则 zyx :: ________ 2:3:( 4) ________。 17、求心在原点，焦点在坐标轴上，且经过 P（ 4， 3 ），Q （ 3,22 ）两点的椭 圆方程。 解：设椭圆方程为 12 2 2 2  b y a x ，将 P，Q 两点坐标代入，解得 15,20 22  ba 故 11520 22  yx 为所求。 18. 如图，在四棱锥 P ABCD 中，底面 ABCD 为矩形， 侧棱 PA  底面 ABCD ， 3AB  ， 1BC  ， 2PA  ， E 为 PD 的中点. （Ⅰ）求直线 AC 与 PB 所成角的余弦值； 解：（Ⅰ）建立如图所示的空间直角坐标系， 则 , , , , ,A B C D P E 的坐标为 (0,0,0)A 、 ( 3,0,0)B 、 ( 3,1,0)C 、 (0,1,0)D 、 (0,0,2)P 、 1(0, ,1)2E ， 从而 ).2,0,3(),0,1,3(  PBAC 设 PBAC与 的夹角为 ，则 ,14 73 72 3 |||| cos    PBAC PBAC ∴ AC 与 PB 所成角的余弦值为 14 73 . 19．双曲线与椭圆 13627 22  yx 有相同焦点，且经过点( 15,4) ，求其方程。 解：椭圆 2 2 136 27 y x  的焦点为(0, 3), 3c  ，设双曲线方程为 2 2 2 2 19 y x a a   过点 ( 15,4) ，则 2 2 16 15 19a a   ，得 2 4, 36a  或 ，而 2 9a  ， 2 4a  ，双曲线方程为 2 2 14 5 y x  。 20.(本小题满分 8 分) 已知椭圆中心在原点，焦点在 x 轴上，长轴长等于 12，离心率为 1 3 . 求椭圆的标准方程； 解：设椭圆的半长轴长为 a，半短轴长为 b，半焦距为 c. 由已知，2a＝12，所以 a＝ 6. （1 分） 又 1 3 c a = ，即 a＝3c，所以 3c＝6，即 c＝2. （2 分） 于是 b2＝a2－c2＝36－4＝32. （3 分） 因为椭圆的焦点在 x 轴上，故椭圆的标准方程是 2 2 136 32 x y+ = 21、如图，在四棱锥 P ABCD 中，底面 ABCD 为矩形， PD  底面 ABCD ， E 是 AB 上 一点， PF EC . 已知 ,2 1,2,2  AECDPD 求（Ⅰ）异面直线 PD 与 EC 的距离； 解：（Ⅰ）以 D 为原点， DA 、 DC 、 DP 分别为 , ,x y z 轴建立空间直角坐标系. 由已知可得 (0,0,0), (0,0, 2), (0,2,0)D P C 设 ),0,2,(),0)(0,0,( xBxxA 则 ).0,2 3,(),2,2 1,(),0,2 1,(  xCExPExE 由 0 CEPECEPE 得 ， 即 .2 3,04 32  xx 故 由 CEDECEDE  得0)0,2 3,2 3()0,2 1,2 3( ， 又 PD DE ，故 DE 是异面直线 PD 与CE 的公垂线，易得 1|| DE ，故异面直线 PD ,CE 的距离为1. 22. 如图，在长方体 1 1 1 1ABCD A B C D ，中， 1 1, 2AD AA AB   ，点 E 在棱 AD 上移动. （1）证明： 1 1D E A D ； （2）当 E 为 AB 的中点时，求点 E 到面 1ACD 的距离； （3） AE 等于何值时，二面角 1D EC D  的大小为 4  . 解：以 D 为坐标原点，直线 1, ,DA DC DD 分别为 , ,x y z 轴，建立空间直角坐标系，设 AE x ，则 1 1(1,0,1), (0,0,1), (1, ,0), (1,0,0), (0,2,0)A D E x A C D C B A V （1） .,0)1,,1(),1,0,1(, 1111 EDDAxEDDA  所以因为 （2）因为 E 为 AB 的中点，则 (1,1,0)E ，从而 )0,2,1(),1,1,1(1  ACED ， )1,0,1(1 AD ，设平面 1ACD 的法向量为 ),,( cban  ，则      ,0 ,0 1ADn ACn 也即      0 02 ca ba ，得      ca ba 2 ，从而 )2,1,2(n ，所以点 E 到平面 1ACD 的距离为 .3 1 3 212 || || 1  n nEDh （3）设平面 1D EC 的法向量 ),,( cban  ，∴ ),1,0,0(),1,2,0(),0,2,1( 11  DDCDxCE 由           .0)2( 02 ,0 ,01 xba cb CEn CDn 令 1, 2, 2b c a x     ， ∴ ).2,1,2( xn  依题意 .2 2 5)2( 2 2 2 |||| || 4cos 2 1 1      xDDn DDn ∴ 321 x （不合，舍去）， 322 x . ∴ 2 3AE   时，二面角 1D EC D  的大小为 4  .