2021高三数学人教B版一轮学案：第八章 第一节　直线的倾斜角与斜率、直线方程

2021高三数学人教B版一轮学案：第八章 第一节　直线的倾斜角与斜率、直线方程

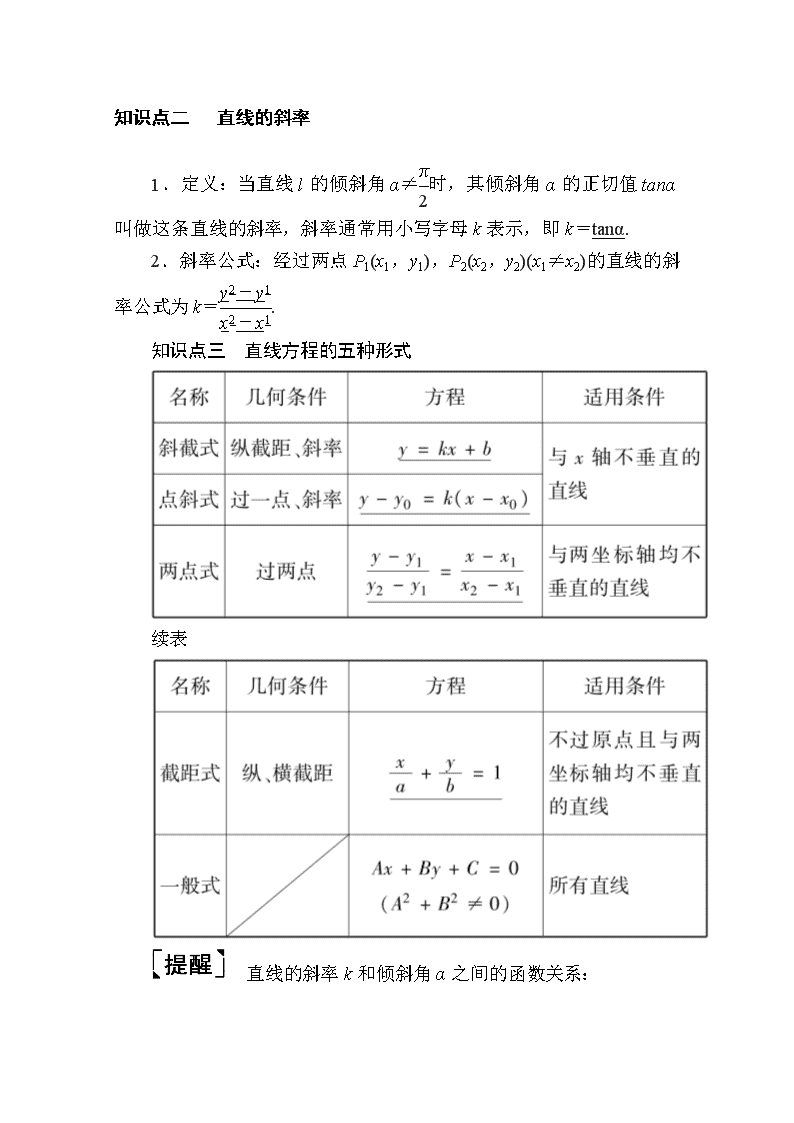
www.ks5u.com ‎　　　　　　　　第八章 平面解析几何 第一节　直线的倾斜角与斜率、直线方程 最新考纲 考情分析 ‎1.理解直线的倾斜角和斜率的概念，掌握过两点的直线斜率的计算公式．‎ ‎2．掌握确定直线位置的几何要素．‎ ‎3．掌握直线方程的几种形式(点斜式、两点式及一般式等)，了解斜截式与一次函数的关系．‎ ‎1.高考对本节的考查主要涉及直线方程的求法，两直线的平行与垂直的判定或由两直线平行与垂直求参数值或参数的取值范围．‎ ‎2．常与向量、圆锥曲线(椭圆、双曲线、抛物线)的几何性质、位置关系相结合考查，有时也会命制新定义问题．‎ ‎3．题型以选择题、填空题为主，属中低档题.‎ ‎　　　　　　　　　　　　　　　　‎ 知识点一 直线的倾斜角 ‎1．定义：当直线l与x轴相交时，我们取x轴作为基准，x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角．‎ ‎2．规定：当直线l与x轴平行或重合时，规定它的倾斜为0.‎ ‎3．范围：直线的倾斜角α的取值范围是[0，π)．‎ 知识点二 直线的斜率 ‎1．定义：当直线l的倾斜角α≠时，其倾斜角α的正切值tanα叫做这条直线的斜率，斜率通常用小写字母k表示，即k＝tanα.‎ ‎2．斜率公式：经过两点P1(x1，y1)，P2(x2，y2)(x1≠x2)的直线的斜率公式为k＝.‎ 知识点三 直线方程的五种形式 续表 直线的斜率k和倾斜角α之间的函数关系：‎ ‎1．思考辨析 判断下列结论正误(在括号内打“√”或“×”)‎ ‎(1)直线的倾斜角越大，其斜率就越大．(　×　)‎ ‎(2)直线的斜率为tanα，则其倾斜角为α.(　×　)‎ ‎(3)斜率相等的两直线的倾斜角不一定相等．(　×　)‎ ‎(4)经过任意两个不同的点P1(x1，y1)，P2(x2，y2)的直线都可以用方程(y－y1)(x2－x1)＝(x－x1)(y2－y1)表示．(　√　)‎ 解析：(1)当直线的倾斜角α1＝135°，α2＝45°时，α1>α2，但其对应斜率k1＝－1，k2＝1，k10，b>0，直线l的方程为＋＝1，所以＋＝1.‎ ‎||·||＝－·＝－(a－2，－1)·(－2，b－1)＝2(a－2)＋b－1＝‎2a＋b－5‎ ‎＝(‎2a＋b)－5＝＋≥4，‎ 当且仅当a＝b＝3时取等号，此时直线l的方程为x＋y－3＝0.‎ 方法技巧 与直线方程有关问题的常见类型及解题策略 (1)求解与直线方程有关的最值问题.先设出直线方程，建立目标函数，再利用基本不等式求解最值.‎ (2)求直线方程.弄清确定直线的两个条件，由直线方程的几种特殊形式直接写出方程.‎ (3)求参数值或范围.注意点在直线上，则点的坐标适合直线的方程，再结合函数的性质或基本不等式求解.‎ ‎1．若直线ax＋by＝ab(a>0，b>0)过点(1,1)，则该直线在x轴，y轴上的截距之和的最小值为(　C　)‎ A．1 B．2‎ C．4 D．8‎ 解析：∵直线ax＋by＝ab(a>0，b>0)过点(1,1)，‎ ‎∴a＋b＝ab，即＋＝1，‎ ‎∴a＋b＝(a＋b) ‎＝2＋＋≥2＋2＝4，‎ 当且仅当a＝b＝2时上式等号成立．‎ ‎∴直线在x轴，y轴上的截距之和的最小值为4.‎ ‎2．已知直线l：x－my＋m＝0上存在点M满足与A(－1,0)，B(1,0)两点连线的斜率kMA与kMB之积为3，则实数m的取值范围是(　C　)‎ A．[－，]‎ B．∪ C．∪ D． 解析：设M(x，y)，由kMA·kMB＝3，得·＝3，即y2＝3x2－3.联立 得x2＋x＋6＝0(m≠0)，则Δ＝2－24≥0，即m2≥，解得m≤－或m≥.‎ ‎∴实数m的取值范围是∪.‎ ‎　　　　　　　　　　　　　　　　 ‎ ‎【典例】　设直线l的方程为(a＋1)x＋y＋2－a＝0(a∈R)．‎ ‎(1)若l在两坐标轴上的截距相等，求直线l的方程；‎ ‎(2)若l在两坐标轴上的截距互为相反数，求a.‎ ‎【错解展示】　(1)令x＝0得y＝a－2，‎ 令y＝0得x＝，∴＝a－2，∴a＋1＝1，‎ ‎∴a＝0.‎ ‎∴直线l的方程为x＋y＋2＝0.‎ ‎(2)令＝－(a－2)，‎ ‎∴a＋1＝－1，∴a＝－2.‎ ‎【现场纠错】　(1)当直线过原点时，该直线在x轴和y轴上的截距为0，∴a＝2，方程即为3x＋y＝0.‎ 当直线不经过原点时，截距存在且均不为0，‎ 直线方程可写为＋＝1，‎ ‎∴＝a－2，即a＋1＝1.‎ ‎∴a＝0，方程即为x＋y＋2＝0.‎ 综上，直线l的方程为3x＋y＝0或x＋y＋2＝0.‎ ‎(2)由＝－(a－2)，得a－2＝0或a＋1＝－1，‎ ‎∴a＝2或a＝－2.‎ ‎【纠错心得】　在求与截距有关的直线方程时，注意对直线的截距是否为零进行分类讨论，防止忽视截距为零的情形，导致产生漏解．‎