中考数学专题复习圆压轴八大模型题5三切线组合

中考数学专题复习圆压轴八大模型题5三切线组合

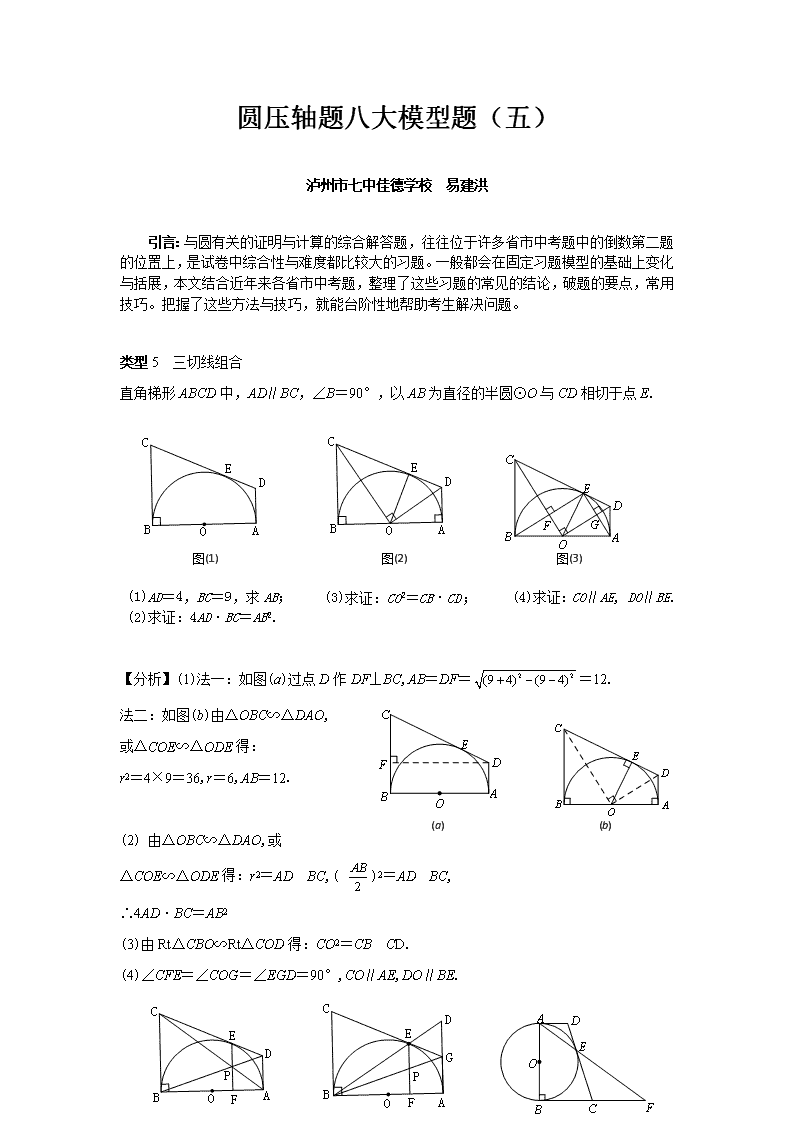
圆压轴题八大模型题（五）‎ 泸州市七中佳德学校 易建洪 ‎ 引言：与圆有关的证明与计算的综合解答题，往往位于许多省市中考题中的倒数第二题的位置上，是试卷中综合性与难度都比较大的习题。一般都会在固定习题模型的基础上变化与括展，本文结合近年来各省市中考题，整理了这些习题的常见的结论，破题的要点，常用技巧。把握了这些方法与技巧，就能台阶性地帮助考生解决问题。‎ 类型5 三切线组合 直角梯形ABCD中，AD∥BC，∠B＝90°，以AB为直径的半圆⊙O与CD相切于点E.‎ ‎ ‎ 图(2)‎ 图(3)‎ 图(1)‎ ‎(4)求证：CO∥AE, DO∥BE.‎ ‎(3)求证：CO2＝CB·CD；‎ ‎(1)AD＝4，BC＝9，求AB；‎ ‎(2)求证：4AD·BC＝AB2.‎ ‎【分析】(1)法一：如图(a)过点D作DF⊥BC,AB＝DF＝＝12.‎ 法二：如图(b)由△OBC∽△DAO,‎ 或△COE∽△ODE得：‎ r2＝4×9＝36,r＝6,AB＝12.‎ ‎(a)‎ ‎(b)‎ ‎(2) 由△OBC∽△DAO,或 ‎△COE∽△ODE得：r2＝AD×BC,( )2＝AD×BC,‎ ‎∴4AD·BC＝AB2‎ ‎(3)由Rt△CBO∽Rt△COD得：CO2＝CB×CD.‎ ‎(4)∠CFE＝∠COG＝∠EGD＝90°,CO∥AE,DO∥BE.‎ ‎ ‎ 图(6)‎ 图(5)‎ 图(4)‎ ‎(6)求证：DG=AG.‎ ‎(7)求证：EP=FP.‎ ‎(5)求证：EP=FP.‎ ‎(8)若AB=2，AD=2，求BC和EF的长.‎ ‎【分析】(5)由CB∥EF∥DA,CB＝CE,DA＝DE得,∴EP＝FP.‎ ‎(6)由CB＝CE,∠CBE＝∠CEB＝∠DEG;CB∥DA得∠CBE＝∠D,∴∠DEG＝∠D.∴DG＝EG,又EG＝GA,∴DG＝AG.‎ ‎(7)EF∥DA,得, 又DG＝GA,得EP＝FP.‎ ‎(8)由AB2＝4AD×BC得：（2）2＝4×2BC,∴BC＝2.5,CF＝BC＝2.5,BF＝5.‎ 在Rt△ABF中，AF＝＝3.由AD∥BF得,‎ ‎∴EF＝AF＝×3＝‎ ‎【典例】‎ ‎（2018·湖南娄底）如图，已知半圆O与四边形ABCD的边AD、AB、BC都相切，切点分别为D、E、C，半径OC＝1，则AE·BE___________.‎ 图a 图5-1‎ ‎【分析】连接 OE，由切线长定理可得∠AOE＝∠DOE，∠BOE＝∠EOC，再根据∠DOE＋∠EOC＝180°，可得∠AOB＝90°，继而可证△AEO∽△OEB，根据相似三角形对应边成比例即可得.‎ 解：如图，连接 OE，∵AD、AB与半圆 O 相切，‎ ‎∴ OE⊥AB，OA平分∠DOE，‎ ‎∴∠AOE＝∠DOE，同理∠BOE＝∠EOC，‎ ‎∵∠DOE＋∠EOC＝180°，∴∠AOE＋∠BOE＝90°，‎ 即∠AOB＝90°，∴∠ABO＋∠BAO＝90°，‎ ‎∵∠BAO＋∠AOE＝90°，∴∠ABO＝∠AOE，‎ ‎∵∠OEA＝∠BEO＝90°，∴△AEO∽△OEB，‎ ‎∴AE：OE＝OE：BE，∴AE•BE＝OE²＝1，‎ 答案：1.‎ ‎【点拨】‎ 由切线长定理引出的四个母子相似三角形中，含直角三角形、等腰三角形、全等三角形及相似三角形。除开由切线长所在的特殊四边形的特殊结论以外，往往借助切线长定理中的边等角等和比例线段证明线段相等，或运用局部占总体的比例求线段长。善于分解图形，构建基本的图形模型，综合运用解决问题。‎ ‎【变式运用】‎ ‎1.(2016×大庆)如图，在Rt△ABC中，∠C＝90°，以BC为直径的⊙O交斜边AB于点M，若H是AC的中点，连接MH. ‎ ‎(1)求证：MH为⊙O的切线. ‎ ‎(2)若MH＝，tan∠ABC＝，求⊙O的半径.‎ ‎(3) 在（2）的条件下分别过点A、B作⊙O的切线，两切线交于点D，AD与⊙O相切于N点，过N点作NQ⊥BC，垂足为E，且交⊙O于Q点，求线段NQ的长度. ‎ 解：（1）连接OH、OM，‎ ‎∵H是AC的中点，O是BC的中点，‎ ‎∴OH是△ABC的中位线，∴OH∥AB，‎ ‎∴∠COH＝∠ABC，∠MOH＝∠OMB，‎ 图5-2‎ 又∵OB＝OM，∴∠OMB＝∠MBO，‎ ‎∴∠COH＝∠MOH，‎ 在△COH与△MOH中，‎ ‎，∴△COH≌△MOH（SAS），‎ ‎∴∠HCO＝∠HMO＝90°，‎ ‎∴MH是⊙O的切线；‎ 图b ‎（2）∵MH、AC是⊙O的切线，‎ ‎∴HC＝MH＝，∴AC＝2HC＝3，‎ ‎∵tan∠ABC＝，∴＝，‎ ‎∴BC＝4，∴⊙O的半径为2. ‎ ‎（3）连接OA、CN、ON，OA与CN相交于点I，‎ ‎∵AC与AN都是⊙O的切线，‎ ‎∴AC＝AN，AO平分∠CAD，‎ ‎∴AO⊥CN，‎ ‎∵AC＝3，OC＝2，‎ 图c ‎∴由勾股定理可求得：‎ AO＝，‎ ‎∵AC•OC＝AO•CI，∴CI＝，∴由垂径定理可求得：CN＝，‎ 设OE＝x，由勾股定理可得：CN2﹣CE2＝ON2﹣OE2，‎ ‎∴﹣（2＋x）2＝4﹣x2，‎ ‎∴x＝，∴CE＝，由勾股定理可求得：EN＝，‎ ‎∴由垂径定理可知：NQ＝2EN＝．‎ ‎2.(2016×广西梧州)如图，AB、BC、CD分别与⊙O切于E、F、G，且AB∥CD．连接OB、OC，延长CO交⊙O于点M，过点M作MN∥OB交CD于N．‎ ‎（1）求证：MN是⊙O的切线；‎ ‎（2）当OB＝6cm，OC＝8cm时，求⊙O的半径及MN的长．‎ ‎(1)如图所示，连接OE、OF、OG.‎ ‎∵OE、OF、OG都是⊙O的半径，‎ ‎∴OE＝OG＝OG.‎ ‎∵AB、BC、CD分别与⊙O相切于点E、F、G，‎ 图5-2‎ ‎∴∠OEB＝∠OFB＝∠OFC＝∠OGC＝90.‎ 在Rt△OEB和Rt△OFB中，‎ ‎，‎ ‎∴Rt△OEB≌Rt△OFB，‎ 则∠OBE＝∠OBF.‎ 同理可证Rt△OFC≌Rt△OGC，‎ 则∠OCF＝∠OCG.‎ 图d ‎∵AB∥CD,‎ ‎∴∠OBE＋∠OBF＋∠OCF＋∠OCG＝180，‎ 即∠OBF＋∠OCF＝90°，‎ 则∠BOC＝180°－∠OBF－∠OCF＝90°. ∵MN∥OB，‎ ‎∴∠NMC＝∠MOB＝180°－∠BOC＝90°，‎ 即OM⊥MN,又∵OM是⊙O的半径，‎ ‎∴MN是⊙O的切线。‎ ‎(2)如图所示，由（1）可得，‎ 在Rt△OBC中，OF⊥BC，∠BOC＝90°。‎ 由勾股定理得，，‎ 则，‎ 即10OF＝48,故OF＝4.8.∵OM＝OF＝4.8，‎ ‎∴MC＝OM＋OC＝12.8。‎ 由（1）知，∠OCB＝∠MCN，∠NMC∠BOC＝90°，‎ 则△NMC∽△BOC，因此，即，‎ 故。‎ 综上所述，⊙O的半径为4.8cm，MN的长为9.6cm.‎ ‎3.（2018·湖北襄阳）如图，AB是⊙O的直径，AM和BN是⊙O的两条切线， E为⊙O上一点，过点E作直线DC分别交AM，BN于点D，C，且CB＝CE．‎ ‎(1)求证：DA＝DE；‎ ‎(2)若AB＝6，CD＝4，求图中阴影部分的面积．‎ 解：（1）证明：连结OE，OC.‎ 图5-3‎ ‎∵BN切⊙O于点B，∴∠OBN＝90°.‎ ‎∵OE＝OB，OC＝OC，CE＝CB，∴△OEC≌△OBC.‎ ‎∴∠OEC＝∠OBC＝90°.‎ ‎∴CD是⊙O的切线.‎ ‎∵AD切⊙O于点A，∴DA＝DE.‎ ‎（2）过点D作DF⊥BC于点F，则四边形ABFD是矩形.‎ ‎∴AD＝BF，DF＝AB＝6.‎ ‎∴DC＝BC＋AD＝4.‎ ‎∵FC＝.‎ 图e ‎∴BC－AD＝2. BC－AD＝2.∴BC＝3.‎ 在Rt△OBC中，tan∠BOC＝，‎ ‎∴∠BOC＝60°. ∵△OEC≌△OBC，∴∠BOE＝2∠BOC＝120°.‎ ‎∴S阴影部分＝S四边形BCEO－S扇形OBE＝2××BC×OB－×p×OB2＝9－3p.‎