2018中考几何题
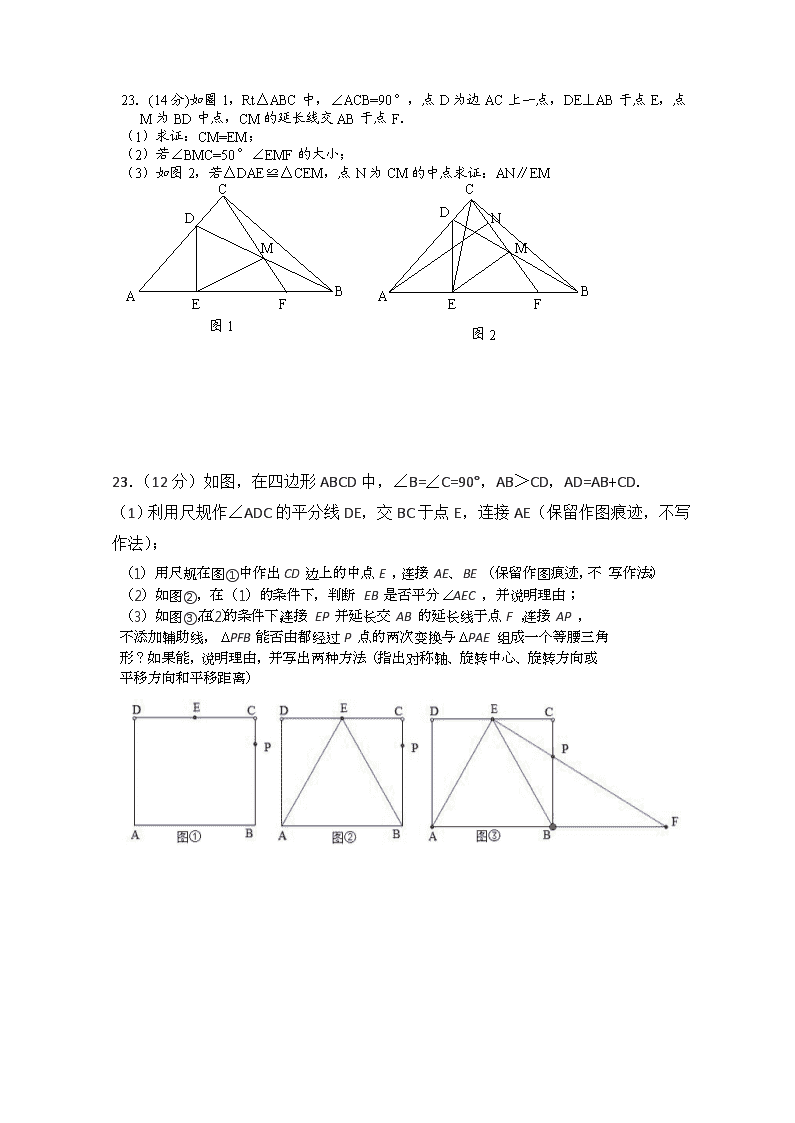
23.(14分)如圈1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,CM的延长线交AB于点F.
(1)求证:CM=EM;
(2)若∠BMC=50°∠EMF的大小;
A
B
C
D
M
E
F
N
图2
A
B
C
D
E
F
M
图1
(3)如图2,若△DAE≌△CEM,点N为CM的中点求证:AN∥EM
23.(12分)如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.
(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);
(1)用尺规在图①中作出 CD 边上的中点 E ,连接 AE、BE (保留作图痕迹,不 写作法);
(2)如图②,在(1)的条件下,判断 EB 是否平分 ÐAEC ,并说明理由;
(3)如图③,在(2)的条件下,连接 EP 并延长交 AB 的延长线于点 F ,连接 AP ,
不添加辅助线, DPFB 能否由都经过 P 点的两次变换与 DPAE 组成一个等腰三角
形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向或
平移方向和平移距离)
图11
C
B
A
D
23.(12分)如图11,在四边形ABCD中,∠B=∠C=,AB>CD,AD=AB+CD.
(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);
(2)在(1)的条件下
①证明:AE⊥DE;
②若CD=2,AB=4,点M,N分别是AE,AB上的动点,
求BM+ACN的最小值
25.(14分)如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.
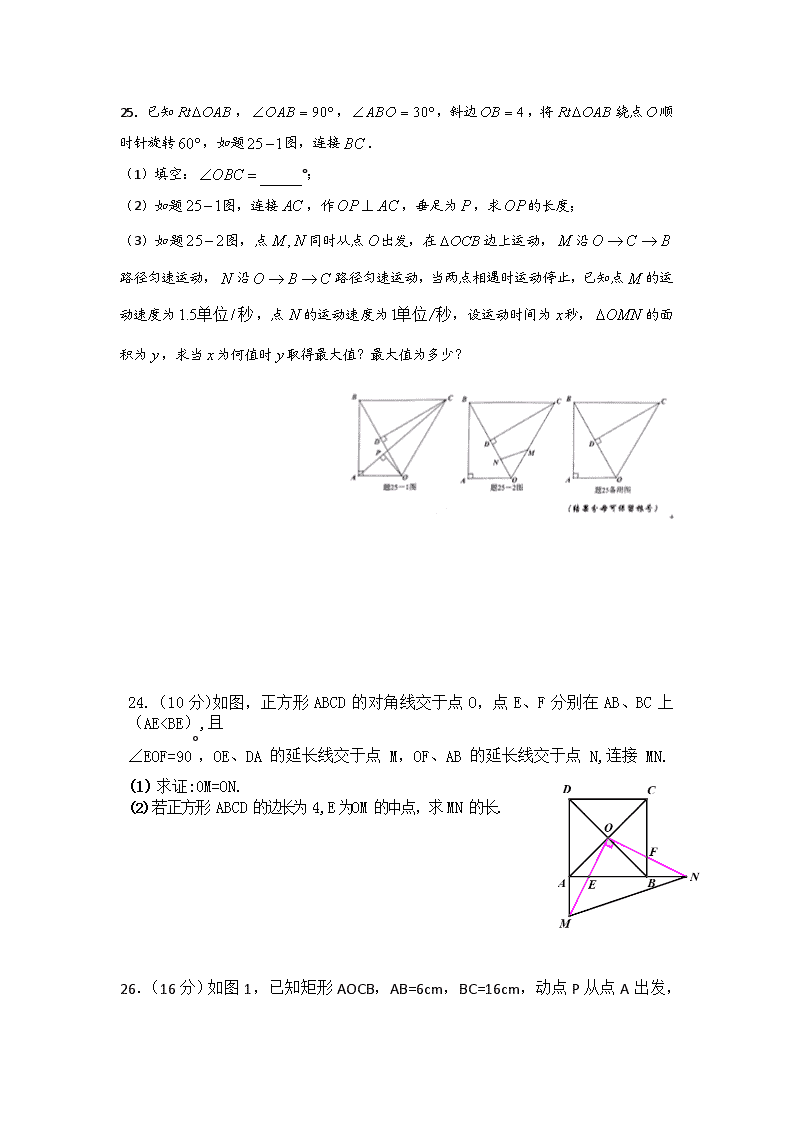
25.已知,,,斜边,将绕点顺时针旋转,如题图,连接.
(1)填空: °;
(2)如题图,连接,作,垂足为,求的长度;
(3)如题图,点同时从点出发,在边上运动,沿路径匀速运动,沿路径匀速运动,当两点相遇时运动停止,已知点的运动速度为,点的运动速度为,设运动时间为秒,的面积为,求当为何值时取得最大值?最大值为多少?
24.(10 分)如图,正方形 ABCD 的对角线交于点 O,点 E、F 分别在 AB、BC 上(AE
0),GA=y米,已知y与x之间的函数关系如图所示.
(1)求图②中线段MN所在直线的函数表达式;
(2)试问小明从起点A出发直至最后回到点A处,所走过的路径(即△EFG)是否可以是一个等腰三角形?如果可以.求出相应x的值;如果不可以,说明埋由.
24.如图,在平行四边形ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA.BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG, 连接EH.
(1)若,AB=13,求AF的长;
(2)求证:EB=EH.
28.如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=∠DEF=90°,∠EDF=30°
【操作】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上,再将三角板DEF绕点E旋转,并使边DE与边AB交于点P,边EF与边BC于点Q
【探究一】在旋转过程中,
(1) 如图2,当时,EP与EQ满足怎样的数量关系?并给出证明.
(1) 如图3,当时EP与EQ满足怎样的数量关系?,并说明理由.
(2) 根据你对(1)、(2)的探究结果,试写出当时,EP与EQ满足的数量关系式
为_________,其中的取值范围是_______(直接写出结论,不必证明)
【探究二】若,AC=30cm,连续PQ,设△EPQ的面积为S(cm2),在旋转过程中:
(1) S是否存在最大值或最小值?若存在,求出最大值或最小值,若不存在,说明理由.
(2) 随着S取不同的值,对应△EPQ的个数有哪些变化?不出相应S值的取值范围.
(图3)
(图3)
(图2)
(图1)
如图1,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
问题解决
(1)直接写出图1中tan∠CPN的值为 ;
(2)如图2,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值;
思维拓展
(3)如图3,AB⊥BC,AB=4BC,点M在AB上,且AM=BC,延长CB到N,使BN=2BC,连接AN交CM的延长线于点P,用上述方法构造网格求∠CPN的度数.
25.阅读下面材料:
小明遇到这样一个问题:
如图1,△ABC中,∠ACB=90°,点D在AB上,且∠BAC=2∠DCB,求证:AC=AD.
小明发现:除了直接用角度的方法外,还可以用下面两种方法:
方法1:如图2,作AE平分∠CAB,与CD相交于点E.
B
A
D
C
(图1)
(图3)
B
A
D
C
F
E
B
A
D
C
(图2)
方法2:如图3,作∠CDF=∠DCB,与AB相交于点F.
(1)根据阅读材料,任选一种方法,证明:AC=AD;
用学过的知识或参考小明的方法,解决下面的问题:
(2)如图4,△ABC中,点D在AB上,点E在BC上,且∠BDE=2∠ABC,点F在BD上,且∠AFE=∠BAC,延长DC、FE,相交于点G,且∠DGF=∠BDE.
①在图中找出与DEF相等的角,并加以证明;
②若AB=kDF,猜想线段DE与DB数量关系,并证明你的猜想.
B
A
D
C
E
F
G
(图4)
23.如图,在平面直角坐标系中,点F的坐标为(0,10),点E的坐标为(20,0),直线l1经过点F和点E,直线11与直线12:y=x相交于点P
(1)求直线的表达式和点P的坐标;
(2)矩形ABCD的边AB在y轴轴的正半轴上,点A与点F重合,点B在线段OF上,边AD平行于X轴,且AB=6,AD=9,将矩形ABCD沿射线FE的方向平移,边AD始终与x轴平行,已知矩形ABCD以每秒个单位的速度匀速移动动(点A移动到点E时停止移动),设移动时间为t秒(t>0),
①矩形ABCD在移动过程中,B、C、D三点中有且只有一个顶点落在直线11或12上,请直接写出此时t的值;
②若矩形ABCD在移动的过程中,直线CD交直线11于点N,交直线于点M,当△PMN的面积等于18时,请直接写出此时t的值.
25.(13分)已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.
24.已知△ABC是等腰三角形,CA=CB,0°<∠ACB≤90°,点M在边AC上,点N在边BC上(点M、点N不与所在线段端点重合),BN=AM,连接AN,BM.射线AG∥BC,延长BM交射线AG于点D,点E在直线AN上,且AE=DE.
(1)如图,当∠ACB=90°时,
①求证:△BCM≌△CAN;
②求∠BDE的度数;
(2)当∠ACB=,其它条件不变时,∠BDE的度数是(用含的代数式表示)
(3)若△ABC是等边三角形,AB=,点N是BC边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长
26.如图:一次函数 的图象与坐标轴交于A、B两点,点P是函数
(0<x<4)图象上任意一点,过点P作PM⊥y轴于点M,连接OP.
(1)当AP为何值时,△OPM的面积最大?并求出最大值;
(2)当△BOP为等腰三角形时,试确定点P的坐标.
24.(12分)再读教材:
宽与长的比是(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,下面,我们用宽为2的矩形纸片折叠黄金矩形.(提示:MN=2)
第一步,在矩形纸片一端,利用图①
的方法折出一个正方形,然后把纸片展平.
第二步,如图②,把这个正方形折成两个相等的矩形,再把纸片展平.
第三步,折出内侧矩形的对角线AB,并把AB折到图①中所示的AD处.
第四步,展平纸片,按照所得的点D折出DE,使DE⊥ND,则图④中就会出现黄金矩形.
问题解决:
(1)图③中AB= (保留根号);
(2)如图③,判断四边形BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
实际操作
(4)结合图④,请在矩形BCDE中添加一条线段,设计一个新的黄金是形,用字母表示出来,并写出它的长和宽.
23.(10分)问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将:矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD.并且量得AB=2cm,AC=4cm.
操作发现:
(1)将图1中的△ACD以点A为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到如图2所示的△AC′D,过点C作AC′的平行线,与DC'的延长线交于点E,则四边形ACEC′的形状是 .
(2)创新小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B、A、D三点在同一条直线上,得到如图3所示的△AC′D,连接CC',取CC′的中点F,连接AF并延长至点G,使FG=AF,连接CG、C′G,得到四边形ACGC′,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至A'点,A'C与BC′相交于点H,如图4所示,连接CC′,试求tan∠C′CH的值.
24.(本题满分10分)
(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,
AO=,∠ABC=∠ACB=75°, BO:OD=1:3,求DC的长.
(第24题图3)
(第24题图2)
(第24题图1)
23.(11分)如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,CD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.
(3)若∠B=30°,判定四边形AEGF是否为菱形,并说明理由.
24.(12分)已知:如图,四边形ABCD,AB∥DC,CB⊥AB,AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s.点P和点Q同时出发,以QA、QP为边作平行四边形AQPE,设运动的时间为t(s),0<t<
5.根据题意解答下列问题:
(1)用含t的代数式表示AP;
(2)设四边形CPQB的面积为S(cm2),求S与t的函数关系式;
(3)当QP⊥BD时,求t的值;
(4)在运动过程中,是否存在某一时刻t,使点E在∠ABD的平分线上?若存在,求出t的值;若不存在,请说明理由.
25.(12分)如图,在菱形ABCD中,AC与BD交于点O,E是BD上一点,EF∥AB,∠EAB=∠EBA,过点B作DA的垂线,交DA的延长线于点G.
(1)∠DEF和∠AEF是否相等?若相等,请证明;若不相等,请说明理由;
(2)找出图中与△AGB相似的三角形,并证明;
(3)BF的延长线交CD的延长线于点H,交AC于点M.求证:BM2=MF•MH.
24.(12分)如图1,在▱ABCD中,DH⊥AB于点H,CD的垂直平分线交CD于点E,交AB于点F,AB=6,DH=4,BF:FA=1:5.
(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.
①求四边形BHMM′的面积;
②直线EF上有一动点N,求△DNM周长的最小值.
(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.
24.(10分)如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2,求BE的长.
23.(9分)(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△
ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是 ;位置关系是 .
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.
22.综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形中,,是延长线上一点,且,连接,交于点,以为一边在的左下方作正方形,连接.试判断线段与的位置关系.
探究展示:勤奋小组发现,垂直平分,并展示了如下的证明方法:
证明:∵,∴.
∵,∴.
∵四边形是矩形,∴.
∴.(依据1)
∵,∴.∴.
即是的边上的中线,
又∵,∴.(依据2)
∴垂直平分.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点是否在线段的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接,以为一边在的左下方作正方形,发现点在线段的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接,以为一边在的右上方作正方形,可以发现点,点都在线段的垂直平分线上,除此之外,请观察矩形和正方形的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.
25.(本题满分14分,第(1)小题满分4分,笫(2)小题满分5分,第(3) 小题满分小题5分)
已知⊙O的直径AB=2,弦AC与弦BD交于点E,且OD⊥AC,垂足为点F.
(1)如图11,如果AC=BD,求弦AC的长;
(2)如图12,如果E为弦BD的中点,求∠ABD的余切值;
(3)连接BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的
内接正(n+4)边形的一边,求△ACD的面积.
A
B
O
备用图
O
B
A
C
D
E
F
图12
A
B
C
D
F
E
O
图11
如图,在□ABCD中,点E是CD的中点,点F是BC边上的点,AF=AD+FC.
□ABCD的面积为S,由A、E、F三点确定的圆的周长为l.
(1)若△ABE的面积为30,直按写出S的值;
B
A
D
C
E
F
(2)求证:AE平分∠DAF;
(3)若AE=BE,AB=4,AD=5,求l的值.
25.(本题满分12分)问题提出 (1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为.
问题探究 (2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决 (3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在BC线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
图①图②图③
27.(10分)在Rt△ABC中,∠ABC=90°,AB=,AC=2,过点B作直线m∥AC,将△ABC绕点C顺时针旋转得到△A′B′C′(点A,B的对应点分别为A',B′),射线CA′,CB′分別交直线m于点P,Q.
(1)如图1,当P与A′重合时,求∠ACA′的度数;
(2)如图2,设A′B′与BC的交点为M,当M为A′B′的中点时,求线段PQ的长;
(3)在旋转过程中,当点P,Q分别在CA′,CB′的延长线上时,试探究四边形PA'B′Q的面积是否存在最小值.若存在,求出四边形PA′B′Q的最小面积;若不存在,请说明理由.
22.(8分)如图,在平面直角坐标系中,点O1的坐标为(﹣4,0),以点O1为圆心,8为半径的圆与x轴交于A,B两点,过A作直线l与x轴负方向相交成60°的角,且交y轴于C点,以点O2(13,5)为圆心的圆与x轴相切于点D.
(1)求直线l的解析式;
(2)将⊙O2以每秒1个单位的速度沿x轴向左平移,当⊙O2第一次与⊙O1外切时,求⊙O2平移的时间.
24.(12分)如图,已知△ABC的顶点坐标分别为A(3,0),B(0,4),C(﹣3,0).动点M,N同时从A点出发,M沿A→C,N沿折线A→B→C,均以每秒1个单位长度的速度移动,当一个动点到达终点C时,另一个动点也随之停止移动,移动的时间记为t秒.连接MN.
(1)求直线BC的解析式;
(2)移动过程中,将△AMN沿直线MN翻折,点A恰好落在BC边上点D处,求此时t值及点D的坐标;
(3)当点M,N移动时,记△ABC在直线MN右侧部分的面积为S,求S关于时间t的函数关系式.
24. 在平面直角坐标系中,四边形是矩形,点,点,点.以点为中心,顺时针旋转矩形,得到矩形,点,,的对应点分别为,,.
(Ⅰ)如图①,当点落在边上时,求点的坐标;
(Ⅱ)如图②,当点落在线段上时,与交于点.
①求证;
②求点的坐标.
(Ⅲ)记为矩形对角线的交点,为的面积,求的取值范围(直接写出结果即可).
23.(本小题12分)如图1.在矩形ABCD中,P为CD边上一点(DP<CP)∠APB=90°.将△ADP沿AP翻折得到△AD'P,PD' 的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
(1)求证:AD2=DP·PC
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别别交PM,PB于点E,F.若=,求的值.
F
A
B
C
D
P
M
N
D'
E
(图2)
(图1)
A
B
C
D
P
M
N
D'
23.如图,在正方形ABCD中,点G在边BC上(不与点B、C重合),连接AG,作DE⊥AG,于点E,BF⊥AG于点F,设
(1)求证:AE=BF
(2)连接BE、DF,设,求证:
(3)设线段AG与对角线BD交于点H, 和四边形CDHG的面积分别为
,求的最大值.
24.(12分)我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.
(1)概念理解:如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求的值.
(3)应用拓展:如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
22.(10分)如图,抛物线y=ax2+bx(a≠0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.
(1)求抛物线的函数表达式.
(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?
(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.
23.(10分)如图,四边形ABCD的四个顶点分别在反比例函数y=与y=(x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.
24.(12分)在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.
(1)如图,点D在线段CB上,四边形ACDE是正方形.
①若点G为DE中点,求FG的长.
②若DG=GF,求BC的长.
(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
25.(12分)若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足条件的AC的长;
(2)如图1,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC.求证:△ABC是比例三角形.
(3)如图2,在(2)的条件下,当∠ADC=90°时,求的值.
26.(14分)如图1,直线l:y=﹣x+b与x轴交于点A(4,0),与y轴交于点B,点C是线段OA上一动点(0<AC<).以点A为圆心,AC长为半径作⊙A交x轴于另一点D,交线段AB于点E,连结OE并延长交⊙A于点F.
(1)求直线l的函数表达式和tan∠BAO的值;
(2)如图2,连结CE,当CE=EF时,
①求证:△OCE∽△OEA;
②求点E的坐标;
(3)当点C在线段OA上运动时,求OE•EF的最大值.
24.(12分)如图,Rt△OAB的直角边OA在x轴上,顶点B的坐标为(6,8),直线CD交AB于点D(6,3),交x轴于点C(12,0).
(1)求直线CD的函数表达式;
(2)动点P在x轴上从点(﹣10,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t.
①点P在运动过程中,是否存在某个位置,使得∠PDA=∠B?若存在,请求出点P的坐标;若不存在,请说明理由;
②请探索当t为何值时,在直线l上存在点M,在直线CD上存在点Q,使得以OB为一边,O,B,M,Q为顶点的四边形为菱形,并求出此时t的值.
24.(10分)如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.
(1)若AH=3,HE=1,求△ABE的面积;
(2)若∠ACB=45°,求证:DF=CG.