2016中考数学二轮专题复习试卷四边形

2016中考数学二轮专题复习试卷四边形

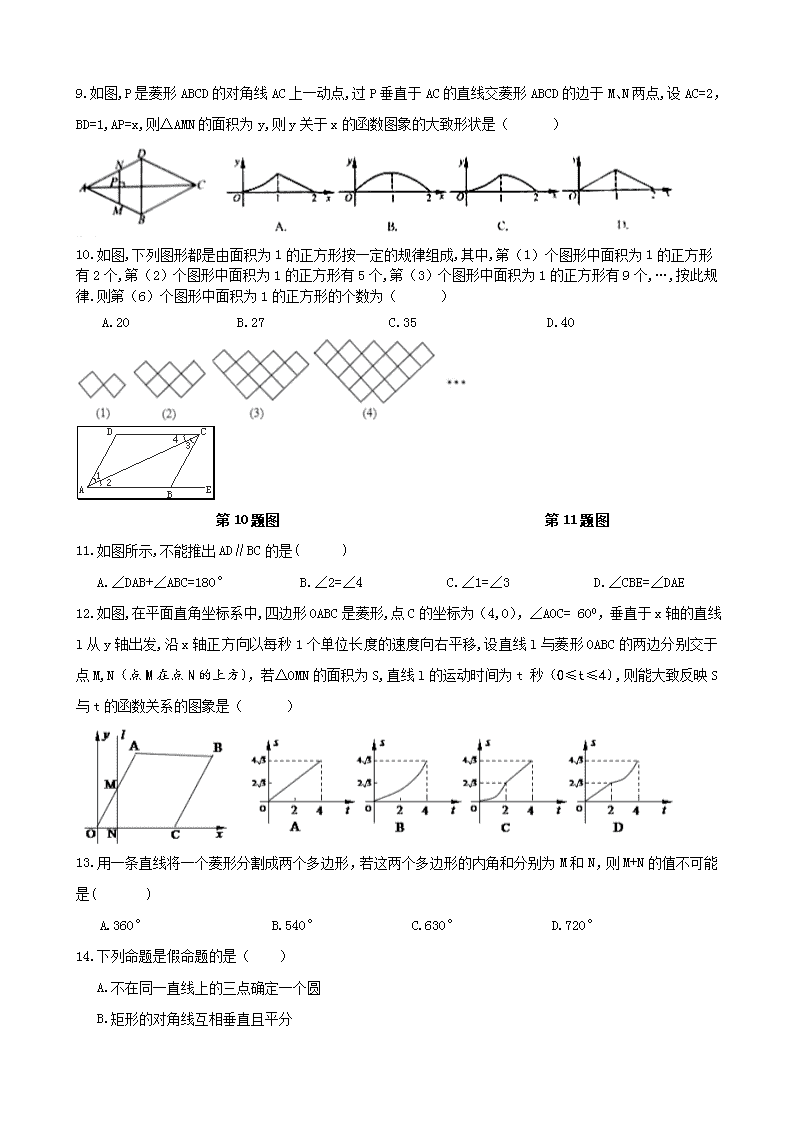
第03课 四边形专题复习 ‎1.以三角形的三个顶点及三边中点为顶点的平行四边形共有（ ） ‎ ‎ A.1个 B.2个 C.3个 D.4个 ‎2.某商店出售下列四种形状的地砖：①正三角形;②正方形;③正五边形;④正六边形.若只选购其中一种地砖镶嵌地面，可供选择的地砖共有（ ）‎ ‎ A.4种 B.3种 C.2种 D.1种 ‎3.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是（ ）‎ ‎ A.AB=CD B.AD=BC C.AB=BC D.AC=BD ‎ ‎ ‎ 第3题图 第4题图 第5题图 ‎ ‎4.如图,正方形ABCD中,对角线AC、BD交于O,点M、N分别为OB、OC中点,则cos∠OMN值为( )‎ A. B. C. D.1 ‎ ‎5.如图,在菱形ABCD中,DE⊥AB,,BE=2,则tan∠DBE的值是( )‎ ‎ A. B.2 C. D.‎ ‎6.如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,,则下列结论正确的个数有( )‎ ‎ ①DE=3cm；②BE=1cm；③菱形的面积为15cm2；④‎ ‎ A.1个 B.2个 C.3个 D.4个 ‎ ‎ ‎ 第6题图 第7题图 第8题图 ‎ ‎7.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=900，BC=5,点A、B的坐标分别为（1,0）、（4,0），将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为（ ）‎ A.4 B.8 C.16 D.‎ ‎8.在平行四边形ABCD中，点A1、A2、A3、A4和C1、C2、C3、C4分别AB和CD的五等分点,点B1、B2和D1、D2分别是BC和DA的三等分点,已知四边形A4 B2 C4 D2的积为1,则平行四边形ABCD面积为（ ）‎ ‎ A.2 B. C. D.15‎ ‎9.如图,P是菱形ABCD的对角线AC上一动点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2，BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是（ ）‎ ‎10.如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第（1）个图形中面积为1的正方形有2个,第（2）个图形中面积为1的正方形有5个,第（3）个图形中面积为1的正方形有9个,…,按此规律.则第（6）个图形中面积为1的正方形的个数为（　 　）‎ ‎　 A.20 B.27 C.35 D.40‎ ‎ ‎ ‎ 第10题图 第11题图 ‎ ‎11.如图所示,不能推出AD∥BC的是( )‎ ‎ A.∠DAB+∠ABC=180° B.∠2=∠4 C.∠1=∠3 D.∠CBE=∠DAE ‎12.如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为（4,0），∠AOC= 600，垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N（点M在点N的上方），若△OMN的面积为S,直线l的运动时间为t 秒（0≤t≤4）,则能大致反映S与t的函数关系的图象是（ ）‎ ‎13.用一条直线将一个菱形分割成两个多边形，若这两个多边形的内角和分别为M和N，则M+N的值不可能是( )‎ ‎ A.360° B.540° C.630° D.720°‎ ‎14.下列命题是假命题的是（　　）‎ ‎ A.不在同一直线上的三点确定一个圆 ‎ B.矩形的对角线互相垂直且平分 ‎ C.正六边形的内角和是720°‎ ‎ D.角平分线上的点到角两边的距离相等 ‎15.如图,矩形ABCD中,AB＞AD，AB=a，AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N．则DM+CN的值为（用含a的代数式表示）( )‎ ‎ A.a B. 　 C. D.‎ ‎ ‎ ‎ 第15题图 第16题图 第17题图 ‎16.如图,点F是□ABCD的边CD上一点,直线BF交AD的延长线与点E,则下列结论错误的是（　 　）‎ ‎ A. B. C. D. ‎17.如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为（　　）‎ ‎ A. B. C. D.6‎ ‎18.如图,一个四边形花坛ABCD,被两条线段MN,EF分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S1,S2,S3,S4，若MN∥AB∥DC，EF∥DA∥CB,则有（ ）‎ ‎ A.S1=S4 B.S1+S4=S2+S3 C.S1S4=S2S3 D.都不对 ‎ ‎ ‎ 第18题图 第19题图 ‎19.如图,正方形ABCD边长为2,G在CD的延长线上,四边形CEFG也为正方形,则△DBF面积为（ ）‎ A.4 B. C. D. 2‎ ‎20.如图,在平行四边形ABCD中,DB=DC,∠A=650，CEBD于E,则∠BCE= ． ‎ ‎ ‎ ‎ 第20题图 第21题图 第22题图 ‎ ‎21.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C/处,折痕为EF，若∠ABE=200，那么∠EFC/的度数为 度．‎ ‎22.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP =EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤．其中正确结论的序号是 ‎ ‎23.如图,在平行四边形ABCD中,CD=10,F是AB边上一点,DF交AC于点E,‎ 且= ，BF= .‎ ‎ ‎ ‎ 第23题图 第24题图 第25题图 ‎ ‎24.如图,已知菱形ABCD，其顶点A、B在数轴上对应的数分别为－4和1，则BC=_____.‎ ‎25.在如图所示3×3的正方形方格图案中有_______个正方形.‎ ‎26.如图,菱形ABCD的对角线AC、BD相交于点O，且AC=8，BD=6，过点O作OH⊥AB，垂足为H，则点O到边AB的距离OH＝ ．‎ ‎ ‎ ‎ 第26题图 第27题图 第28题图 ‎ ‎27.如图，矩形纸片ABCD中,AB=2cm,点E在BC上，且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点重合,则AC＝ cm.‎ ‎28.如图,菱形ABCD的边长为2cm,∠A=600．弧BD是以点A为圆心、AB长为半径的弧,弧CD是以点B为圆心、BC长为半径的弧.则阴影部分的面积为 cm2．‎ ‎29.如图,在平面直角坐标系中,点O为原点,菱形OABC的对角线OB在x轴上,顶点A在反比例函数的图像上,则菱形的面积为___________‎ ‎ ‎ ‎ 第29题图 第30题图 第31题图 第32题图 ‎ ‎30.如图，正方形ABCD的面积为25，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为_____________。‎ ‎31.如图，点O是△ABC所在平面内一动点，连接OB、OC,并把AB、OB、OC、CA的中点D、E、F、G顺次连接起来，若四边形DEFG为正方形，则点O所在的位置满足的条件是_______________________.‎ ‎32.如图,在平面直角坐标系中,已知点A（1,1），B（﹣1,1），C（﹣1,﹣2），D（1,﹣2），把一根长为2014个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在A处，并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是　 　．‎ ‎33.如图,用两张等宽的纸带交叉重叠地放在一起,重合的四边形是菱形吗？如果是菱形请给出证明，如果不是菱形请说明理由．‎ A B C D ‎34.如图,矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE于F,连结DE.求证：DF=DC．‎ ‎35.已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.‎ ‎36.如图（1），在△ABC和△EDC中,AC=CE=CB=CD,∠ACB=∠ECD=900，AB与CE交于F，ED与AB、BC分别交于M、H．‎ ‎(1)求证:CF=CH；‎ ‎(2)如图(2),△ABC不动,将△EDC绕点C旋转到∠BCE=450时，试判断四边形ACDM是什么四边形？并证明你的结论．‎ ‎37.如图,菱形ABCD中,∠B=60º,点E在边BC上,点F在边CD上．‎ ‎(1)如图1,若E是BC的中点,∠AEF=60º,求证：BE=DF；‎ ‎(2)如图2,若∠EAF=60º,求证：△AEF是等边三角形．‎ ‎38.如图,在菱形ABCD中,∠A=600，点P、Q分别在边AB、BC上,且AP=BQ．‎ ‎（1）求证：△BDQ≌△ADP；（2）已知AD=3,AP=2,求cos∠BPQ的值（结果保留根号）．‎ ‎39.如图，菱形ABCD的边长为2，BD=2，E、F分别是边AD，CD上的两个动点，且满足AE+CF=2.‎ ‎（1）求证：△BDE≌△BCF； ‎ ‎（2）判断△BEF的形状，并说明理由；‎ ‎（3）设△BEF的面积为S，求S的取值范围.‎ ‎40.问题背景：‎ ‎（1）如图，△ABC中，DE∥BC分别交AB，AC于D，E两点，过点E作EF∥AB交BC于点F．请按图示数据填空：四边形DBFE的面积 ，△EFC的面积 ，△ADE的面积 ．‎ 探究发现：（2）在（1）中，若，，DE与BC间的距离为．请证明．‎ ‎41.正方形ABCD边长为4,M,N分别是BC、CD上两个动点,当M点在BC上运动时,保持AM和MN垂直.‎ ‎（1）证明：Rt△ABM∽Rt△MCN；‎ ‎（2）设BM=x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN面积最大，并求出最大面积；‎ ‎（3）当M点运动到什么位置时Rt△ABM∽Rt△AMN，求此时的值．‎ ‎42.如图,在矩形ABCD中,AB=12cm,BC=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s，当点F追上点G（即点F与点G重合）时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S（cm2）．‎ ‎（1）当t=1秒时,S的值是多少？‎ ‎（2）写出S和t之间的函数解析式,并指出自变量t的取值范围．‎ ‎（3）若点F在矩形的边BC上移动,当t为何值时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似？请说明理由．‎ ‎43.如图,P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在射线BC上，且PE=PB.‎ ‎（1）求证：① PE=PD;② PE⊥PD；‎ ‎（2）设AP=x, △PBE的面积为y.‎ ‎ ① 求出y关于x的函数关系式，并写出x的取值范围；‎ ‎ ② 当x取何值时，y取得最大值，并求出这个最大值.‎ ‎ ‎ ‎44.已知：正方形ABCD中，∠MAN=450，∠MAN绕点A顺时针旋转，它的两边分别交CB,DC（或它们的延长线）于点M,N．‎ 当∠MAN绕点A旋转到BM=DN时（如图1），易证BM+DN=MN．‎ ‎（1）当∠MAN绕点A旋转到时（如图2），线段BM,DN和MN之间有怎样的数量关系？写出猜想，并加以证明．‎ ‎（2）当∠MAN绕点A旋转到如图3的位置时，线段BM,DN和MN之间又有怎样的数量关系？请直接写出你的猜想．‎ B B M B C N C N M C N M 图1‎ 图2‎ 图3‎ A A A D D D