2009年湖南省张家界市初中毕业学业考试试卷及答案

2009年湖南省张家界市初中毕业学业考试试卷及答案

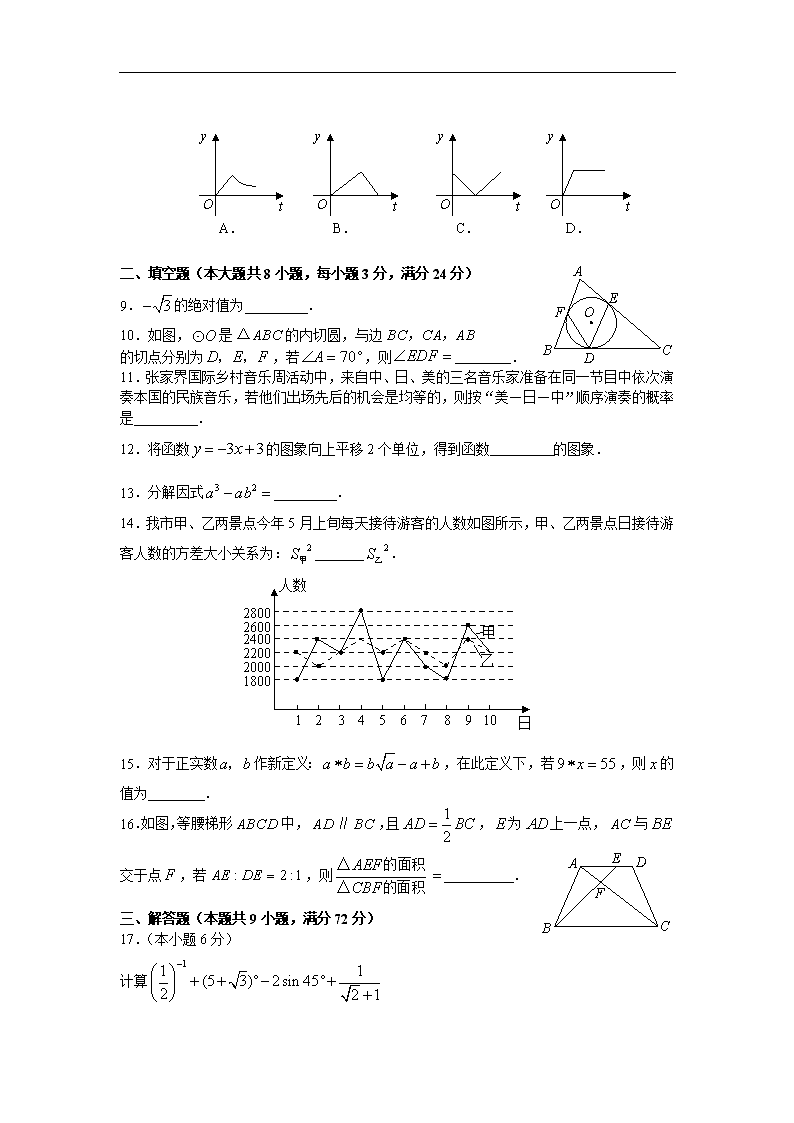
张家界市2009年初中毕业学业考试试卷 数 学 考生注意：本学科试卷共三道大题25小题，满分120分，考试时量120分钟．‎ 一、选择题（本大题共8小题，每小题3分，满分24分）‎ ‎1．在实数0，，，0.74，中，无理数有（ ）‎ A．1个 B．2个 C．3个 D．4个 ‎2．用计算器求值时，需相继按“‎2”‎，“”，“‎3”‎，“”键，若小红相继按“”，“‎2”‎，“”，“‎4”‎，“”键，则输出结果是（ ）‎ A．4 B．‎5 ‎ C．6 D．16‎ ‎3．下图所示的几何体的主视图是（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎4．不等式组的解集在数轴上表示为（ ）‎ ‎0‎ ‎6‎ A．‎ ‎0‎ ‎6‎ B．‎ ‎0‎ ‎6‎ C．‎ ‎0‎ ‎6‎ D．‎ ‎5．下列运算正确的是（ ）‎ A． B．‎ C． D．‎ ‎6．下列不是必然事件的是（ ）‎ A．两直线相交，对顶角相等 ‎ B．三角形的外心到三个顶点的距离相等 E D C A B ‎1‎ C．三角形任意两边之和大于第三边 D．两相似多边形面积的比等于周长的比 ‎7．如图，，且，，‎ 则的度数是（ ）‎ A． B． ‎ C． D．‎ ‎8．为了预防“HINI”流感，某校对教室进行药熏消毒，药品燃烧时，室内每立方米的含药量与时间成正比；燃烧后，室内每立方米含药量与时间成反比，则消毒过程中室内每立方米含药量与时间的函数关系图象大致为（ ）‎ y t O A．‎ y t O B．‎ y t O C．‎ y t O D．‎ A E C D O B F 二、填空题（本大题共8小题，每小题3分，满分24分）‎ ‎9．的绝对值为 ．‎ ‎10．如图，是的内切圆，与边 的切点分别为，若，则 ．‎ ‎11．张家界国际乡村音乐周活动中，来自中、日、美的三名音乐家准备在同一节目中依次演奏本国的民族音乐，若他们出场先后的机会是均等的，则按“美—日—中”顺序演奏的概率是 ．‎ ‎12．将函数的图象向上平移2个单位，得到函数 的图象．‎ ‎13．分解因式 ．‎ ‎14．我市甲、乙两景点今年5月上旬每天接待游客的人数如图所示，甲、乙两景点日接待游客人数的方差大小关系为： ．‎ 人数 ‎2800‎ ‎2600‎ ‎2400‎ ‎2200‎ ‎2000‎ ‎1800‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 日 甲 乙 ‎15．对于正实数作新定义：，在此定义下，若，则的值为 ．‎ A E D C F B ‎16．如图，等腰梯形中，，且，为上一点，与交于点，若，则 ．‎ 三、解答题（本题共9小题，满分72分）‎ ‎17．（本小题6分）‎ 计算 ‎18．（本小题6分）‎ D B A C 小明将一幅三角板如图所示摆放在一起，发现只要知道其中一边的长就可以求出其它各边的长，若已知，求的长．‎ ‎19．先化简，后求值（本小题6分）‎ 其中 ‎20．（本小题6分）‎ 在建立平面直角坐标系的方格纸中，每个小方格都是边长为1的小正方形，的顶点均在格点上，点的坐标为，请按要求画图与作答 （1） 把绕点旋转得．‎ ‎（2）把向右平移7个单位得．‎ ‎（3）与是否成中心对称，若是，找出对称中心，并写出其坐标．‎ A C B P OP xP yP ‎21．列方程解应用题（本小题9分）‎ ‎“阳黄公路”开通后，从长沙到武陵源增加了一条新线路，新线路里程在原线路长‎360Km的基础上缩短了‎50Km，今有一旅游客车和小车同时从长沙出发前往武陵源，旅游客车走新线路，小车因故走原线路，中途停留6分钟．若小车速度是旅游客车速度的1.2倍，且两车同时到达武陵源，求两车的速度各是多少？‎ ‎22．（本小题9分）‎ 如图，有两个动点分别从正方形的两个顶点同时出发，以相同速度分别沿边和移动，问：‎ ‎（1）在移动过程中，与的位置和大小有何关系？并给予证明．‎ ‎（2）若和相交点，图中有多少对相似三角形？请把它们写出来．‎ F D C E O B A ‎23．（本小题9分）‎ 我市今年初三体育考试结束后，从某县3000名参考学生中抽取了100名考生成绩进行统计分析（满分100分，记分均为整数），得到如图所示的频数分布直方图，请你根据图形完成下列问题：‎ ‎（1）本次抽样的样本容量是 ．‎ ‎（2）请补全频数分布直方图．‎ ‎（3）若80分以上（含80分）为优秀，请你据此．估算该县本次考试的优秀人数．‎ ‎39.5‎ ‎49.5‎ ‎59.5‎ ‎69.5‎ ‎79.5‎ ‎89.5‎ ‎100‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ 人数 分数 ‎2‎ ‎3‎ ‎5‎ ‎30‎ ‎20‎ ‎24．（本小题9分）‎ 有若干个数，第1个数记为，第2个数记为，第3个数记为，第个数记为，若，从第二个数起，每个数都等于1与前面那个数的差的倒数．‎ ‎（1）分别求出的值．‎ ‎（2）计算的值．‎ ‎25．（本小题12分）‎ 在平面直角坐标系中，已知，，且以为直径的圆交轴的正半轴于点，过点作圆的切线交轴于点．‎ ‎（1）求过三点的抛物线的解析式 ‎（2）求点的坐标 y x O C D B A ‎1‎ ‎2‎ ‎（3）设平行于轴的直线交抛物线于两点，问：是否存在以线段为直径的圆，恰好与轴相切？若存在，求出该圆的半径，若不存在，请说明理由？‎ 张家界市2009年初中毕业学业考试数学试卷答案 一、选择题 ‎1．B 2．A 3．B 4．A 5．C 6．D 7．C 8．A 二、填空题 ‎9． 10． 11． 12．‎ ‎13． 14． 15．16 16．‎ 三、解答题 ‎17．原式 3分 ‎ 4分 ‎ 5分 ‎ 6分 ‎18．解：‎ ‎ 2分 ‎，则 ‎ 4分 ‎ 5分 ‎ 6分 ‎19．解：原式 ‎ 2分 ‎ 3分 ‎ 4分 当时 ‎ ‎ 6分 A C B P OP xP yP ‎20．注：每问2分 ‎（3）‎ ‎21．解：设旅游客车速度为Km/h，则小车为Km/h 1分 ‎ 3分 解方程得 7分 经检验是方程的根，且合题意Km/时 8分 答：小车的平均速度为‎120Km/时 9分 ‎22．解：（1）在正方形中，，‎ ‎ 1分 ‎（SAS） 2分 ‎ 3分 ‎ 4分 在中，‎ ‎ 6分 ‎（2）有5对相似三角形 7分 ‎　　　　‎ ‎　　 9分 ‎23．（1）100 2分 ‎（2） 5分 ‎（3）‎ 该县优秀人数约为1800人 9分 ‎39.5‎ ‎49.5‎ ‎59.5‎ ‎69.5‎ ‎79.5‎ ‎89.5‎ ‎100‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ 人数 分数 ‎2‎ ‎3‎ ‎5‎ ‎30‎ ‎20‎ ‎40‎ ‎24．解：（1） 2分 ‎ 4分 ‎ 6分 ‎（2） 9分 ‎25．解：（1）令二次函数，则 ‎ 1分 ‎ 2分 过三点的抛物线的解析式为 4分 ‎（2）以为直径的圆圆心坐标为 ‎ 5分 为圆切线 6分 ‎ ‎ ‎ 8分 ‎ ‎ 坐标为 9分 ‎（3）存在 10分 抛物线对称轴为 设满足条件的圆的半径为，则的坐标为或 而点在抛物线上 ‎ ‎ 故在以为直径的圆，恰好与轴相切，该圆的半径为， 12分 注：解答题只要方法合理均可酌情给分