九年级数学上册 2422 直线和圆的位置关系教学 新版新人教版

申明敬告： 本站不保证该用户上传的文档完整性，不预览、不比对内容而直接下载产生的反悔问题本站不予受理。

文档介绍

九年级数学上册 2422 直线和圆的位置关系教学 新版新人教版

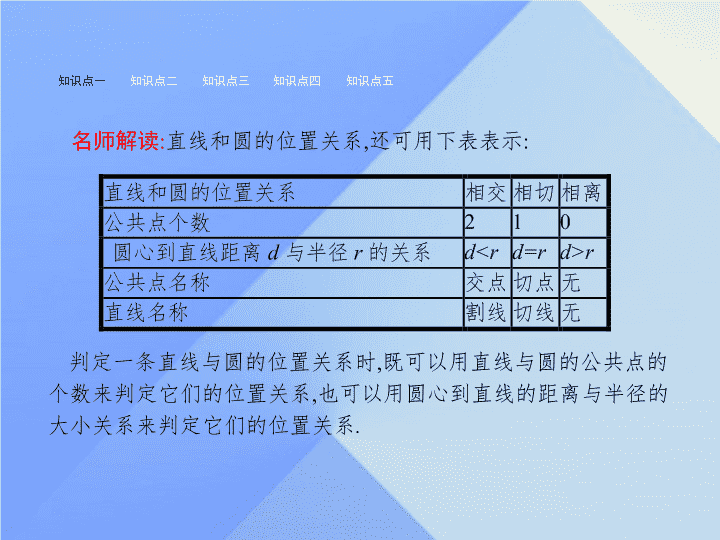
24.2.2 　直线和圆的位置关系 知识点一 知识点二 知识点三 知识点四 知识点五 知识点一 直线与圆的位置关系 直线和圆有两个公共点 , 这时我们就说这条直线和圆相交 , 这条直线叫做圆的割线 . 直线和圆只有一个公共点 , 这时我们就说这条直线和圆相切 , 这条直线叫做圆的切线 . 直线和圆没有公共点 , 这时我们说这条直线和圆相离 . 设 ☉ O 的半径为 r , 点 O 到直线 l 的距离为 d , 则直线 l 和 ☉ O 相交 ⇔ dr. 知识点一 知识点二 知识点三 知识点四 知识点五 名师解读 : 直线和圆的位置关系 , 还可用下表表示 : 判定一条直线与圆的位置关系时 , 既可以用直线与圆的公共点的个数来判定它们的位置关系 , 也可以用圆心到直线的距离与半径的大小关系来判定它们的位置关系 . 知识点一 知识点二 知识点三 知识点四 知识点五 例 1 　 如图 , △ ABC 中 , ∠ C= 90 ° , ∠ B= 60 ° , AO=x , O 在 AB 上 , 且 ☉ O 的半径为 1 . 问当 x 在什么范围内取值时 AC 与 ☉ O 相离、相切、相交 ? 分析 : 由三角形的内角和定理可求出 ∠ A 的大小 , 根据含 30 ° 角的直角三角形的性质即可得到 OD 和 AO 的关系 , (1) 若圆 O 与 AC 相离 , 则有 OD 大于 r , 列出关于 x 的不等式 , 求出不等式的解集即可得到 x 的范围 ; (2) 若圆 O 与 AC 相切 , 则有 OD=r , 求出 x 的值即可 ; (3) 若圆 O 与 AC 相交 , 则有 OD 小于 r , 列出关于 x 的不等式 , 求出不等式的解集即可得到 x 的范围 . 知识点一 知识点二 知识点三 知识点四 知识点五 知识点一 知识点二 知识点三 知识点四 知识点五 解答这类问题时 , 可以先画出草图 , 利用直线与圆的位置关系由圆心到直线的距离 d 与圆的半径 r 的大小关系来判断 . 知识点一 知识点二 知识点三 知识点四 知识点五 知识点二 切线的判定 经过半径的外端并且垂直于这条半径的直线是圆的切线 . 名师解读 : 切线的判定方法可以归纳为两种 : (1) 定义法 : 和圆有唯一公共点的直线是圆的切线或到圆心的距离等于圆的半径的直线是圆的切线 ; (2) 切线的判定定理 . 知识点一 知识点二 知识点三 知识点四 知识点五 例 2 　 如图 , 在等腰三角形 ABC 中 , AB=AC , O 为 AB 上一点 , 以 O 为圆心 , OB 长为半径的圆交 BC 于 D , DE ⊥ AC 交 AC 于 E. 求证 : DE 是 ☉ O 的切线 . 分析 : 连接 OD , 由 OB=OD , AB=AC , 可得到 ∠ ODB= ∠ C , 即 OD ∥ AC , 而 DE ⊥ AC , 即可得到 OD ⊥ DE , 从而得到 DE 是 ☉ O 的切线 . 知识点一 知识点二 知识点三 知识点四 知识点五 证明 : 如图所示 , 连接 OD , 则 OB=OD , ∴ ∠ OBD= ∠ ODB. 又 ∵ AB=AC , ∴ ∠ OBD= ∠ C. ∴ ∠ ODB= ∠ C. ∴ OD ∥ AC. 又 ∵ DE ⊥ AC , ∴ OD ⊥ DE. ∴ DE 是 ☉ O 的切线 . 知识点一 知识点二 知识点三 知识点四 知识点五 当已知直线过圆上一点 , 要证明它是圆的切线 , 则要连接圆心和这个点 , 证明这个连线与已知直线垂直即可 . 知识点一 知识点二 知识点三 知识点四 知识点五 知识点三 切线的性质 圆的切线垂直于过切点的半径 . 名师解读 : 切线的性质定理与判定定理互为逆定理 , 切线的判定定理是由 “ 垂直得切线 ” ; 而性质定理是由 “ 切线得垂直 ” . 当已知条件中有切线 , 而图形中没有经过切点的半径 ( 或直径 ) 时 , 通常作出经过切点的半径 , 这是解答这类问题的常规辅助线 . 知识点一 知识点二 知识点三 知识点四 知识点五 例 3 　 如图 , P 是 ☉ O 外一点 , PA 是 ☉ O 的切线 , A 为切点 , PO 与 ☉ O 相交于 B 点 , 已知 ∠ P= 28 ° , C 为 ☉ O 上一点 , 连接 CA , CB , 则 ∠ C 的度数为 ( 　　 ) 　　　　　 　　　　　　　　 A.28 ° B.62 ° C.31 ° D.56 ° 知识点一 知识点二 知识点三 知识点四 知识点五 知识点一 知识点二 知识点三 知识点四 知识点五 当题目中有圆的切点 , 而过切点的半径又没有时 , 一般作出这条半径 , 再利用切线的性质定理结合圆周角等其他知识来求解 . 知识点一 知识点二 知识点三 知识点四 知识点五 知识点四 切线长及其定理 切线长 : 经过圆外一点的圆的切线上 , 这点和切点之间线段的长 , 叫做这点到圆的切线长 . 定理 : 从圆外一点可以引圆的两条切线 , 它们的切线长相等 . 这一点和圆心的连线平分两条切线的夹角 . 名师解读 : 理解 “ 切线长 ” 时可以类比 “ 两点间的距离 ” , 切线长是数量 , 而不是图形 . 运用切线长定理可以得出角相等和线段相等 , 因此 , 在解答与两条切线有关的问题时 , 常常运用此定理找相等的角或线段 . 知识点一 知识点二 知识点三 知识点四 知识点五 例 4 　 如图 , PA , PB 分别切 ☉ O 于 A , B , PA= 10 cm, C 是劣弧 上的点 ( 不与点 A , B 重合 ), 过点 C 的切线分别交 PA , PB 于点 E , F. 则 △ PEF 的周长为 ( 　　 ) A.10 cm B.15 cm C.20 cm D.25 cm 知识点一 知识点二 知识点三 知识点四 知识点五 解析 : 由于 △ PEF 的三边都是变化的 , 而图形中有三条圆的切线 , 故易考虑到使用切线长定理进行转化 . ∵ PA , PB 分别切 ☉ O 于 A , B , ∴ PB=PA= 10 cm . ∵ EA 与 EC 为 ☉ O 的切线 , ∴ EA=EC , 同理得到 FC=FB , ∴ △ PEF 的周长 =PE+EF+PF=PE+EC+FC+PF=PE+EA+FB+PF=PA+PB= 10 + 10 = 20(cm) . 答案 : C 知识点一 知识点二 知识点三 知识点四 知识点五 解答本题关键是运用切线长定理得出 EC=AE , CF=FB , 最后把三角形的周长转化成两条切线长的和 . 知识点一 知识点二 知识点三 知识点四 知识点五 知识点五 内切圆及内心 内切圆 : 与三角形的三边都相切的圆叫做三角形的内切圆 . 内心 : 内切圆的圆心是三角形三条角平分线的交点 , 叫做三角形的内心 . 名师解读 : (1) 一个三角形有且只有一个内切圆 , 而一个圆的外切三角形有无数多个 . (2) 三角形的内心是三角形三个内角的平分线的交点 , 这点到三角形三边的距离相等 , 一定在三角形的内部 . 知识点一 知识点二 知识点三 知识点四 知识点五 例 5 　 如图 , ☉ O 是 Rt △ ABC 的内切圆 , D , E , F 分别为切点 , ∠ ACB= 90 ° , 则 ∠ EDF 的度数为 ( 　　 ) A.25 ° B.30 ° C.45 ° D.60 ° 知识点一 知识点二 知识点三 知识点四 知识点五 解析 : 由于 ∠ EDF 是圆周角 , 所以考虑构造出所对的弧所对的圆心角 , 又有切点 , 所以想到连接 OE , OF. ∵ ☉ O 是 Rt △ ABC 的内切圆 , D , E , F 分别为切点 , ∴ OE ⊥ BC , OF ⊥ AC. ∴ ∠ OEC= ∠ OFC= 90 ° . ∵ ∠ C= 90 ° , 由四边形的内角和得 ∠ EOF= 90 ° . ∴ ∠ EDF= ∠ EOF= 45 ° . 答案 : C 知识点一 知识点二 知识点三 知识点四 知识点五 解答这类问题的关键是构造出 ∠ EDF 所对应的圆心角 . 拓展点一 拓展点二 拓展点一 直线与圆的位置关系的灵活运用 例 1 　 如图所示 , 正方形的边长为 4, ☉ O 的半径为 1, 正方形中心 O 1 与圆心 O 在直线 l 上 , ☉ O 与 CD 边相切 , ☉ O 以 1 cm/s 的速度向左边运动 . (1) 当运动时间 t 在何数值范围时 ☉ O 与 CD 相交 ? (2) 当 t 为何值时 , ☉ O 与 AB 相切 ? 拓展点一 拓展点二 分析 : (1) 由 t= 0 或 t= 2 时 , ☉ O 与 CD 边相切 , 得出当 0
查看更多

相关文章

您可能关注的文档