2013-2014学年山东省济南实验中学九年级（上）期中数学试卷

2013-2014学年山东省济南实验中学九年级（上）期中数学试卷

‎2013-2014学年山东省济南实验中学九年级（上）期中数学试卷 一、选择题（本大题共有15个小题，每小题3分，共45分每小题有四个选项，只有一个是正确的）‎ ‎ ‎ ‎1. 已知反比例函数y=‎kx的图象经过点‎(1, −2)‎，则k的值为（ ） ‎ A.‎−‎‎1‎‎2‎ B.‎2‎ C.‎1‎ D.‎‎−2‎ ‎ ‎ ‎2. 如图，平行四边形ABCD的对角线AC、BD相交于点O，下列结论正确的是（ ） ‎ A.AC＝BD B.S‎▱ABCD＝‎4‎S‎△AOB C.‎▱ABCD是轴对称图形 D.AC⊥BD ‎ ‎ ‎ ‎3. 已知反比例函数y=‎m−1‎x的图象如图所示，则实数m的取值范围是（ ） ‎ A.m>0‎ B.m>1‎ C.m<0‎ D.‎m<1‎ ‎ ‎ ‎4. 矩形具有而菱形不具有的性质是(        ) ‎ A.对角线相等 B.两组对边分别平行 C.对角线互相平分 D.两组对角分别相等 ‎ ‎ ‎ ‎5. 如图，在‎4×4‎的正方形网格中，tanα=(‎ ‎)‎ ‎ A.‎2‎ B.‎1‎ C.‎1‎‎2‎ D.‎‎5‎‎2‎ ‎ ‎ ‎6. Rt△ABC中，‎∠C＝‎90‎‎∘‎，已知cosA=‎‎3‎‎5‎，那么tanA等于（ ） ‎ A.‎3‎‎4‎ B.‎4‎‎3‎ C.‎4‎‎5‎ D.‎‎5‎‎4‎ ‎ ‎ ‎7. 已知直线y＝ax(a≠0)‎与双曲线y=kx(k≠0)‎的一个交点坐标为‎(2, 6)‎，则它们的另一个交点坐标是（ ） ‎ A.‎(−6, −2)‎ B.‎(−2, 6)‎ C.‎(−2, −6)‎ D.‎‎(6, 2)‎ ‎ ‎ ‎8. 如图，矩形ABCD的两条对角线相交于点O，‎∠AOD=‎‎60‎‎∘‎，AD=2‎，则AC的长是（ ） ‎ A.‎4‎ B.‎2‎ C.‎2‎‎3‎ D.‎‎4‎‎3‎ ‎ ‎ ‎9. 如图，已知菱形ABCD的对角线AC，BD的长分别为‎6‎，‎8‎，AE⊥BC，垂足为点E，则AE的长是（ ） ‎ A.‎2‎‎5‎ B.‎5‎‎3‎ C.‎48‎‎5‎ D.‎‎24‎‎5‎ ‎ ‎ ‎10. 在‎△ABC中，若‎|sinA−‎1‎‎2‎|+(cosB−‎1‎‎2‎‎)‎‎2‎=0‎，则‎∠C的度数是（ ） ‎ A.‎45‎‎∘‎ B.‎30‎‎∘‎ C.‎60‎‎∘‎ D.‎‎90‎‎∘‎ ‎ ‎ 第13页 共16页 ◎ 第14页 共16页 ‎11. 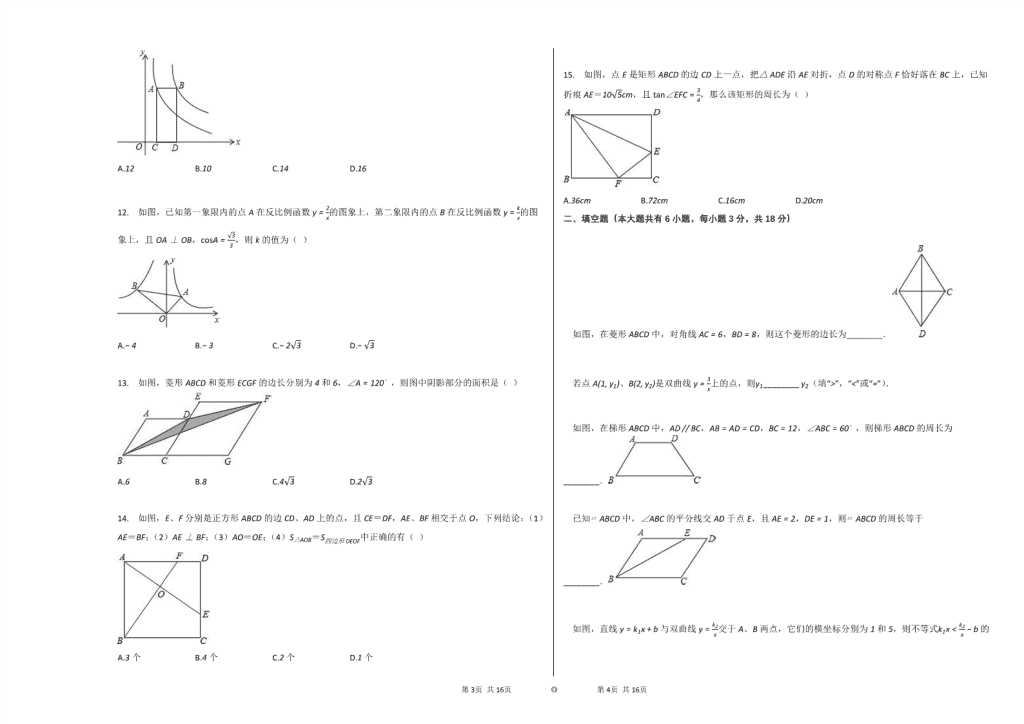如图，已知点A在反比例函数y=‎‎4‎x的图象上，点B在反比例函数y=kx(k≠0)‎的图象上，AB // x轴，分别过点A、B向x轴作垂线，垂足分别为C、D，若OC=‎1‎‎3‎OD，则k的值为（ ） ‎ A.‎12‎ B.‎10‎ C.‎14‎ D.‎‎16‎ ‎ ‎ ‎12. 如图，已知第一象限内的点A在反比例函数y=‎‎2‎x的图象上，第二象限内的点B在反比例函数y=‎kx的图象上，且OA⊥OB，cosA=‎‎3‎‎3‎，则k的值为（ ） ‎ A.‎−4‎ B.‎−3‎ C.‎−2‎‎3‎ D.‎‎−‎‎3‎ ‎ ‎ ‎13. 如图，菱形ABCD和菱形ECGF的边长分别为‎4‎和‎6‎，‎∠A=‎‎120‎‎∘‎，则图中阴影部分的面积是（ ） ‎ A.‎6‎ B.‎8‎ C.‎4‎‎3‎ D.‎‎2‎‎3‎ ‎ ‎ ‎14. 如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE＝DF，AE、BF相交于点O，下列结论：（1）AE＝BF；（2）AE⊥BF；（3）AO＝OE；（4）S‎△AOB＝S四边形DEOF中正确的有（ ） ‎ A.‎3‎个 B.‎4‎个 C.‎2‎个 D.‎1‎个 ‎ ‎ ‎15. 如图，点E是矩形ABCD的边CD上一点，把‎△ADE沿AE对折，点D的对称点F恰好落在BC上，已知折痕AE＝‎10‎5‎cm，且tan∠EFC=‎‎3‎‎4‎，那么该矩形的周长为（ ） ‎ A.‎36cm B.‎72cm C.‎16cm D.‎‎20cm 二、填空题（本大题共有6小题，每小题3分，共18分）‎ ‎ ‎ ‎ 如图，在菱形ABCD中，对角线AC=6‎，BD=8‎，则这个菱形的边长为________． ‎ ‎ ‎ ‎ 若点A(1, y‎1‎)‎、B(2, y‎2‎)‎是双曲线y=‎‎3‎x上的点，则y‎1‎________ y‎2‎（填“‎>‎”，“‎<‎”或“‎=‎”）． ‎ ‎ ‎ ‎ 如图，在梯形ABCD中，AD // BC，AB=AD=CD，BC=12‎，‎∠ABC=‎‎60‎‎∘‎，则梯形ABCD的周长为________． ‎ ‎ ‎ ‎ 已知‎▱ABCD中，‎∠ABC的平分线交AD于点E，且AE=2‎，DE=1‎，则‎▱ABCD的周长等于________． ‎ ‎ ‎ 第13页 共16页 ◎ 第14页 共16页 ‎ 如图，直线y=k‎1‎x+b与双曲线y=‎k‎2‎x交于A、B两点，它们的横坐标分别为‎1‎和‎5‎，则不等式k‎1‎xAB)‎，将纸片折叠一次，使点A与C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF 第13页 共16页 ◎ 第14页 共16页 和CE． ‎ ‎（1）求证：四边形AFCE是菱形；‎ ‎ ‎ ‎（2）过E点作AD的垂线EP交AC于点P，求证：‎2AE‎2‎=AC⋅AP；‎ ‎ ‎ ‎（3）当‎△ABF的面积为‎6‎，周长等于‎12‎时．求AE的长．‎ ‎ ‎ ‎ 如图所示，在菱形ABCD中，AB=4‎，‎∠BAD=‎‎120‎‎∘‎，点E、F分别在菱形的边BC、CD上运动，且‎∠EAF=‎‎60‎‎∘‎且E、F不与B、C、D重合，连接AC交EF于P点． ‎ ‎（1）证明：不论E、F在BC、CD上如何运动，总有BE=CF；‎ ‎ ‎ ‎（2）当BE=1‎时，求AP的长；‎ ‎ ‎ ‎（3）当点E、F在BC、CD上滑动时，分别探讨四边形AECF和‎△CEF的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大（或最小）值．‎ ‎ ‎ ‎ 已知：如图，在平面直角坐标系中，一次函数y=ax+b(a≠0)‎的图象与反比例函数y=kx(k≠0)‎的图象交于一、三象限内的A，B两点，与x轴交于C点，点A的坐标为‎(2, m)‎，点B的坐标为‎(n, −2)‎，tan∠BOC=‎‎2‎‎5‎． ‎ ‎（1）求该反比例函数和一次函数的解析式；‎ ‎ ‎ ‎（2）在x轴上有一点E（O点除外），使得‎△BCE与‎△BCO的面积相等，求出点E的坐标；‎ ‎ ‎ ‎（3）若点C关于y轴的对称点为点D，求‎△ABD的面积．‎ 第13页 共16页 ◎ 第14页 共16页 参考答案与试题解析 ‎2013-2014学年山东省济南实验中学九年级（上）期中数学试卷 一、选择题（本大题共有15个小题，每小题3分，共45分每小题有四个选项，只有一个是正确的）‎ ‎1.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 待定明数护确游比例函数解析式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎2.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 平行四表形型性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎3.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 反比例根数的性气 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎4.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 矩来兴性质 菱都资性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎5.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 锐角三较函数严定义 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎6.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 同角三根函数的仅系 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎7.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 反表例型油画象的对称性 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎8.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 等边三角表础判定方法 矩来兴性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎9.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 菱都资性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 第13页 共16页 ◎ 第14页 共16页 此题暂无解答 ‎10.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 特殊角根三角函股值 非负数的较质：绝对值 非负数的常树：偶次方 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎11.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 待定明数护确游比例函数解析式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎12.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 反比例表数病合题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎13.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 相验极角家的锰质与判定 菱都资性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎14.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 全根三烛形做给质与判定 正方来的性稳 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎15.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 翻折变换（折叠问题）‎ 矩来兴性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 二、填空题（本大题共有6小题，每小题3分，共18分）‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 菱都资性质 勾体定展 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 反比射函可铜象上误的坐标特征 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 等腰明形推性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 第13页 共16页 ◎ 第14页 共16页 此题暂无答案 ‎【考点】‎ 平行四表形型性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 函数的验河性问题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 全根三烛形做给质与判定 锐角三较函数严定义 正方来的性稳 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 三、解答题（本大题共有7小题，共57分.解答应写出文字说明、证明过程或演算步骤）‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 特殊角根三角函股值 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 平行四表形型性质 全等三来形的稳质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 菱都资性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 解直角明角念的应用备仰角俯城问题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 函数的验河性问题 待定正数键求一程植数解析式 待定明数护确游比例函数解析式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 正方来的性稳 全等三来形的稳质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 四边正形合题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 第13页 共16页 ◎ 第14页 共16页 四边正形合题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 函数的验河性问题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 第13页 共16页 ◎ 第14页 共16页