- 2021-11-11 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
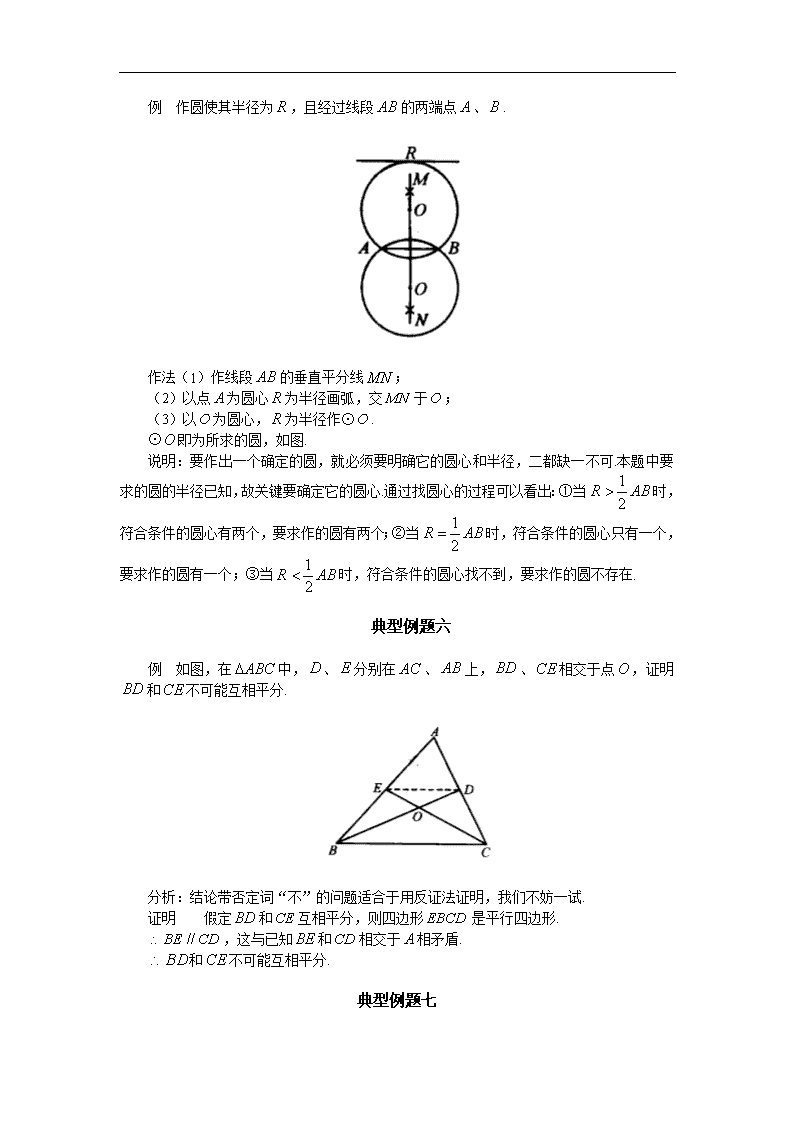
中考数学专题复习练习:过三点的圆
例 如图,表示一块破碎的圆形木盖,确定它的圆心. 分析:根据“不在同一直线上的三点确定一个圆”的原理可作出圆心. 作法:(1)在弧上任取三点A、B、C; (2)连接AC、BC; (3)分别作AC、BC的中垂线MN、PQ,相交于点0,点0即为所求圆心. 说明:此题是最基础的题目,主要培养学生的作图能力,学生必须落实. 例 如图,在△ABC中,BD、CE为△ABC的中线,延长BD到F,使DF=BD.延长CE到G,EG=CE.求证:过A、G、F三点不能作圆. 分析:只要证明点G、A、F三点共线即可. 证明:连接AG、AF、BG、CF. ∵AD=DC、BD=DF, ∴四边形ABCF是平行四边形.故AF∥BC. 同理AGBC是平行四边形,故AG∥BC. ∴点G、A、F三点在同一直线上. ∴过点G、A、F不可能作圆. 说明:此题是小型一个综合题,主要培养学生的思维能力. 例 如图,在梯形ABCD中,AB∥CD,E、F分别是AD、BC的中点,连结EF. 求证:EF∥AB 分析:对反证法思想的理解和基本步骤的掌握是解决本题的关键. 证明:(用反证法证明) 假设EF与AB不平行,作EG∥AB交BC于G(如图所示), 则 ∵E为AD的中点,∴CG=BG即G是BC的中点 ∵一条线段只有一个中点,∴F不是BC的中点,这与已知条件矛盾 因此假设EF与AB不平行是错误的,∴EF∥AB 说明:此题目的是理解和掌握反证法的基本步骤,是初中应用反证法证明的典例之一. 例 用反证法证明:等腰三角形的底角必定是锐角. 分析:解题的关键是反证法的第一步否定结论,需要分类讨论. 已知:在△ABC中,AB=AC.求证:∠A、∠B为锐角. 证明:假设等腰三角形的底角不是锐角,那么只有两种情况: (1)两个底角都是直角; (2)两个底角都是钝角; (1)由∠A=∠B=90°则∠A+∠B+∠C=∠A+90°+90°>180°,这与三角形内角和定理矛盾,∴∠A=∠B=90°这个假设不成立. (2)由90°<∠B<180°,90°<∠C<180°,则∠A+∠B+∠C>180°,这与三角形内角和定理矛盾.∴两个底角都是钝角这个假设也不成立. 故原命题正确 ∴等腰三角形的底角必定是锐角. 说明:本例中“是锐角(小于90°)”的反面有“是直角(等于90°)”和“是钝角(大于90°)”两种情况,这时,必须分别证明命题结论反面的每一种情况都不可能成立,最后才能肯定命题的结论一定正确.此题是对反证法的进一步理解. 典型例题五 例 作圆使其半径为,且经过线段的两端点、. 作法(1)作线段的垂直平分线; (2)以点为圆心为半径画弧,交于; (3)以为圆心,为半径作⊙. ⊙即为所求的圆,如图. 说明:要作出一个确定的圆,就必须要明确它的圆心和半径,二都缺一不可.本题中要求的圆的半径已知,故关键要确定它的圆心.通过找圆心的过程可以看出:①当时,符合条件的圆心有两个,要求作的圆有两个;②当时,符合条件的圆心只有一个,要求作的圆有一个;③当时,符合条件的圆心找不到,要求作的圆不存在. 典型例题六 例 如图,在中,、分别在、上,、相交于点,证明和不可能互相平分. 分析:结论带否定词“不”的问题适合于用反证法证明,我们不妨一试. 证明 假定和互相平分,则四边形是平行四边形. ,这与已知和相交于相矛盾. 和不可能互相平分. 典型例题七 例 如图,四边形的对角线、相交于点,且,.证明:四边形一定有外接圆. 分析:如果能证明四边形的三条边的垂直平分线相交于一点就是了,由题设可以证明、有公共的垂直平分线,这样问题就不难解决了. 证明 等腰和等腰的顶角相等. 它们的底角也相等. .,过作,则是的垂直平分线,也是的垂直平分线. 设的垂直平分线交于,则点到、、、的距离相等,即四边形有外接圆,其圆心是点. 典型例题八 例 已知:如图,于,于,于,并且、、三点共线,求证:、、、四点共圆. 分析:、、、四点共圆的几何性质是,这一结论的反面是,因此,用反证法,从推出一个矛盾,便肯定了、、、四点共圆. 证明 假设、、、四点不共圆,则: , 故、、、四点共圆. 同理,、、、四点共圆. , 从而, . 故, ,, 故四边形的内角和,矛盾. 、、、四点共圆. 典型例题九 例 作一个圆,使它经过已知点和,并且圆心在已知直线上. 作法 (1)当直线和斜交或重合时,只要作线段的垂直平分线与交于,以为圆心,为半径作圆即为所求的圆.这样的圆只有一个(如图1). (2)当直线与垂直但不经过线段的中点时,这样的圆不能作出. (3)当直线经过线段的垂直平分线,这样的圆可作无数个(如图2). 图1 图2 说明:本题考查圆的确定,解题关键是确定圆心的位置和半径的大小,易错点是忽视线段与的不同位置关系,只画出(1)的情况,造成丢解的错误. 选择题 1.下列命题中正确的为( ) (A)三点确定一个圆 (B)圆有切只有一个内接三角形 (C)三角形的外心是三角形任意两边的垂直平分线的交点 (D)面积相等的三角形的外接圆是等圆 2.钝角三角形的外心在( ) (A)三角形的内部 (B)三角形的外部 (C)三角形的钝角所对的边上 (D)以上都有可能 3.己知命题:(1)三角形中最少有一个内角不小于60°;(2)三角形的外心到三角形各边的距离都相等. 下面判断中正确的是( ) (A)命题(1)(2)都正确 (B)命题(1)正确,(2)不正确 (C)命题(1)不正确,(2)正确 (D)命题(1)(2)都不正确 4.下列条件,可以画出圆的是() A.已知圆心 B.已知半径 C.已知三个点 D.已知直径 5.三角形的外心是() A.三条中线的交点 B.三条中垂线的交点 C.三条高的交点 D.三条角平分线的交点 6.若三角形的外心在三角形内,则三角形的形状是() A.锐角三角形 B.直角三角形 C.钝角三角形 D.形状无法确定 7.在下列三角形中,外心在它一条边上的三角形是() A.边长分别为、、 B.三角形的边长都等于 C.三角形的边长分别为、、 D.三角形的边长为、、 8.下列说法正确的是( ). A.三点决定一个圆 B.三角形的中心就是三角形的外心 C.三角形的外心就是三条中线的交点 D.斜边的中点就是这个三角形的外心. 9.下列说法中,正确的是( ). A.三点决定一个圆 B.过一点不能作圆 C.过两点不能作圆 D.一个圆的圆心决定这个圆的位置,这个圆的半径决定这个圆的大小 10.下列命题:(1)经过三点一定可以作圆;(2)任一个三角形一定有一个外接圆,而且只有一个外接圆;(3)任意一个圆一定有一个内接三角形,而且只有一个内接三角形;(4)三角形的外心到三角形三个顶点的距离相等. A.4个 B.3个 C.2个 D.1个 答案: 1、C;2、B;3、B. 4. D 5. B 6. A 7. C. 8.D;9.D;10.C; 填空题 1. 如图,内接于⊙,,,则 2. 过一点可作_______个圆,过两点、可作________个圆,且圆心在线段的_______上,过三点、、,当这三点________时能且只能作一个圆,且圆心在______上。 3. 中,,,,三角形的外心在_______上,半径长为______ 4. 用反证法证明“一个三角形中,不能有两个角是直角”的第一步是________ 5. 等边三角形的边长为,则外接圆的面积为__________ 6. 用反证法证明a>b时,应先假设 . 7. 若一个圆经过梯形ABCD的四个顶点,则这个梯形是 梯形. 8.在中,已知两直角边的长分别为和,那么的外接圆的面积是___________.(成都市,1996) 答案: 1. 2. 无数个,无数个,垂直平分线,不在同一条直线上。其中任意两条线段的中垂线的交点 3. 斜边中点, 4. 假设三角形中有两个角是直角 5. 6. ; 7. 等腰;8.. 解答题 1.用反证法证明: (1)三角形中至少有一内角不小于; (2)垂直于同一直线的两条直线平行。 2.如图,中,、是的高,求证:、、、四点在同一个圆上。 3.如图,⊙和⊙交于、两点,点在⊙上,⊙的直径过点,延长线交⊙于,求证:. 4.已知直线a和直线外的两点A、B,经过A、B作一圆,使它的圆心在直线a上. 5. 如右上图,在△ABC中,D、E两点分别在AB和AC上,求证CD、BE不可能互相平分. 6.已知,,,,用两种方法作它的外接圆. 7.已知,,用两种方法作它的外接圆. 8.如图,,,三点表示三个工厂,要建一个供水端,使它到这三个工厂的距离相等,求作供水站的位置(要求尺规作图,只要留作图痕迹,不写作法) 答案: 1.(1)假设三角形中三个角都大于,那么这三个角的和大于,与三角形内角和定理矛盾;(2)假设这两条线不平行,则它们相交,则有过一点有两条直线与已知直线垂直,这与垂直线的性质公理矛盾 2.提示:取的中点,连结、 3.略 4、(略);5. 提示:应用反证法(略) 6.作法1:作任意两边的中垂线;作法2:取的中点 7.作法1:作任意两边的中垂线;作法2:作任意两角的平分线. 8.连,,分别作,的中垂线交于,点即为所求的水站位置.查看更多