2020中考数学三轮复习——二次函数压轴题 练习

2020中考数学三轮复习——二次函数压轴题 练习

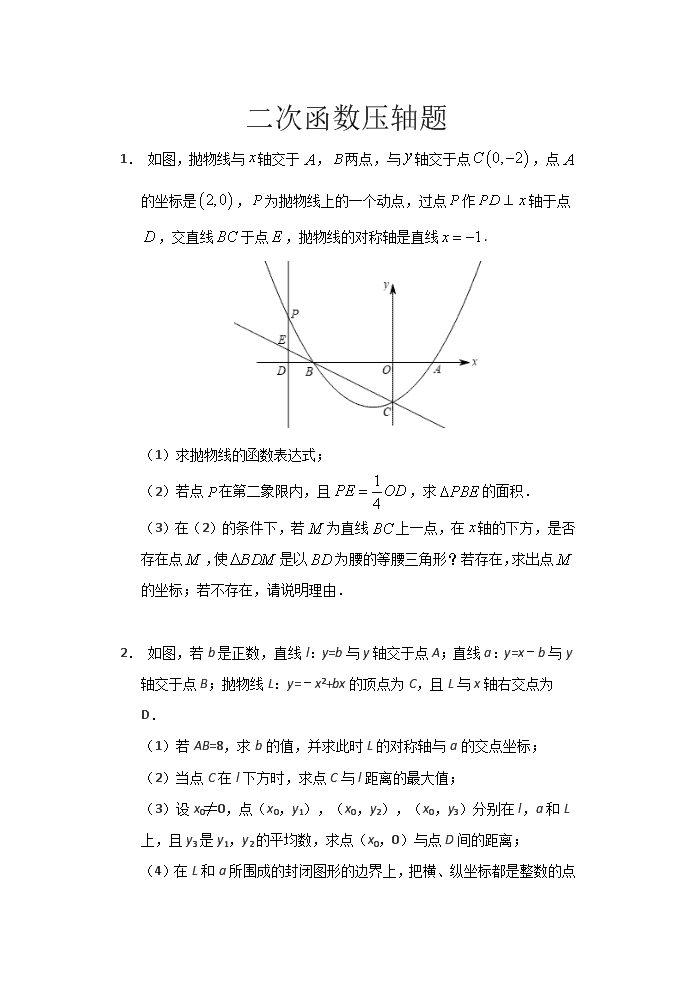
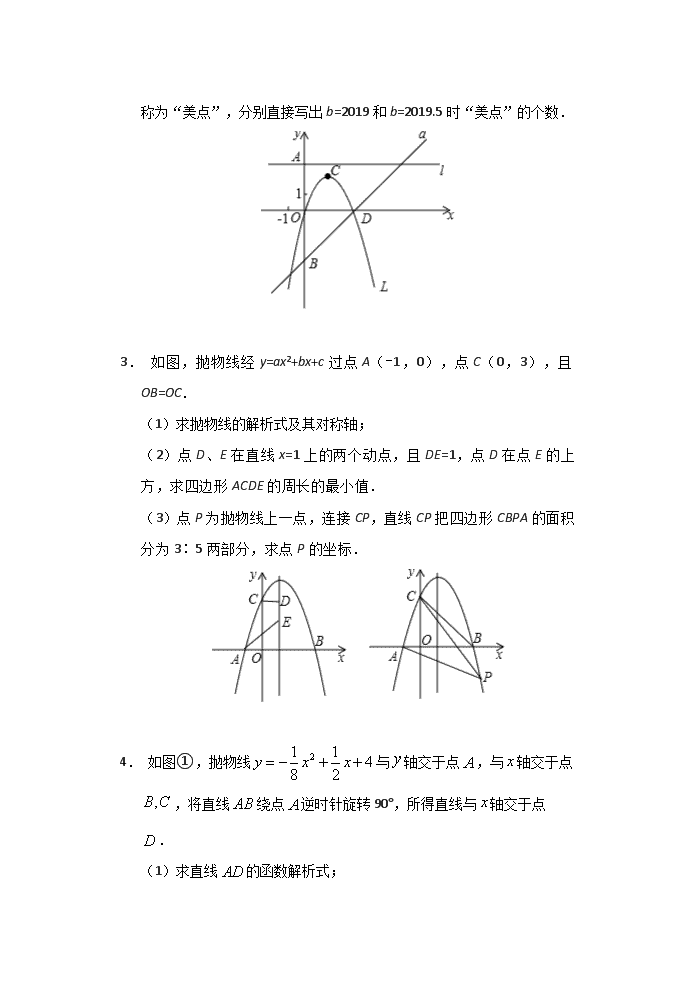
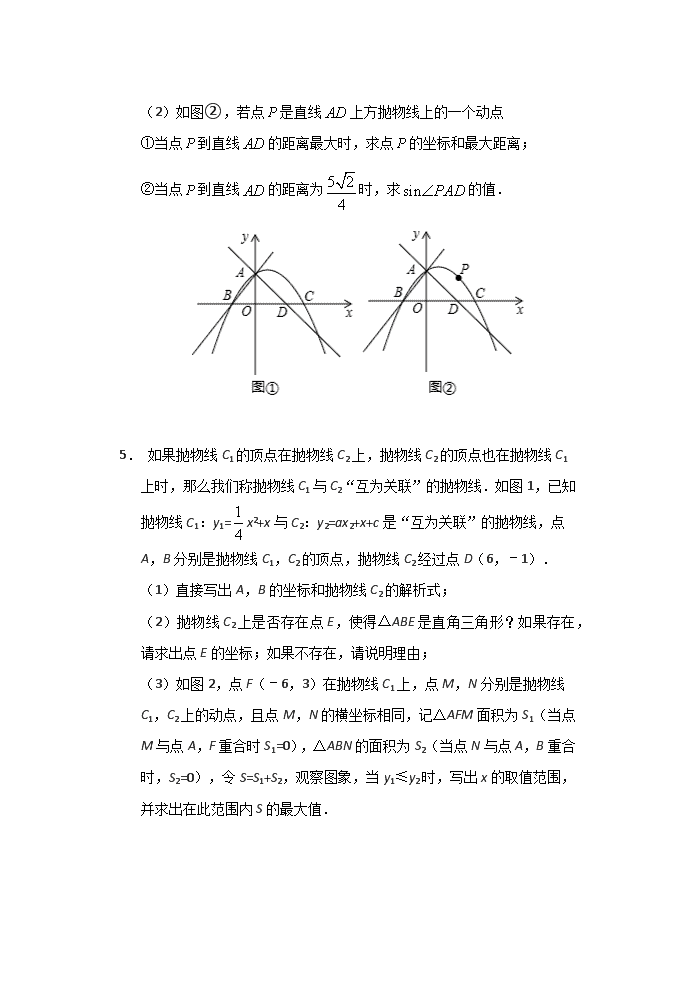
二次函数压轴题 ‎1． 如图，抛物线与轴交于，两点，与轴交于点，点的坐标是，为抛物线上的一个动点，过点作轴于点，交直线于点，抛物线的对称轴是直线.‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）若点在第二象限内，且，求的面积．‎ ‎（3）在（2）的条件下，若为直线上一点，在轴的下方，是否存在点，使是以为腰的等腰三角形？若存在，求出点的坐标；若不存在，请说明理由．‎ ‎ ‎ ‎2． 如图，若b是正数，直线l：y=b与y轴交于点A；直线a：y=x–b与y轴交于点B；抛物线L：y=–x2+bx的顶点为C，且L与x轴右交点为D．‎ ‎（1）若AB=8，求b的值，并求此时L的对称轴与a的交点坐标；‎ ‎（2）当点C在l下方时，求点C与l距离的最大值；‎ ‎（3）设x0≠0，点（x0，y1），（x0，y2），（x0，y3）分别在l，a和L上，且y3是y1，y2的平均数，求点（x0，0）与点D间的距离；‎ ‎（4）在L和a 所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出b=2019和b=2019.5时“美点”的个数．‎ ‎ ‎ ‎3． 如图，抛物线经y=ax2+bx+c过点A（-1，0），点C（0，3），且OB=OC．‎ ‎（1）求抛物线的解析式及其对称轴；‎ ‎（2）点D、E在直线x=1上的两个动点，且DE=1，点D在点E的上方，求四边形ACDE的周长的最小值．‎ ‎（3）点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为3∶5两部分，求点P的坐标．‎ ‎ ‎ ‎4． 如图①，抛物线与轴交于点，与轴交于点，将直线绕点逆时针旋转90°，所得直线与轴交于点．‎ ‎（1）求直线的函数解析式；‎ ‎（2）如图②，若点是直线上方抛物线上的一个动点 ‎①当点到直线的距离最大时，求点的坐标和最大距离；‎ ‎②当点到直线的距离为时，求的值．‎ ‎ ‎ ‎5． 如果抛物线C1的顶点在拋物线C2上，抛物线C2的顶点也在拋物线C1上时，那么我们称抛物线C1与C2“互为关联”的抛物线．如图1，已知抛物线C1：y1=x2+x与C2：y2=ax2+x+c是“互为关联”的拋物线，点A，B分别是抛物线C1，C2的顶点，抛物线C2经过点D（6，–1）．‎ ‎（1）直接写出A，B的坐标和抛物线C2的解析式；‎ ‎（2）抛物线C2上是否存在点E，使得△ABE是直角三角形？如果存在，请求出点E的坐标；如果不存在，请说明理由；‎ ‎（3）如图2，点F（–6，3）在抛物线C1上，点M，N分别是抛物线C1，C2上的动点，且点M，N的横坐标相同，记△AFM面积为S1（当点M与点A，F重合时S1=0），△ABN的面积为S2（当点N与点A，B重合时，S2=0），令S=S1+S2，观察图象，当y1≤y2时，写出x的取值范围，并求出在此范围内S的最大值．‎ ‎ ‎ ‎6． 已知抛物线经过和两点，与轴交于点，点为第一象限抛物线上一动点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）如图1，连接，交于点，当时，求出点的坐标；‎ ‎（3）如图2，点的坐标为，点为轴正半轴上一点，，连接，是否存在点，使？若存在，请求出点的坐标；若不存在，请说明理由．‎ ‎ ‎ ‎7． 综合与探究 如图，抛物线经过点A（–2，0），B（4，0）两点，与轴交于点C，点D是抛物线上一个动点，设点D的横坐标为 ‎.连接AC，BC，DB，DC.‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）△BCD的面积等于△AOC的面积的时，求的值；‎ ‎（3）在（2）的条件下，若点M是轴上的一个动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形，若存在，请直接写出点M的坐标；若不存在，请说明理由.‎ ‎ ‎ 答案 ‎1． （1）点的坐标是，抛物线的对称轴是直线，则点，‎ 所以设函数的表达式为：，‎ 将点C（0，–2）代入得：，解得：，‎ 故抛物线的表达式为：；‎ ‎（2）设直线BC的解析式为y=mx+n，‎ 将点（–4，0）、（0，–2）分别代入得，解得：，‎ 所以直线的表达式为：，‎ 设点，则OD=–x，点，点，‎ ‎∴PE=，‎ ‎∵，∴=，‎ 解得：或x=–5（舍去），‎ ‎∴点，‎ ‎∴PE=，BD=–4–（–5）=1，‎ ‎∴；‎ ‎（3）由题意得：在x轴下方，是以为腰的等腰三角形，只存在：的情况，∴BM=BD=1，‎ ‎∵（–4，0）、（0，–2），∴OB=4，OC=2，‎ ‎∵∠BOC=90°，∴BC==，‎ ‎∴，‎ 设M的坐标为（xM，yM），‎ 则，‎ 则，‎ 故点.‎ ‎2． （1）当x=0吋，y=x﹣b=﹣b，∴B（0，﹣b），‎ ‎∵AB=8，而A（0，b），∴b﹣（﹣b）=8，∴b=4．‎ ‎∴L：y=﹣x2+4x，∴L的对称轴x=2，‎ 当x=2时，y=x﹣4=﹣2，‎ ‎∴L的对称轴与a的交点为（2，﹣2）；‎ ‎（2）∵y=﹣（x﹣）2+，∴L的顶点C（，），‎ ‎∵点C在l下方，∴C与l的距离为b﹣=﹣（b﹣2）2+1≤1，‎ ‎∴点C与l距离的最大值为1；‎ ‎（3）由題意得，即y1+y2=2y3，‎ 得b+x0﹣b=2（﹣x02+bx0），‎ 解得x0=0或x0=b﹣．但x0≠0，取x0=b﹣，‎ 对于L，当y=0时，0=﹣x2+bx，即0=﹣x（x﹣b），解得x1=0，x2=b，‎ ‎∵b＞0，∴右交点D（b，0）．‎ ‎∴点（x0，0）与点D间的距离为b﹣（b﹣）=.‎ ‎（4）①当b=2019时，抛物线解析式L：y=﹣x2+2019x，‎ 直线解析式a：y=x﹣2019，‎ 联立上述两个解析式可得：x1=﹣1，x2=2019，‎ ‎∴可知每一个整数x的值 都对应的一个整数y值，且﹣1和2019之间（包括﹣1和﹣2019），共有2021个整数；‎ ‎∵另外要知道所围成的封闭图形边界分两部分：线段和抛物线，‎ ‎∴线段和抛物线上各有2021个整数点，∴总计4042个点，‎ ‎∵这两段图象交点有2个点重复重复，∴美点”的个数：4042﹣2=4040（个）；‎ ‎②当b=2019.5时，‎ 抛物线解析式L：y=﹣x2+2019.5x，‎ 直线解析式a：y=x﹣2019.5，‎ 联立上述两个解析式可得：x1=﹣1，x2=2019.5，‎ ‎∴当x取整数时，在一次函数y=x﹣2019.5上，y取不到整数值，因此在该图象上“美点”为0，‎ 在二次函数y=x+2019.5x图象上，当x为偶数时，函数值y可取整数，‎ 可知﹣1到2019.5之间有1009个偶数，并且在﹣1和2019.5之间还有整数0，验证后可知0也符合，‎ 条件，因此“美点”共有1010个．‎ 故b=2019时“美点”的个数为4040个，b=2019.5时“美点”的个数为1010个．‎ ‎3． （1）∵OB=OC，‎ ‎∴点B（3，0），‎ 则抛物线的表达式为：y=a（x+1）（x-3）=a（x2-2x-3）=ax2-2ax-3a，‎ 故-3a=3，解得：a=-1，‎ 故抛物线的表达式为：y=-x2+2x+3，对称轴为x=1．‎ ‎（2）ACDE的周长=AC+DE+CD+AE，其中AC、DE=1是常数，‎ 故CD+AE最小时，周长最小，‎ 取点C关于函数对称点C（2，3），则CD=C′D，‎ 取点A′（-1，1），则A′D=AE，‎ 故：CD+AE=A′D+DC′，则当A′、D、C′三点共线时，CD+AE=A′D+DC′最小，周长也最小，‎ 四边形ACDE的周长的最小值=AC+DE+CD+AEA′D+DC′A′C′．‎ ‎（3）如图，设直线CP交x轴于点E，‎ 直线CP把四边形CBPA的面积分为3∶5两部分，‎ 又∵S△PCB∶S△PCAEB×（yC-yP）∶AE×（yC-yP）=BE∶AE，‎ 则BE∶AE=3∶5或5∶3，‎ 则AE或，‎ 即：点E的坐标为（，0）或（，0），‎ 将点E、C的坐标代入一次函数表达式：y=kx+3，‎ 解得：k=-6或-2，‎ 故直线CP的表达式为：y=-2x+3或y=-6x+3，‎ 联立并解得：x=4或8（不合题意值已舍去），‎ 故点P的坐标为（4，-5）或（8，-45）．‎ ‎4． （1）当时，则点的坐标为，‎ 当时，，解得，，则点的坐标为，点的坐标为，‎ ‎∴，∴，‎ ‎∵将直线绕点逆时针旋转得到直线，‎ ‎∴，∴，‎ ‎∴，∴，∴点的坐标为，‎ 设直线的函数解析式为 ‎，得，‎ 即直线的函数解析式为；‎ ‎（2）作轴交直线于点，如图①所示，‎ 设点的坐标为，则点的坐标为，‎ ‎∴，‎ ‎∴轴，‎ ‎∴轴，‎ ‎∴，‎ 作于点，则，‎ ‎∴，‎ ‎∴当时，取得最大值，此时点P的坐标为，‎ 即当点到直线的距离最大时，点的坐标是，最大距离是；‎ ‎②当点到直线的距离为时，如图②所示，‎ 则，解得：，‎ 则的坐标为，的坐标为，‎ 当的坐标为，则，∴；‎ 当的坐标为，则，‎ ‎∴；‎ 由上可得，的值是或．‎ ‎5． （1）C1顶点在C2上，C2顶点也在C1上，‎ 由抛物线C1：y1=x2+x可得A（–2，–1），‎ 将A（–2，–1），D（6，–1）代入y2=ax2+x+c 得，解得 ，‎ ‎∴y2=–x2+x+2，∴B（2，3）；‎ ‎（2）易得直线AB的解析式：y=x+1，‎ ‎①若B为直角的顶点，BE⊥AB，kBE•kAB=–1，‎ ‎∴kBE=–1，则直线BE的解析式为y=–x+5．‎ 联立，‎ 解得或，此时E（6，–1）；‎ ‎②若A为直角顶点，AE⊥AB，kAE•kAB=–1，‎ ‎∴kAE=–1，则直线AE的解析式为y=–x–3，‎ 联立，‎ 解得或，‎ 此时E（10，–13）；‎ ‎③若E为直角顶点，设E（m，–m2+m+2）‎ 由AE⊥BE得kBE•kAE=–1，‎ 即，‎ 解得m=2或–2（不符合题意均舍去），‎ ‎∴存在，∴E（6，–1）或E（10，–13）；‎ ‎（3）∵y1≤y2，观察图形可得：x的取值范围为–2≤x≤2，‎ 设M（t，t2+t），N（t，−t2+t+2），且–2≤t≤2，‎ 易求直线AF的解析式：y=–x–3，‎ 过M作x轴的平行线MQ交AF于Q，‎ 由yQ=yM，得Q（t2−t−3，t2+t），‎ S1=|QM|•|yF–yA|=t2+4t+6，‎ 设AB交MN于点P，易知P坐标为（t，t+1），‎ S2=|PN|•|xA–xB|=2–t2，‎ S=S1+S2=4t+8，‎ 当t=2时，S的最大值为16．‎ ‎6． （1）将和代入得：‎ ‎，‎ 解得：，‎ ‎∴抛物线的解析式为：．‎ ‎（2）如图，作轴，垂足为，‎ ‎∵，‎ ‎∴，，‎ ‎∵，‎ ‎∴，‎ ‎∵，，‎ ‎∴，‎ ‎∴，，‎ ‎∴，‎ ‎∴直线为：，‎ 由得：．‎ ‎（3）设交轴于点，如图，‎ ‎∵，，‎ ‎∴，‎ ‎∵，‎ ‎∴，‎ ‎∴，‎ ‎∴，‎ ‎∵，‎ ‎∴，‎ ‎∴，‎ ‎∴直线为：，‎ 由得：，，‎ ‎∵点在第一象限，‎ ‎∴．‎ ‎7． （1）抛物线经过点A（–2，0），B（4，0），‎ ‎∴，解得，‎ ‎∴抛物线的函数表达式为；‎ ‎（2）作直线DE⊥轴于点E，交BC于点G，作CF⊥DE，垂足为F，‎ ‎∵点A的坐标为（–2，0），∴OA=2，‎ 由，得，∴点C的坐标为（0，6），∴OC=6，‎ ‎∴S△OAC=，‎ ‎∵S△BCD=S△AOC，∴S△BCD=，‎ 设直线BC的函数表达式为，‎ 由B，C两点的坐标得，解得，‎ ‎∴直线BC的函数表达式为，‎ ‎∴点G的坐标为，‎ ‎∴，‎ ‎∵点B的坐标为（4，0），∴OB=4，‎ ‎∵S△BCD=S△CDG+S△BDG=‎ ‎，‎ ‎∴S△BCD=，‎ ‎∴，‎ 解得（舍），，‎ ‎∴的值为3；‎ ‎（3）存在，如下图所示，以BD为边或者以BD为对角线进行平行四边形的构图，‎ 以BD为边时，有3种情况，‎ ‎∵D点坐标为，∴点N点纵坐标为±，‎ 当点N的纵坐标为时，如点N2，‎ 此时，解得：（舍），‎ ‎∴，∴；‎ 当点N的纵坐标为时，如点N3，N4，‎ 此时，解得：‎ ‎∴，，‎ ‎∴，；‎ 以BD为对角线时，有1种情况，此时N1点与N2点重合，‎ ‎∵，D（3，），‎ ‎∴N1D=4，‎ ‎∴BM1=N1D=4，‎ ‎∴OM1=OB+BM1=8，‎ ‎∴M1（8，0），‎ 综上，点M的坐标为：.‎