九年级数学上册第24章解直角三角形24-4解直角三角形第2课时俯角和仰角的问题教案新版华东师大版

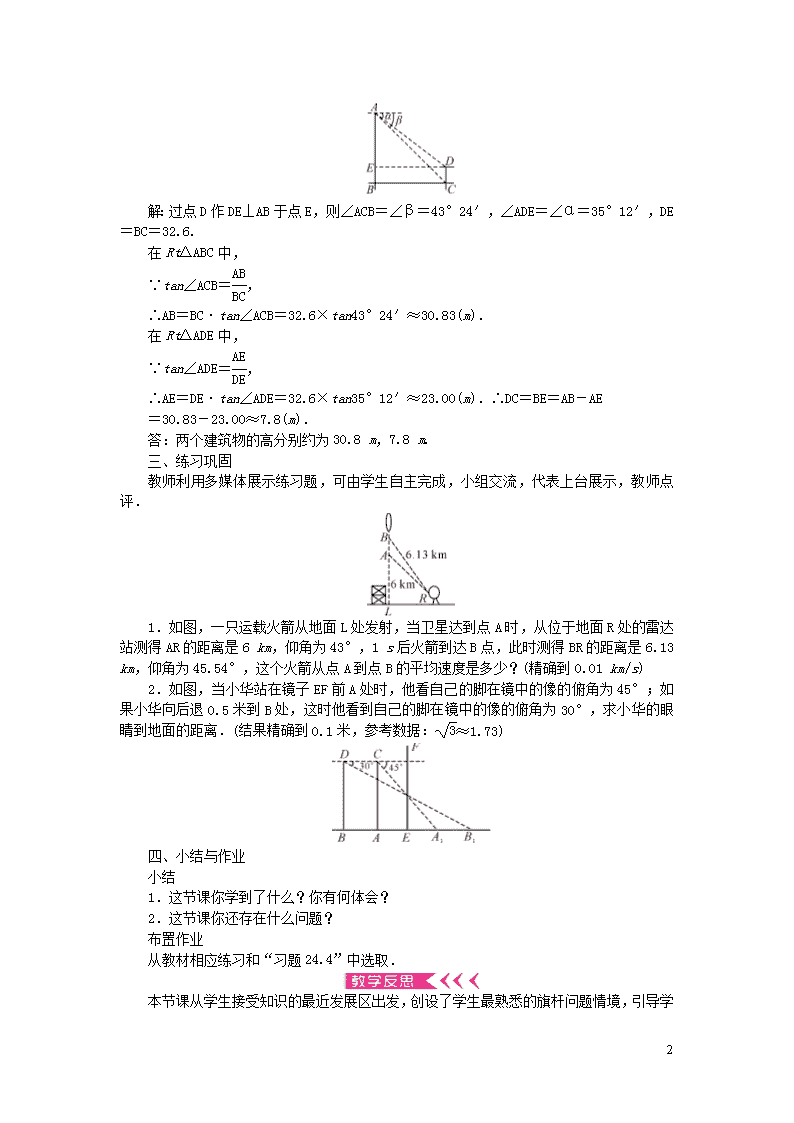
九年级数学上册第24章解直角三角形24-4解直角三角形第2课时俯角和仰角的问题教案新版华东师大版

第2课时　俯角和仰角的问题 ‎1．理解仰角、俯角的含义，准确运用这些概念来解决一些实际问题．‎ ‎2．培养学生将实际问题抽象成数学模型并进行解释与应用的能力．‎ 重点 理解仰角和俯角的概念．‎ 难点 能解与直角三角形有关的实际问题．‎ 一、情境引入 教师展示课件，引出问题．‎ 如图，为了测量旗杆的高度BC，小明站在离旗杆10米的A处，用高1.50米的测角仪DA测得旗杆顶端C的仰角α＝52°，然后他很快就算出旗杆BC的高度了．(精确到0.1米)‎ 你知道小明是怎样算出的吗？‎ 二、探究新知 教师结合展示的引例，结合图片，引导学生观察，分析，归纳仰角、俯角的概念．‎ 想要解决刚才的问题，我们先来了解仰角、俯角的概念．‎ 现在我们可以来看一看小明是怎样算出来的．‎ ‎【分析】在Rt△CDE中，已知一个角和一条边，利用解直角三角形的知识即可求出CE的长，从而求出CB的长．‎ 解：在Rt△CDE中，‎ ‎∵CE＝DE·tanα＝AB·tanα＝10×tan52°≈12.80，‎ ‎∴BC＝BE＋CE＝DA＋CE≈1.50＋12.80＝14.3(米)．‎ 答：旗杆的高度约为14.3米．‎ 教师再展示例题，引导学生思考、分析，关键是构造直角三角形，分清楚角所在的直角三角形，然后将实际问题转化为几何问题解决．‎ 例　如图，两建筑物的水平距离为32.6 m，从点A测得点D的俯角α为35°12′，测得点C的俯角β为43°24′，求这两个建筑物的高．(精确到0.1 m)‎ 3‎ 解：过点D作DE⊥AB于点E，则∠ACB＝∠β＝43°24′，∠ADE＝∠α＝35°12′，DE＝BC＝32.6.‎ 在Rt△ABC中，‎ ‎∵tan∠ACB＝，‎ ‎∴AB＝BC·tan∠ACB＝32.6×tan43°24′≈30.83(m)．‎ 在Rt△ADE中，‎ ‎∵tan∠ADE＝，‎ ‎∴AE＝DE·tan∠ADE＝32.6×tan35°12′≈23.00(m)．∴DC＝BE＝AB－AE ‎＝30.83－23.00≈7.8(m)．‎ 答：两个建筑物的高分别约为30.8 m，7.8 m.‎ 三、练习巩固 教师利用多媒体展示练习题，可由学生自主完成，小组交流，代表上台展示，教师点评．‎ ‎1．如图，一只运载火箭从地面L处发射，当卫星达到点A时，从位于地面R处的雷达站测得AR的距离是6 km，仰角为43°，1 s后火箭到达B点，此时测得BR的距离是6.13 km，仰角为45.54°，这个火箭从点A到点B的平均速度是多少？(精确到0.01 km/s)‎ ‎2．如图，当小华站在镜子EF前A处时，他看自己的脚在镜中的像的俯角为45°；如果小华向后退0.5米到B处，这时他看到自己的脚在镜中的像的俯角为30°，求小华的眼睛到地面的距离．(结果精确到0.1米，参考数据：≈1.73)‎ 四、小结与作业 小结 ‎1．这节课你学到了什么？你有何体会？‎ ‎2．这节课你还存在什么问题？‎ 布置作业 从教材相应练习和“习题24.4”中选取．‎ 本节课从学生接受知识的最近发展区出发 3‎ ‎，创设了学生最熟悉的旗杆问题情境，引导学生发现问题、分析问题．在探索活动中，学生自主探索知识，逐步把生活实际问题抽象成数学模型并进行解释与应用，养成交流与合作的良好习惯．让学生在学习过程中感受到成功的喜悦，产生后继学习的激情，增强学数学的信心．‎ 3‎