2006年上海市高考数学试卷（理科）【附答案、word版本，可再编辑；B4纸型两栏】

2006年上海市高考数学试卷（理科）【附答案、word版本，可再编辑；B4纸型两栏】

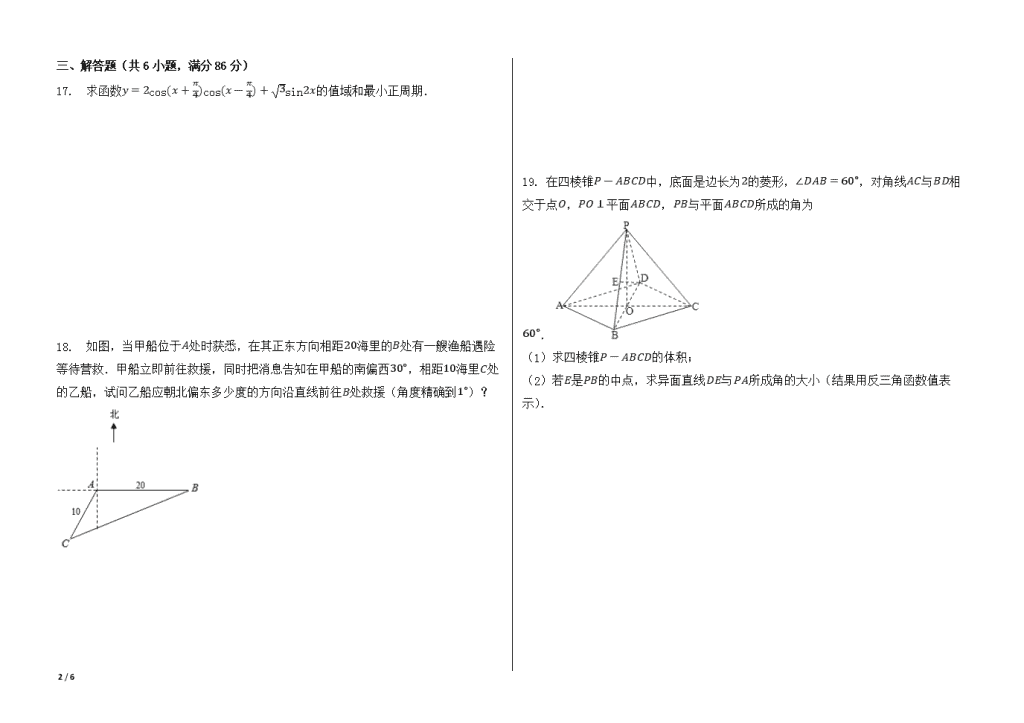
‎2006年上海市高考数学试卷（理科）‎ 一、填空题（共12小题，每小题4分，满分48分）‎ ‎1. 已知集合A＝‎{-1, 3, 2m-1}‎，集合B＝‎{3, m‎2‎}‎．若B⊆A，则实数m＝________．‎ ‎2. 已知圆x‎2‎‎-4x-4+y‎2‎=0‎的圆心是点P，则点P到直线x-y-1=0‎的距离是________．‎ ‎3. 若函数f(x)=ax(a>0‎，且a≠1)‎的反函数的图象过点‎(2, -1)‎，则a=‎________．‎ ‎4. 计算：limn→∞‎Cn‎3‎n‎3‎‎+1‎‎=‎________；‎ ‎5. 若复数z同时满足z-z‎¯‎=2i，z‎¯‎‎=iz（i为虚数单位），则z=‎________；‎ ‎6. 如果cosα=‎‎1‎‎5‎，且α是第四象限的角，那么cos(α+π‎2‎)=‎________．‎ ‎7. 已知椭圆中心在原点，一个焦点为F(-2‎3‎, 0)‎，且长轴长是短轴长的‎2‎倍，则该椭圆的标准方程是________．‎ ‎8. 在极坐标系中，O是极点，设点A(4, π‎3‎)‎，B(5, -‎5π‎6‎)‎，则‎△OAB的面积是________．‎ ‎9. 两部不同的长篇小说各由第一、二、三、四卷组成，每卷‎1‎本，共‎8‎本．将它们任意地排成一排，左边‎4‎本恰好都属于同一部小说的概率是________（结果用分数表示）．‎ ‎10. 如果一条直线与一个平面垂直，那么，称此直线与平面构成一个“正交线面对”．在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是________.‎ ‎11. 若曲线y‎2‎‎=|x|+1‎与直线y=kx+b没有公共点，则k、b分别应满足的条件是________．‎ ‎12. 三个同学对问题“关于x的不等式x‎2‎‎+25+|x‎3‎-5x‎2‎|≥ax在‎[1, 12]‎上恒成立，求实数a的取值范围”提出各自的解题思路．‎ 甲说：“只须不等式左边的最小值不小于右边的最大值”．‎ 乙说：“把不等式变形为左边含变量x的函数，右边仅含常数，求函数的最值”．‎ 丙说：“把不等式两边看成关于x的函数，作出函数图象”．‎ 参考上述解题思路，你认为他们所讨论的问题的正确结论，即a的取值范围是________．‎ 二、选择题（共4小题，每小题4分，满分16分）‎ ‎13. 如图，在平行四边形ABCD中，下列结论中错误的是‎(        )‎ A.AB‎→‎‎=‎DC‎→‎ B.‎AD‎→‎‎+AB‎→‎=‎AC‎→‎ C.AB‎→‎‎-AD‎→‎=‎BD‎→‎ D.‎AD‎→‎‎+CB‎→‎=‎‎0‎‎→‎ ‎14. 若空间中有四个点，则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的（ ）‎ A.充分非必要条件 B.必要非充分条件 C.充要条件 D.非充分非必要条件 ‎15. 若关于x的不等式‎(1+k‎2‎)x≤k‎4‎+4‎的解集是M，则对任意实常数k，总有（ ）‎ A.‎2∈M，‎0∈M B.‎2∉M，‎0∉M C.‎2∈M，‎0∉M D.‎2∉M，‎‎0∈M ‎16. 如图，平面中两条直线l‎1‎和l‎2‎相交于点O，对于平面上任意一点M，若p、q分别是M到直线l‎1‎和l‎2‎的距离，则称有序非负实数对‎(p, q)‎是点M的“距离坐标”．已知常数p≥0‎，q≥0‎，给出下列命题：‎ ‎①若p=q=0‎，则“距离坐标”为‎(0, 0)‎的点有且仅有‎1‎个；‎ ‎②若pq=0‎，且p+q≠0‎，则“距离坐标”为‎(p, q)‎的点有且仅有‎2‎个；‎ ‎③若pq≠0‎，则“距离坐标”为‎(p, q)‎的点有且仅有‎4‎个．‎ 上述命题中，正确命题的个数是（ ）‎ A.‎0‎ B.‎1‎ C.‎2‎ D.‎‎3‎ ‎ 6 / 6‎ 三、解答题（共6小题，满分86分）‎ ‎17. 求函数y=2cos(x+π‎4‎)cos(x-π‎4‎)+‎3‎sin2x的值域和最小正周期．‎ ‎18. 如图，当甲船位于A处时获悉，在其正东方向相距‎20‎海里的B处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西‎30‎‎∘‎，相距‎10‎海里C处的乙船，试问乙船应朝北偏东多少度的方向沿直线前往B处救援（角度精确到‎1‎‎∘‎）？‎ ‎19. 在四棱锥P-ABCD中，底面是边长为‎2‎的菱形，‎∠DAB=‎‎60‎‎∘‎，对角线AC与BD相交于点O，PO⊥‎平面ABCD，PB与平面ABCD所成的角为‎60‎‎∘‎．‎ ‎（1）求四棱锥P-ABCD的体积；‎ ‎（2）若E是PB的中点，求异面直线DE与PA所成角的大小（结果用反三角函数值表示）．‎ ‎ 6 / 6‎ ‎20. 在平面直角坐标系xOy中，直线l与抛物线y‎2‎‎=2x相交于A，B两点．‎ ‎(1)‎求证：“如果直线l过点T(3, 0)‎，那么OA‎→‎‎⋅OB‎→‎=3‎”是真命题；‎ ‎(2)‎写出‎(1)‎中命题的逆命题，判断它是真命题还是假命题，并说明理由．‎ ‎21. 已知有穷数列‎{an}‎共有‎2k项（整数k≥2‎），首项a‎1‎‎=2‎．设该数列的前n项和为Sn，且an+1‎‎=(a-1)Sn+2(n=1, 2‎,…,‎2k-1)‎，其中常数a>1‎．‎ ‎（1）求证：数列‎{an}‎是等比数列；‎ ‎（2）若a=‎‎2‎‎2‎‎2k-1‎，数列‎{bn}‎满足bn‎=‎1‎nlog‎2‎(a‎1‎a‎2‎…an)(n=1, 2‎,…,‎2k)‎，求数列‎{bn}‎的通项公式；‎ ‎（3）若（2）中的数列‎{bn}‎满足不等式‎|b‎1‎-‎3‎‎2‎|+|b‎2‎-‎3‎‎2‎|+...+|b‎2k-1‎-‎3‎‎2‎|+|b‎2k-‎3‎‎2‎|≤4‎，求k的值．‎ ‎22. 已知函数y=x+‎ax有如下性质：如果常数a>0‎，那么该函数在‎(0, a]‎上是减函数，在‎[a, +∞)‎上是增函数．‎ ‎(I)‎如果函数y=x+‎2‎bx(x>0)‎的值域为‎[6, +∞)‎，求b的值；‎ ‎(II)‎研究函数y=x‎2‎+‎cx‎2‎（常数c>0‎）在定义域内的单调性，并说明理由；‎ ‎(III)‎对函数y=x+‎ax和y=x‎2‎+‎ax‎2‎（常数a>0‎）作出推广，使它们都是你所推广的函数的特例．研究推广后的函数的单调性（只须写出结论，不必证明），并求函数F(x)=(x‎2‎+‎1‎x‎)‎n+(‎1‎x‎2‎+x‎)‎n（n是正整数）在区间‎[‎1‎‎2‎, 2]‎上的最大值和最小值（可利用你的研究结论）．‎ ‎ 6 / 6‎ 参考答案与试题解析 ‎2006年上海市高考数学试卷（理科）‎ 一、填空题（共12小题，每小题4分，满分48分）‎ ‎1.‎‎1‎ ‎2.‎‎2‎‎2‎ ‎3.‎‎1‎‎2‎ ‎4.‎‎1‎‎6‎ ‎5.‎i-1‎ ‎6.‎‎2‎‎6‎‎5‎ ‎7.‎x‎2‎‎16‎‎+y‎2‎‎4‎=1‎ ‎8.‎‎5‎ ‎9.‎‎1‎‎35‎ ‎10.‎‎36‎ ‎11.k=0‎，‎b∈(-1, 1)‎ ‎12.‎‎(-∞, 10]‎ 二、选择题（共4小题，每小题4分，满分16分）‎ ‎13.C ‎14.A ‎15.A ‎16.D 三、解答题（共6小题，满分86分）‎ ‎17.解：‎y=2cos(x+π‎4‎)cos(x-π‎4‎)+‎3‎sin2x ‎=2(‎1‎‎2‎cos‎2‎x-‎1‎‎2‎sin‎2‎x)+‎3‎sin2x ‎=cos2x+‎3‎sin2x ‎=2sin(2x+π‎6‎)‎ ‎∴ 函数y=2cos(x+π‎4‎)cos(x-π‎4‎)+‎3‎sin2x的值域是‎[-2, 2]‎，‎ 最小正周期是π；‎ ‎18.解：连接BC，‎ 由余弦定理得 BC‎2‎=‎20‎‎2‎+‎10‎‎2‎-2×20×10COS‎120‎‎∘‎=700‎‎．‎ 于是，‎BC=10‎‎7‎ ‎∵ sinACB‎20‎‎=‎sin‎120‎‎∘‎‎10‎‎7‎，‎ ‎∴ sin∠ACB=‎‎3‎‎7‎，‎ ‎∵ ‎‎∠ACB<‎‎90‎‎∘‎ ‎∴ ‎‎∠ACB=‎‎41‎‎∘‎ ‎∴ 乙船应朝北偏东‎71‎‎∘‎方向沿直线前往B处救援．‎ ‎19.解：（1）在四棱锥P-ABCD中，由PO⊥‎平面ABCD，得 ‎∠PBO是PB与平面ABCD所成的角，‎∠PBO=‎‎60‎‎∘‎．‎ 在Rt△AOB中BO=ABsin‎30‎‎∘‎=1‎，由PO⊥BO，‎ 于是，PO=BOtan‎60‎‎∘‎=‎‎3‎，而底面菱形的面积为‎2‎‎3‎．‎ ‎∴ 四棱锥P-ABCD的体积V=‎1‎‎3‎×2‎3‎×‎3‎=2‎．‎ ‎（2）解法一：以O为坐标原点，射线OB、OC、‎ OP分别为x轴、y轴、z轴的正半轴建立空间直角坐标系．‎ ‎ 6 / 6‎ 在Rt△AOB中OA=‎‎3‎，于是，点A、B、‎ D‎、P的坐标分别是A(0, -‎3‎, 0)‎，‎ B(1, 0, 0)‎‎，D(-1, 0, 0)‎，P(0, 0, ‎3‎)‎．‎ E是PB的中点，则E(‎1‎‎2‎, 0, ‎3‎‎2‎)‎于是DE‎→‎‎=(‎3‎‎2‎, 0, ‎3‎‎2‎)‎，AP‎→‎‎=(0, ‎3‎, ‎3‎)‎．‎ 设DE‎→‎与AP‎→‎的夹角为θ，有cosθ=‎3‎‎2‎‎⋅‎=‎‎2‎‎4‎，θ=arccos‎2‎‎4‎，‎ ‎∴ 异面直线DE与PA所成角的大小是arccos‎2‎‎4‎；‎ 解法二：取AB的中点F，连接EF、DF．‎ 由E是PB的中点，得EF // PA，‎ ‎∴ ‎∠FED是异面直线DE与PA所成 角（或它的补角），‎ 在Rt△AOB中AO=ABcos‎30‎‎∘‎=‎3‎=OP，‎ 于是，在等腰Rt△POA中，‎ PA=‎‎6‎‎，则EF=‎‎6‎‎2‎．‎ 在正‎△ABD和正‎△PBD中，DE=DF=‎‎3‎，‎ cos∠FED=‎1‎‎2‎EFDE=‎6‎‎4‎‎3‎=‎‎2‎‎4‎ ‎∴ 异面直线DE与PA所成角的大小是arccos‎2‎‎4‎．‎ ‎20.‎(1)‎证明：设过点T(3, 0)‎的直线l交抛物线y‎2‎‎=2x于点A(x‎1‎, y‎1‎)‎、B(x‎2‎, y‎2‎)‎．‎ 当直线l的斜率不存在时，直线l的方程为x=3‎，‎ 此时，直线l与抛物线相交于点A(3, ‎6‎)‎、B(3, -‎6‎)‎．‎ ‎∴ OA‎→‎‎⋅OB‎→‎=3‎；‎ 当直线l的斜率存在时，设直线l的方程为y=k(x-3)‎，其中k≠0‎，‎ 由y‎2‎‎=2xy=k(x-3)‎得ky‎2‎-2y-6k=0⇒y‎1‎y‎2‎=-6‎ 又∵ x‎1‎‎=‎1‎‎2‎y‎1‎‎2‎，x‎2‎=‎‎1‎‎2‎y‎2‎‎2‎，‎ ‎∴ OA‎→‎‎⋅OB‎→‎=x‎1‎x‎2‎+y‎1‎y‎2‎=‎1‎‎4‎(y‎1‎y‎2‎‎)‎‎2‎+y‎1‎y‎2‎=3‎，‎ 综上所述，命题“如果直线l过点T(3, 0)‎，那么OA‎→‎‎⋅OB‎→‎=3‎”是真命题.‎ ‎(2)‎解：逆命题是：设直线l交抛物线y‎2‎‎=2x于A、B两点，‎ 如果OA‎→‎‎⋅OB‎→‎=3‎，那么该直线过点T(3, 0)‎．该命题是假命题．‎ 例如：取抛物线上的点A(2, 2)‎，B(‎1‎‎2‎, 1)‎，‎ 此时OA‎→‎‎⋅OB‎→‎=3‎，‎ 直线AB的方程为：y=‎2‎‎3‎(x+1)‎，而T(3, 0)‎不在直线AB上；‎ 说明：由抛物线y‎2‎‎=2x上的点A(x‎1‎, y‎1‎)‎、B(x‎2‎, y‎2‎)‎满足OA‎→‎‎⋅OB‎→‎=3‎，可得y‎1‎y‎2‎‎=-6‎，‎ 或y‎1‎y‎2‎‎=2‎，如果y‎1‎y‎2‎‎=-6‎，可证得直线AB过点‎(3, 0)‎；如果y‎1‎y‎2‎‎=2‎，可证得直线 AB过点‎(-1, 0)‎，而不过点‎(3, 0)‎．‎ ‎21.解：由题意：（1）证明：‎ ‎ 6 / 6‎ 当n=1‎时，a‎2‎‎=2a，则a‎2‎a‎1‎‎=a；‎ 当‎2≤n≤2k-1‎时，an+1‎‎=(a-1)Sn+2‎，an‎=(a-1)Sn-1‎+2‎，‎ ‎∴ an+1‎‎-an=(a-1)‎an，‎ ‎∴ an+1‎an‎=a，‎ ‎∴ 数列‎{an}‎是等比数列．‎ ‎（2）解：由（1）得an‎=2‎an-1‎，‎ ‎∴ a‎1‎a‎2‎an‎=‎2‎na‎1+2+…+（n-1）‎=‎2‎nan(n-1)‎‎2‎=‎‎2‎n+‎n(n-1)‎‎2k-1‎，‎ bn‎=‎1‎n[n+n(n-1)‎‎2k-1‎]=n-1‎‎2k-1‎+1(n=1, 2, 2k)‎‎．‎ ‎（3）设bn‎≤‎‎3‎‎2‎，解得n≤k+‎‎1‎‎2‎，又n是正整数，于是当n≤k时，bn‎<‎‎3‎‎2‎；‎ 当n≥k+1‎时，bn‎>‎‎3‎‎2‎．‎ 原式‎=(‎3‎‎2‎-b‎1‎)+(‎3‎‎2‎-b‎2‎)+...+(‎3‎‎2‎-bk)+(bk+1‎-‎3‎‎2‎)+...+(b‎2k-‎3‎‎2‎)‎ ‎=(bk+1‎+...+b‎2k)-(b‎1‎+...+bk)‎ ‎=[‎1‎‎2‎‎(k+2k-1)k‎2k-1‎+k]-[‎1‎‎2‎‎(0+k-1)k‎2k-1‎+k]=‎k‎2‎‎2k-1‎‎．‎ 当k‎2‎‎2k-1‎‎≤4‎，得k‎2‎‎-8k+4≤0‎，‎4-2‎3‎≤k≤4+2‎‎3‎，又k≥2‎，‎ ‎∴ 当k=2‎，‎3‎，‎4‎，‎5‎，‎6‎，‎7‎时，‎ 原不等式成立．‎ ‎22.解：‎(1)‎函数y=x+‎2‎bx(x>0)‎的最小值是‎2‎‎2‎b，则‎2‎2‎b=6‎，‎ ‎∴ b=log‎2‎9‎．‎ ‎(2)‎设‎0‎y‎1‎，函数y=x‎2‎+‎cx‎2‎在‎[‎‎4‎c，‎+∞)‎上是增函数；‎ 当‎00‎），其中n是正整数．‎ 当n是奇数时，函数y=xn+‎axn在‎(0, ‎2na]‎上是减函数，在‎[‎‎2na，‎+∞)‎上是增函数，‎ 在‎(-∞, -‎2na]‎上是增函数，在‎[-‎‎2na，‎0)‎上是减函数；‎ 当n是偶数时，函数y=xn+‎axn在‎(0, ‎2na]‎上是减函数，在‎[‎‎2na，‎+∞)‎上是增函数，‎ 在‎(-∞, -‎2na]‎上是减函数，在‎[-‎‎2na，‎0)‎上是增函数；‎ F(x)=(x‎2‎+‎1‎x‎)‎n+(‎1‎x‎2‎+x‎)‎n ‎=Cn‎0‎(x‎2n+‎1‎x‎2n)+Cn‎1‎(x‎2n-2‎+‎1‎x‎2n-3‎)+...+Cnr(x‎2n-3r+‎1‎x‎2n-3r)+…+Cnn(xn+‎1‎xn)‎‎，‎ 因此F(x)‎在‎[‎1‎‎2‎, 1]‎上是减函数，在‎[1, 2]‎上是增函数．‎ 所以，当x=‎‎1‎‎2‎或x=2‎时，F(x)‎取得最大值‎(‎9‎‎2‎‎)‎n+(‎‎9‎‎4‎‎)‎n；‎ 当x=1‎时F(x)‎取得最小值‎2‎n+1‎；‎ ‎ 6 / 6‎