2021届高考数学一轮复习第四章三角函数解三角形第2节同角三角函数的基本关系式与诱导公式课件新人教A版

2021届高考数学一轮复习第四章三角函数解三角形第2节同角三角函数的基本关系式与诱导公式课件新人教A版

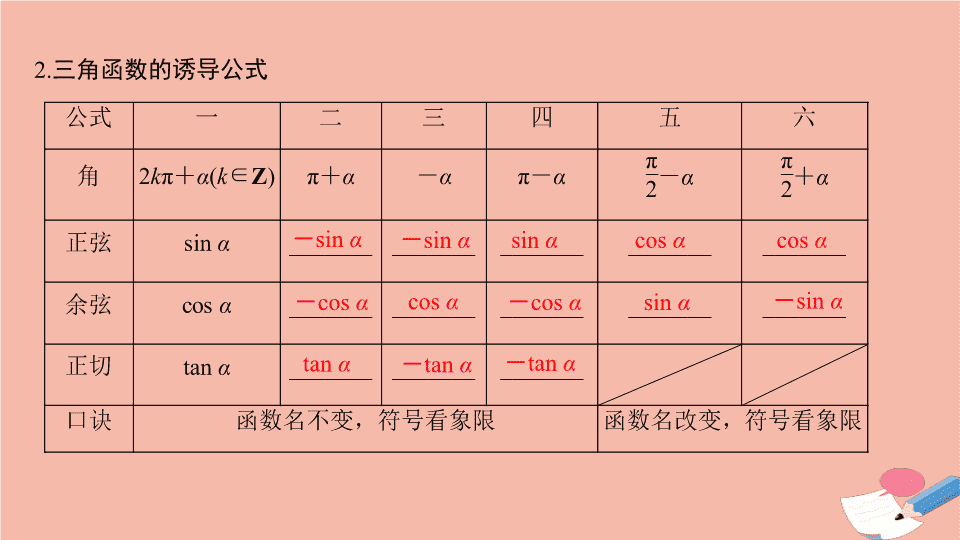
第 2 节　同角三角函数的基本关系式与诱导公式 知 识 梳 理 1. 同角三角函数的基本关系 (1) 平方关系： _________________. (2) 商数关系： _________________. sin 2 α ＋ cos 2 α ＝ 1 2. 三角函数的诱导公式 － sin α － sin α sin α cos α cos α － cos α cos α － cos α sin α － sin α tan α － tan α － tan α 诊 断 自 测 1. 判断下列结论正误 ( 在括号内打 “√” 或 “×” ) 解析　 (1) 对任意的角 α ， sin 2 α ＋ cos 2 α ＝ 1. (2) 中对于任意 α ∈ R ，恒有 sin(π ＋ α ) ＝－ sin α . (3) 中当 α 的终边落在 y 轴上，商数关系不成立 . 答案　 A 答案　 A 答案　 A 答案　 D 解析　 ∵ f (8) ＝ cos(4π ＋ α ) ＋ 1 ＝ cos α ＋ 1 ＝ 2 ， ＝ cos(1 009π ＋ α ) ＋ 1 ＝ cos(π ＋ α ) ＋ 1 ＝－ cos α ＋ 1 ＝－ 1 ＋ 1 ＝ 0. 答案　 0 考点一　同角三角函数基本关系及其应用 多维探究 角度 1 　切弦互化 角度 2 　 “1” 的变换 答案　 (1)D 　 (2)D 规律方法　 注意公式的逆用及变形应用： 1 ＝ sin 2 α ＋ cos 2 α ， sin 2 α ＝ 1 － cos 2 α ， cos 2 α ＝ 1 － sin 2 α . 角度 3 　 sin α ±cos α 与 sin α cos α 的转化 答案　 B 规律方法　 应用公式时注意方程思想的应用：对于 sin α ＋ cos α ， sin α cos α ， sin α － cos α 这三个式子，利用 (sin α ±cos α ) 2 ＝ 1±2sin α cos α ，可以知一求二 . 考点二　诱导公式的应用 规律方法　 (1) 诱导公式的两个应用 ① 求值：负化正，大化小，化到锐角为终了 . ② 化简：统一角，统一名，同角名少为终了 . (2) 含 2π 整数倍的诱导公式的应用 由终边相同的角的关系可知，在计算含有 2π 的整数倍的三角函数式中可直接将 2π 的整数倍去掉后再进行运算 . 如 cos(5π － α ) ＝ cos(π － α ) ＝－ cos α . 考点三　同角三角函数基本关系式和诱导公式的综合应用 规律方法　 1. 利用同角三角函数关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式进行变形 . 2. 注意角的范围对三角函数值符号的影响 . (2) ∵ sin α >0 ， ∴ α 为第一或第二象限角，