山东省泰安市2019-2020学年高一下学期期末考试数学试题（可编辑） PDF版含答案

山东省泰安市2019-2020学年高一下学期期末考试数学试题（可编辑） PDF版含答案

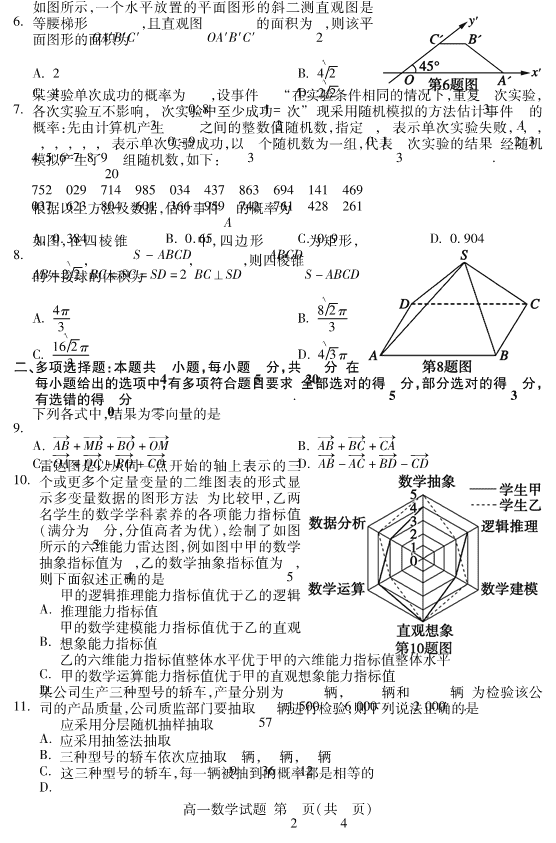
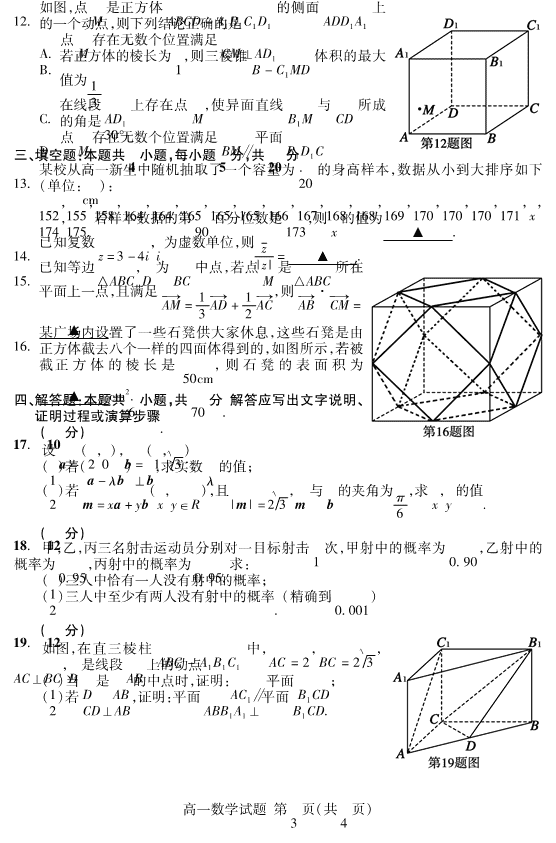
书书书 试卷类型：Ａ高一年级考试 数　 学　 试　 题 ２０２０ ７ 注意事项： １． 答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。 ２． 回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。 如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡 上。写在本试卷上无效。 ３． 考试结束后，将本试卷和答题卡一并交回。 一、单项选择题：本题共 ８ 小题，每小题 ５ 分，共 ４０ 分． 在每小题给出的四个选项中，只有 一项是符合题目要求的． １． 在复平面内，复数 ２ １ － ｉ对应的点位于 Ａ． 第一象限　 　 　 　 Ｂ． 第二象限　 　 　 　 Ｃ． 第三象限　 　 　 　 Ｄ． 第四象限 ２． 在一个随机试验中，彼此互斥的事件 Ａ，Ｂ，Ｃ，Ｄ 发生的概率分别为 ０． １，０． １，０． ４，０． ４， 则下列说法正确的是 Ａ． Ａ 与 Ｂ ＋ Ｃ 是互斥事件，也是对立事件 Ｂ． Ｂ ＋ Ｃ 与 Ｄ 是互斥事件，也是对立事件 Ｃ． Ａ ＋ Ｂ 与 Ｃ ＋ Ｄ 是互斥事件，但不是对立事件 Ｄ． Ａ ＋ Ｃ 与 Ｂ ＋ Ｄ 是互斥事件，也是对立事件 ３． 在△ＡＢＣ 中，ＡＢ ＝ ２，ＢＣ ＝ ３，ＡＣ 槡＝ １０ ，则 ｃｏｓＢ ＝ Ａ． 槡１０ ８ Ｂ． １ ４ Ｃ． 槡１０ ４ Ｄ． １ ２ ４． 如图，非零向量 →ＯＡ ＝ ａ，→ＯＢ ＝ ｂ，且 ＢＣ⊥ＯＡ，Ｃ 为垂足，设向量 →ＯＣ ＝ λａ，则 λ 的值为 Ａ． ａ·ｂ ｜ ａ ｜ ２ Ｂ． ａ·ｂ ｜ ａ ｜ ｜ ｂ ｜ Ｃ． ａ·ｂ ｜ ｂ ｜ ２ Ｄ． ｜ ａ ｜ ｜ ｂ ｜ ａ·ｂ ５． 某班统计一次数学测验的平均分与方差，计算完毕才发现有位同 学的分数还未录入，只好重算一次． 已知原平均分和原方差分别为 ｘ，ｓ２ ，新平均分和新 方差分别为 ｘ１ ，ｓ２ １ ，若此同学的得分恰好为 ｘ，则 Ａ． ｘ ＝ ｘ１ ，ｓ２ ＝ ｓ２ １ Ｂ． ｘ ＝ ｘ１ ，ｓ２ ＜ ｓ２ １ Ｃ． ｘ ＝ ｘ１ ，ｓ２ ＞ ｓ２ １ Ｄ． ｘ ＜ ｘ１ ，ｓ２ ＝ ｓ２ １ 高一数学试题 第 １ 页（共 ４ 页） ６． 如图所示，一个水平放置的平面图形的斜二测直观图是等腰梯形 ＯＡ′Ｂ′Ｃ′，且直观图 ＯＡ′Ｂ′Ｃ′的面积为 ２，则该平面图形的面积为 Ａ． ２ Ｂ． 槡４ ２ Ｃ． 槡４ Ｄ． ２ ２ ７． 某实验单次成功的概率为 ０． ８，设事件 Ａ ＝ “在实验条件相同的情况下，重复 ３ 次实验，各次实验互不影响，３ 次实验中至少成功 ２ 次”． 现采用随机模拟的方法估计事件 Ａ 的概率：先由计算机产生 ０ ～ ９ 之间的整数值随机数，指定 ０，１ 表示单次实验失败，２，３， ４，５，６，７，８，９ 表示单次实验成功，以 ３ 个随机数为一组，代表 ３ 次实验的结果． 经随机模拟产生了 ２０ 组随机数，如下： ７５２　 ０２９　 ７１４　 ９８５　 ０３４　 ４３７　 ８６３　 ６９４　 １４１　 ４６９ ０３７　 ６２３　 ８０４　 ６０１　 ３６６　 ９５９　 ７４２　 ７６１　 ４２８　 ２６１根据以上方法及数据，估计事件 Ａ 的概率为 Ａ． ０． ３８４ Ｂ． ０． ６５ Ｃ． ０． ９ Ｄ． ０． ９０４ ８． 如图，在四棱锥 Ｓ － ＡＢＣＤ 中，四边形 ＡＢＣＤ 为矩形， ＡＢ 槡＝ ２ ２ ，ＢＣ ＝ ＳＣ ＝ ＳＤ ＝ ２，ＢＣ⊥ＳＤ，则四棱锥Ｓ － ＡＢＣＤ的外接球的体积为 Ａ． ４π ３ Ｂ． 槡８ ２ π ３ Ｃ． 槡１６ ２ π ３ 槡Ｄ． ４ ３ π 二、多项选择题：本题共 ４ 小题，每小题 ５ 分，共 ２０ 分． 在每小题给出的选项中，有多项符合题目要求． 全部选对的得 ５ 分，部分选对的得 ３ 分，有选错的得 ０ 分． ９． 下列各式中，结果为零向量的是 Ａ． →ＡＢ ＋ →ＭＢ ＋ →ＢＯ ＋ →ＯＭ Ｂ． →ＡＢ ＋ →ＢＣ ＋ →ＣＡ Ｃ． →ＯＡ ＋ →ＯＣ ＋ →ＢＯ ＋ →ＣＯ Ｄ． →ＡＢ － →ＡＣ ＋ →ＢＤ － →ＣＤ １０． 雷达图是以从同一点开始的轴上表示的三个或更多个定量变量的二维图表的形式显示多变量数据的图形方法． 为比较甲，乙两名学生的数学学科素养的各项能力指标值（满分为 ５ 分，分值高者为优），绘制了如图所示的六维能力雷达图，例如图中甲的数学抽象指标值为 ４，乙的数学抽象指标值为 ５，则下面叙述正确的是 Ａ． 甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值 Ｂ． 甲的数学建模能力指标值优于乙的直观想象能力指标值 Ｃ． 乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平 Ｄ． 甲的数学运算能力指标值优于甲的直观想象能力指标值 １１． 某公司生产三种型号的轿车，产量分别为 １ ５００ 辆，６ ０００ 辆和 ２ ０００ 辆． 为检验该公司的产品质量，公司质监部门要抽取 ５７ 辆进行检验，则下列说法正确的是 Ａ． 应采用分层随机抽样抽取 Ｂ． 应采用抽签法抽取 Ｃ． 三种型号的轿车依次应抽取 ９ 辆，３６ 辆，１２ 辆 Ｄ． 这三种型号的轿车，每一辆被抽到的概率都是相等的 高一数学试题 第 ２ 页（共 ４ 页） １２． 如图，点 Ｍ 是正方体 ＡＢＣＤ － Ａ１ Ｂ１ Ｃ１ Ｄ１ 的侧面 ＡＤＤ１ Ａ１ 上的一个动点，则下列结论正确的是 Ａ． 点 Ｍ 存在无数个位置满足 ＣＭ⊥ＡＤ１ Ｂ． 若正方体的棱长为 １，则三棱锥 Ｂ － Ｃ１ ＭＤ 体积的最大 值为 １ ３ Ｃ． 在线段 ＡＤ１ 上存在点 Ｍ，使异面直线 Ｂ１ Ｍ 与 ＣＤ 所成的角是 ３０° Ｄ． 点 Ｍ 存在无数个位置满足 ＢＭ∥平面 Ｂ１ Ｄ１ Ｃ三、填空题：本题共 ４ 小题，每小题 ５ 分，共 ２０ 分． １３． 某校从高一新生中随机抽取了一个容量为 ２０ 的身高样本，数据从小到大排序如下（单位：ｃｍ）： １５２，１５５，１５８，１６４，１６４，１６５，１６５，１６５，１６６，１６７，１６８，１６８，１６９，１７０，１７０，１７０，１７１，ｘ， １７４，１７５． 若样本数据的第 ９０ 百分位数是 １７３，则 ｘ 的值为　 　 ▲　 　 ． １４． 已知复数 ｚ ＝ ３ － ４ｉ，ｉ 为虚数单位，则 ｚ ｜ ｚ｜ ＝ 　 　 ▲　 　 ． １５． 已知等边△ＡＢＣ，Ｄ 为 ＢＣ 中点，若点 Ｍ 是△ＡＢＣ 所在 平面上一点，且满足 →ＡＭ ＝ １ ３ →ＡＤ ＋ １ ２ →ＡＣ，则 →ＡＢ· →ＣＭ ＝ 　 　 ▲　 　 ． １６． 某广场内设置了一些石凳供大家休息，这些石凳是由正方体截去八个一样的四面体得到的，如图所示，若被截正方体的棱长是 ５０ｃｍ，则石凳的表面积为 　 　 ▲　 　 ｃｍ２ ．四、解答题：本题共 ６ 小题，共 ７０ 分． 解答应写出文字说明、证明过程或演算步骤． １７． （１０ 分）设 ａ ＝ （２，０），ｂ ＝ （１，槡３ ）．（１）若（ａ － λｂ）⊥ｂ，求实数 λ 的值； （２）若 ｍ ＝ ｘａ ＋ ｙｂ（ｘ，ｙ∈Ｒ），且｜ ｍ 槡｜ ＝ ２ ３ ，ｍ 与 ｂ 的夹角为 π ６ ，求 ｘ，ｙ 的值． １８． （１２ 分）甲，乙，丙三名射击运动员分别对一目标射击 １ 次，甲射中的概率为 ０． ９０，乙射中的概率为 ０． ９５，丙射中的概率为 ０． ９５． 求：（１）三人中恰有一人没有射中的概率；（２）三人中至少有两人没有射中的概率． （精确到 ０． ００１） １９． （１２ 分）如图，在直三棱柱 ＡＢＣ － Ａ１ Ｂ１ Ｃ１ 中，ＡＣ ＝ ２，ＢＣ 槡＝ ２ ３ ， ＡＣ⊥ＢＣ，Ｄ 是线段 ＡＢ 上的动点．（１）当 Ｄ 是 ＡＢ 的中点时，证明：ＡＣ１ ∥平面 Ｂ１ ＣＤ；（２）若 ＣＤ⊥ＡＢ，证明：平面 ＡＢＢ１ Ａ１ ⊥平面 Ｂ１ ＣＤ． 高一数学试题 第 ３ 页（共 ４ 页） ２０． （１２ 分）请从下面三个条件中任选一个，补充在下面的横线上，并作答． ①ｓｉｎＡ － ｓｉｎＣ ｂ ＝ ｓｉｎＡ － ｓｉｎＢ ａ ＋ ｃ ； ②２ｃｃｏｓＣ ＝ ａｃｏｓＢ ＋ ｂｃｏｓＡ； ③△ＡＢＣ 的面积为 １ ２ ｃ（ａｓｉｎＡ ＋ ｂｓｉｎＢ － ｃｓｉｎＣ）． 已知△ＡＢＣ 的内角 Ａ，Ｂ，Ｃ 的对边分别为 ａ，ｂ，ｃ，且 ．（１）求 Ｃ；（２）若 Ｄ 为 ＡＢ 中点，且 ｃ ＝ ２，ＣＤ 槡＝ ３ ，求 ａ，ｂ．注：如果选择多个条件分别解答，按第一个解答计分． ２１． （１２ 分）“肥桃”因产于山东省泰安市肥城市境内而得名，已有 １１００ 多年的栽培历史． 明代万历十一年（１５８３ 年）的《肥城县志》载：“果亦多品，惟桃最著名”． ２０１６ 年 ３ 月 ３１ 日，原中华人民共和国农业部批准对“肥桃”实施国家农产品地理标志登记保护． 某超市在旅游旺季销售一款肥桃，进价为每个 １０ 元，售价为每个 １５ 元． 销售的方案是当天进货，当天销售，未售出的全部由厂家以每个 ５ 元的价格回购处理． 根据该超市以往的销售情况，得到如图所示的频率分布直方图： （１）估算该超市肥桃日需求量的平均数 （同一组中的数据用该组区间的中点值代表）；（２）已知该超市某天购进了 １５０ 个肥桃，假设当天的需求量为 ｘ 个（ｘ ∈ Ｎ， ０≤ｘ≤２４０），销售利润为 ｙ 元．（ｉ）求 ｙ 关于 ｘ 的函数关系式；（ｉｉ）结合上述频率分布直方图，以频率估计概率的思想，估计当天利润 ｙ 不小于 ６５０元的概率． ２２． （１２ 分）《九章算术》是中国古代的一部数学专著，是《算经十书》中最重要的一部，成于公元一世纪左右． 它是一本综合性的历史著作，是当时世界上最简练有效的应用数学，它的出现标志着中国古代数学形成了完整的体系． 《九章算术》中将由四个直角三角形组成的四面体称为“鳖”． 已知在三棱锥 Ｐ － ＡＢＣ 中，ＰＡ⊥平面 ＡＢＣ．（１ ）从 三 棱 锥 Ｐ － ＡＢＣ 中 选 择 合 适 的 两 条 棱 填 空： ⊥ ，则三棱锥 Ｐ － ＡＢＣ 为“鳖”；（２ ）如图，已知 ＡＤ ⊥ ＰＢ，垂足为 Ｄ，ＡＥ ⊥ ＰＣ，垂足为 Ｅ， ∠ＡＢＣ ＝ ９０°．（ⅰ）证明：平面 ＡＤＥ⊥平面 ＰＡＣ；（ⅱ）设平面 ＡＤＥ 与平面 ＡＢＣ 的交线为 ｌ，若 ＰＡ 槡＝ ２ ３ ，ＡＣ ＝ ２，求二面角 Ｅ － ｌ － Ｃ 的大小． 高一数学试题 第 ４ 页（共 ４ 页） 高一年级考试 数学参考答案及评分标准 ２０２０ ７ 一、单项选择题： 题　 号 １ ２ ３ ４ ５ ６ ７ ８ 答　 案 Ａ Ｄ Ｂ Ａ Ｃ Ｂ Ｃ Ｄ 二、多项选择题： 题　 号 ９ １０ １１ １２ 答　 案 ＢＤ ＡＣ ＡＣＤ ＡＢＤ 三、填空题： １３． １７２　 　 　 １４． ３ ５ ＋ ４ ５ ｉ　 　 　 １５． ０　 　 　 １６． 槡７５００ ＋ ２５００ ３ 四、解答题： １７． （１０ 分）解：（１）∵ ａ ＝ （２，０），ｂ ＝ （１，槡３ ）， ∴ ａ － λｂ ＝ （２ － λ， 槡－ ３ λ）， ２ 分!!!!!!!!!!!!!!!!!! ∵ （ａ － λｂ）⊥ｂ， ∴ （ａ － λｂ）·ｂ ＝ ０，即 ２ － ４λ ＝ ０， ∴ λ ＝ １ ２ ． ４ 分!!!!!!!!!!!!!!!!!!!!!!!!!! （２）∵ ａ ＝ （２，０），ｂ ＝ （１，槡３ ）， ∴ ｍ ＝ ｘａ ＋ ｙｂ ＝ （２ｘ ＋ ｙ，槡３ ｙ），又｜ ｍ 槡｜ ＝ ２ ３ ， ∴ （２ｘ ＋ ｙ）２ ＋ ３ｙ２ ＝ １２， ６ 分!!!!!!!!!!!!!!!!!!!! 又 ｃｏｓ π ６ ＝ ｍ·ｂ ｜ ｍ｜ ｜ ｂ ｜ ＝ ２ｘ ＋ ｙ ＋ ３ｙ 槡２ ３ × ２ ＝ 槡３ ２ ， 即 ｘ ＋ ２ｙ ＝ ３， ８ 分!!!!!!!!!!!!!!!!!!!!!!!! 由 （２ｘ ＋ ｙ）２ ＋ ３ｙ２ ＝ １２ ｘ ＋ ２ｙ{ ＝ ３ ， 解得 ｘ ＝ １ ｙ{ ＝ １或 ｘ ＝ － １ ｙ{ ＝ ２ ， ∴ ｘ ＝ １，ｙ ＝ １ 或 ｘ ＝ － １，ｙ ＝ ２． １０ 分!!!!!!!!!!!!!!!!! １８． （１２ 分）解：设甲，乙，丙三人射击 １ 次射中目标的事件为 Ａ，Ｂ，Ｃ．（１）Ｐ（Ａ）＝ ０． ９０，Ｐ（Ｂ）＝ Ｐ（Ｃ）＝ ０． ９５，Ｐ（ ）＝ ０． １０，Ｐ（ ） ＝ Ｐ（ ）＝ ０． ０５， ３ 分!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! ∵ 事件 Ａ，Ｂ，Ｃ 相互独立， ∴ 三人中恰有一人没有射中的概率为 Ｐ（ＡＢ ）＋ Ｐ（Ａ Ｃ）＋ Ｐ（ ＢＣ） ＝ Ｐ（Ａ）Ｐ（Ｂ）Ｐ（ ）＋ Ｐ（Ａ）Ｐ（ ）Ｐ（Ｃ）＋ Ｐ（ ）Ｐ（Ｂ）Ｐ（Ｃ） ＝ ２ × ０． ９０ × ０． ９５ × ０． ０５ ＋ ０． １０ × ０． ９５ × ０． ９５≈０． １７６ 高一数学试题参考答案 第 １ 页（共 ４ 页） ∴ 三人中恰有一人没有射中的概率为 ０． １７６． ６ 分!!!!!!!!!!!（２）解法一：三人中至少有两人没有射中的概率为 Ｐ（Ａ ）＋ Ｐ（ Ｂ ）＋ Ｐ（ Ｃ）＋ Ｐ（ ） ＝ ０ ９０ × ０ ０５２ ＋ ２ × ０ １０ × ０ ０５ × ０ ９５ ＋ ０ １０ × ０ ０５２ ＝ ０ ０１２ ９ 分!!!!!!!!!!!!!!!!!!!!!!!!!! ∴ 三人中至少有两人没有射中的概率为 ０． ０１２． １２ 分!!!!!!!!!解法二：三人都射中的概率为 Ｐ（ＡＢＣ）＝ Ｐ（Ａ）Ｐ（Ｂ）Ｐ（Ｃ） ＝ ０． ９０ × ０． ９５２ ≈０． ８１２ ９ 分!!!!!!!!!!!!!!!!!!!!!!!由（１）知，三人中恰有一人没有射中的概率为 ０． １７６， ∴ 三人中至少有两人没有射中的概率为 １ － Ｐ（ＡＢＣ）－ ０． １７６ ＝ １ － （０． ８１２ ＋ ０． １７６） ＝ ０． ０１２ ∴ 三人中至少有两人没有射中的概率为 ０． ０１２． １２ 分!!!!!!!!! １９． （１２ 分）解：（１）证明：如图，连接 ＢＣ１ ，交 Ｂ１ Ｃ 于 Ｅ，连接 ＤＥ，则 Ｅ 是 ＢＣ１ 的中点， ∵ Ｄ 是 ＡＢ 的中点， ∴ ＤＥ∥ＡＣ１ ， ３ 分!!!!!!!!!!!!!!!!!!!!!!!!!又 ＤＥ 平面 Ｂ１ ＣＤ，ＡＣ１ 平面 Ｂ１ ＣＤ， ∴ ＡＣ１ ∥平面 Ｂ１ ＣＤ ． ６ 分!!!!!!!!!!!!!!!!!!!!!（２）证明：∵ ＡＡ１ ⊥平面 ＡＢＣ，ＣＤ 平面 ＡＢＣ， ∴ ＡＡ１ ⊥ＣＤ， ８ 分!!!!!!!!!!!!!!又 ＣＤ⊥ＡＢ，ＡＡ１ ∩ＡＢ ＝ Ａ，ＡＢ，ＡＡ１ 平面 ＡＢＢ１ Ａ１ ， ∴ ＣＤ⊥平面 ＡＢＢ１ Ａ１ ， １０ 分!!!!!!!!!!又 ＣＤ 平面 Ｂ１ ＣＤ， ∴ 平面 ＡＢＢ１ Ａ１ ⊥平面 Ｂ１ ＣＤ． １２ 分!!!!!! ２０． （１２ 分）解：方案一：选条件① （１）∵ ｓｉｎＡ － ｓｉｎＣ ｂ ＝ ｓｉｎＡ － ｓｉｎＢ ａ ＋ ｃ ， ∴ ａ － ｃ ｂ ＝ ａ － ｂ ａ ＋ ｃ，即 ａ２ － ｃ２ ＝ ａｂ － ｂ２ ， ∴ ａ２ ＋ ｂ２ － ｃ２ ＝ ａｂ， ２ 分!!!!!!!!!!!!!!!!!!!!!! ∴ ｃｏｓＣ ＝ ａ２ ＋ ｂ２ － ｃ２ ２ａｂ ＝ １ ２ ． ∴ Ｃ ＝ π ３ ． ４ 分!!!!!!!!!!!!!!!!!!!!!!!!!! （２）由题意知，ＡＤ ＝ ＢＤ ＝ １，ＣＤ 槡＝ ３ ，在△ＡＣＤ 中，ＡＣ２ ＝ ＡＤ２ ＋ ＣＤ２ － ２ＡＤ·ＣＤ·ｃｏｓ∠ＡＤＣ，即 ｂ２ 槡＝ ４ － ２ ３ ｃｏｓ∠ＡＤＣ． ６ 分!!!!!!!!!!!!!!!!!!!!在△ＢＣＤ 中，ＢＣ２ ＝ ＢＤ２ ＋ ＣＤ２ － ２ＢＤ·ＣＤ·ｃｏｓ∠ＢＤＣ，即 ａ２ 槡＝ ４ － ２ ３ ｃｏｓ∠ＢＤＣ， ８ 分!!!!!!!!!!!!!!!!!!! ∵ ∠ＡＤＣ ＋ ∠ＢＤＣ ＝ π， ∴ ｃｏｓ∠ＡＤＣ ＝ － ｃｏｓ∠ＢＤＣ， ∴ ａ２ ＋ ｂ２ ＝ ８． １０ 分!!!!!!!!!!!!!!!!!!!!!!!! 由（１）知，ｃｏｓＣ ＝ ａ２ ＋ ｂ２ － ｃ２ ２ａｂ ＝ １ ２ 高一数学试题参考答案 第 ２ 页（共 ４ 页） ∴ ａ２ ＋ ｂ２ ＝ ｃ２ ＋ ａｂ ＝ ４ ＋ ａｂ， ∴ ａｂ ＝ ４， 由 ａ２ ＋ ｂ２ ＝ ８ ａｂ{ ＝ ４ ，解得 ａ ＝ ｂ ＝ ２． １２ 分!!!!!!!!!!!!!!!!! 方案二：选条件②（１）∵ ２ｃｃｏｓＣ ＝ ａｃｏｓＢ ＋ ｂｃｏｓＡ， ∴ ２ｓｉｎＣｃｏｓＣ ＝ ｓｉｎＡｃｏｓＢ ＋ ｓｉｎＢｃｏｓＡ， ∴ ２ｓｉｎＣｃｏｓＣ ＝ ｓｉｎ（Ａ ＋ Ｂ）， ２ 分!!!!!!!!!!!!!!!!!!! ∴ ２ｓｉｎＣｃｏｓＣ ＝ ｓｉｎＣ． ∴ ｃｏｓＣ ＝ １ ２ ， ∴ Ｃ ＝ π ３ ． ４ 分!!!!!!!!!!!!!!!!!!!!!!!!!! （２）同方案一（２）方案三：选条件③ （１）由题意知，１ ２ ａｂｓｉｎＣ ＝ １ ２ ｃ（ａｓｉｎＡ ＋ ｂｓｉｎＢ － ｃｓｉｎＣ） ∴ ａｂｃ ＝ ｃ（ａ２ ＋ ｂ２ － ｃ２ ）， ∴ ａ２ ＋ ｂ２ － ｃ２ ＝ ａｂ， ２ 分!!!!!!!!!!!!!!!!!!!!!! ∴ ｃｏｓＣ ＝ ａ２ ＋ ｂ２ － ｃ２ ２ａｂ ＝ １ ２ ， ∴ Ｃ ＝ π ３ ． ４ 分!!!!!!!!!!!!!!!!!!!!!!!!!! （２）同方案一（２） ２１． （１２ 分）解：（１）设日需求量为 ｔ，则 ｔ∈［０，４０）的频率为 ０． ００１２５ × ４０ ＝ ０． ０５； ｔ∈［８０，１２０）的频率为 ０． ００７５ × ４０ ＝ ０． ３； ｔ∈［１２０，１６０）的频率为 ０． ００６２５ × ４０ ＝ ０． ２５； ｔ∈［２００，２４０］的频率为 ０． ００２５ × ４０ ＝ ０． １． ２ 分!!!!!!!!!!!! ∴ ｔ∈［４０，８０）与 ｔ∈［１６０，２００）的频率为１ － （０．０５ ＋０．３ ＋０．２５ ＋０．１） ２ ＝０．１５． ∴ 该超市肥城桃日需求量的平均数为 ｔ ＝ ０． ０５ × ２０ ＋ ０． １５ × ６０ ＋ ０． ３ × １００ ＋ ０． ２５ × １４０ ＋ ０． １５ × １８０ ＋ ０． １ × ２２０ ＝ １２４． ４ 分!!!!!!!!!!!!!!!!!!!!!!!!!!!（２）（ｉ）当 ｘ∈［１５０，２４０］时，ｙ ＝ １５０ × （１５ － １０）＝ ７５０； ６ 分!!!!!!!!!当 ｘ∈［０，１５０）时，ｙ ＝ （１５ － １０）ｘ － （１５０ － ｘ）（１０ － ５）＝ １０ｘ － ７５０， ∴ ｙ ＝ ７５０，１５０≤ｘ≤２４０ １０ｘ － ７５０，０≤ｘ{ ＜ １５０（ｘ∈Ｎ）． ８ 分!!!!!!!!!!!!!! （ｉｉ）由（ｉ）可知，ｙ ＝ ７５０，１５０≤ｘ≤２４０ １０ｘ － ７５０，０≤ｘ≤{ １５０（ｘ∈Ｎ）， 令 ｙ≥６５０，解得 １４０≤ｘ≤２４０， １０ 分!!!!!!!!!!!!!!!!!由频率分布直方图可知，日需求量 ｘ∈［１４０，２４０］的频率约为 ０ ２５ ２ ＋ ０ １５ ＋ ０ １ ＝ ０ ３７５， 以频率估计概率的思想，估计当天利润 ｙ 不小于 ６５０ 元的概率约为 ０． ３７５． １２ 分!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 高一数学试题参考答案 第 ３ 页（共 ４ 页） ２２． （１２ 分）解：（１）（１）ＢＣ⊥ＡＢ 或 ＢＣ⊥ＡＣ 或 ＢＣ⊥ＰＢ 或 ＢＣ⊥ＰＣ． ２ 分!!!!!!!!!!（２）（ⅰ）证明： ∵ ＰＡ⊥平面 ＡＢＣ，ＢＣ 平面 ＡＢＣ， ∴ ＰＡ⊥ＢＣ，又 ＢＣ⊥ＡＢ，ＰＡ∩ＡＢ ＝ Ａ，ＰＡ，ＡＢ 平面 ＰＡＢ， ∴ ＢＣ⊥平面 ＰＡＢ，又 ＡＤ 平面 ＰＡＢ， ∴ ＢＣ⊥ＡＤ，又 ＡＤ⊥ＰＢ，ＰＢ∩ＢＣ ＝ Ｂ，ＰＢ，ＢＣ 平面 ＰＢＣ， ∴ ＡＤ⊥平面 ＰＢＣ， ４ 分!!!!!!!!!!!!!又 ＰＣ 平面 ＰＢＣ， ∴ ＰＣ⊥ＡＤ，又 ＡＥ⊥ＰＣ，ＡＥ∩ＡＤ ＝ Ａ，ＡＤ，ＡＥ 平面 ＡＤＥ， ∴ ＰＣ⊥平面 ＡＤＥ，又 ＰＣ 平面 ＰＡＣ， ∴ 平面 ＡＤＥ⊥平面 ＰＡＣ． ６ 分!!!!!!!!!!!!!!!!!!!!（ⅱ）由题意知，在平面 ＰＢＣ 中，直线 ＤＥ 与直线 ＢＣ 相交．如图所示，设 ＤＥ∩ＢＣ ＝ Ｆ，连结 ＡＦ，则 ＡＦ 即为 ｌ． ∵ ＰＣ⊥平面 ＡＥＤ，ｌ 平面 ＡＥＤ， ∴ ＰＣ⊥ｌ， ８ 分!!!!!!!!!!!!!!!!!!!!!!!!!! ∵ ＰＡ⊥平面 ＡＢＣ，ｌ 平面 ＡＢＣ， ∴ ＰＡ⊥ｌ，又 ＰＡ∩ＰＣ ＝ Ｐ，ＰＡ，ＰＣ 平面 ＰＡＣ， ∴ ｌ⊥平面 ＰＡＣ，又 ＡＥ，ＡＣ 平面 ＰＡＣ， ∴ ＡＥ⊥ｌ，ＡＣ⊥ｌ． ∴ ∠ＥＡＣ 即为二面角 Ｅ － ｌ － Ｃ 的一个平面角． １０ 分!!!!!!!!!!!!!!!!在△ＰＡＣ 中，ＰＡ⊥ＡＣ，ＰＡ 槡＝ ２ ３ ，ＡＣ ＝ ２， ∴ ＰＣ ＝ ４，又 ＡＥ⊥ＰＣ， ∴ ＡＥ ＝ ＡＰ × ＡＣ ＰＣ ＝ 槡２ ３ × ２ ４ 槡＝ ３ ， ∴ ｃｏｓ∠ＥＡＣ ＝ ＡＥ ＡＣ ＝ 槡３ ２ ， ∴ ∠ＥＡＣ ＝ ３０°， ∴ 二面角 Ｅ － ｌ － Ｃ 的大小为 ３０°． １２ 分!!!!!!!!!!!!!!! 高一数学试题参考答案 第 ４ 页（共 ４ 页）