专题05 平面向量-备战2021年高考数学（理）之纠错笔记系列（原卷版）

专题05 平面向量-备战2021年高考数学（理）之纠错笔记系列（原卷版）

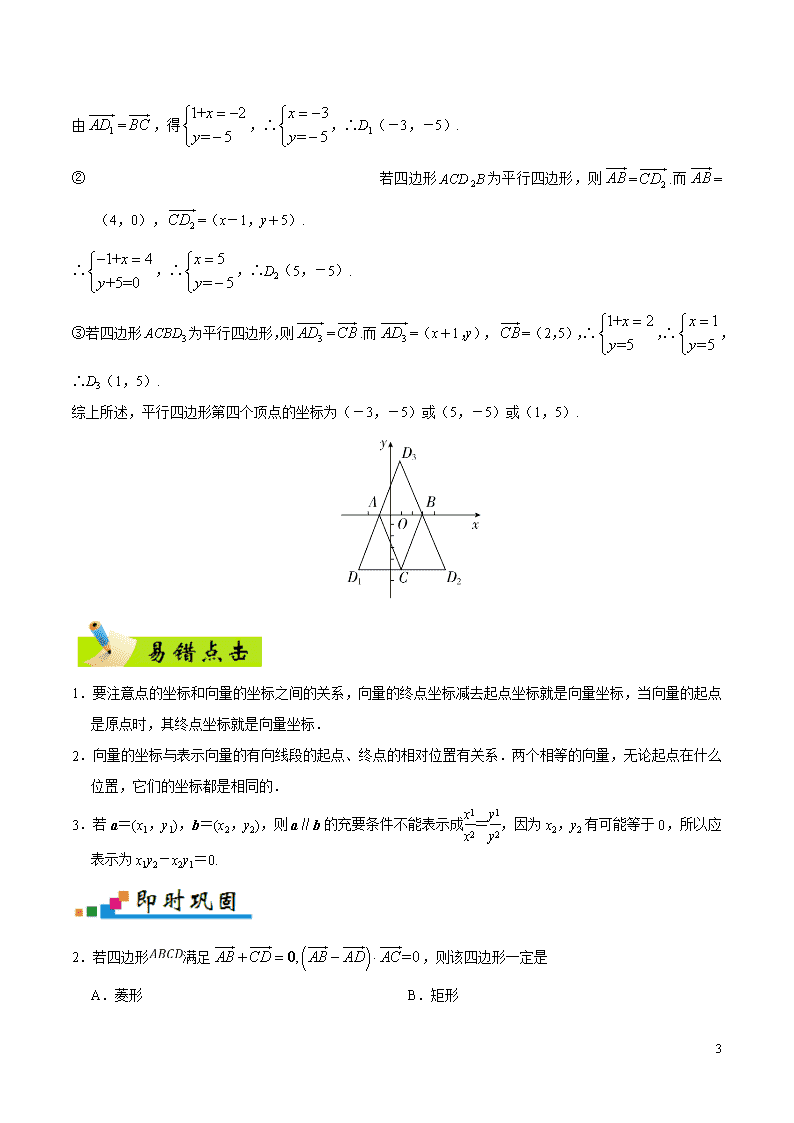
1 专题 05 平面向量 易错点 1 忽略了零向量的特殊性 给出下列命题： ①向量 AB  的长度与向量 BA  的长度相等. ②向量 a 与 b 平行，则 a 与 b 的方向相同或相反. ③两个有共同起点而且相等的向量，其终点必相同. ④零向量与任意数的乘积都为零. 其中不正确命题的序号是 . 【错解】④ 【错因分析】解决向量的概念问题要注意两点：一是不仅要考虑向量的大小，更重要的是要考虑向量的方 向；二是考虑零向量是否也满足条件．要特别注意零向量的特殊性．学%￥科网 【试题解析】① AB  与 BA  是相反向量、模相等，正确；②由零向量的方向是任意的且与任意向量平行，不 正确；③相等向量大小相等、方向相同，又起点相同，则终点相同，正确；④零向量与任意数的乘积都为 零向量，不正确，故不正确命题的序号是②④. 【参考答案】②④ 解决向量的概念问题应关注六点： （1）正确理解向量的相关概念及其含义是解题的关键. （2）相等向量具有传递性，非零向量的平行也具有传递性. （3）共线向量即平行向量，它们均与起点无关. 相等向量不仅模相等，而且方向要相同，所以相等向量一定是平行向量，而平行向量则未必是相等向 量. （4）向量可以平移，平移后的向量与原向量是相等向量.解题时，不要把它与函数图象移动混为一谈. 2 （5）非零向量 a 与 | | a a 的关系： | | a a 是 a 方向上的单位向量. （6）向量与数量不同，数量可以比较大小，向量则不能，但向量的模是非负实数，故可以比较大小. 1．下列命题正确的是 A．     a b a b B．   a b a b C．  ∥a b a b D． 0   0a a 【答案】D 【解析】A 中,两个向量的模相等,但是方向不一定相同,所以不正确； B 中,两个向量不能比较大小,所以错误； C 中,向量平行只能得到方向相同或相反,不能得到向量相等,所以错误； D 中,如果一个向量的模等于 0,则这个向量是 . 易错点 2 忽视平行四边形的多样性失误 已知平行四边形三个顶点的坐标分别为（－1，0），（3，0），（1，－5），求第四个顶点的坐标. 【错解】设 A（－1，0），B（3，0），C（1，－5），D（x，y），∵四边形 ABCD 为平行四边形，∴ AB  = DC  ， 又∵ AB  =（4，0）， DC  =（1－x，－5－y），∴ 1 4 5 =0 x y        ，解得 x=－3，y=－5，∴第四个顶点的坐标为 （－3，－5）. 【错因分析】此题的错解原因为思维定势，错误的认为平行四边形只有一种情形，在解题思路中出现了漏 解.实际上，题目的条件中只给出了平行四边形的三个顶点，并没有给出相应的顺序，故可能有三种不同的 情形. 【试题解析】如图所示，设 A（－1，0），B（3，0），C（1，－5），D（x，y）. 1 若四边形 ABCD1 为平行四边形，则 1AD  = BC  ，而 1AD  = 3 （x＋1，y）， BC  =（－2，－5）. 由 1AD  = BC  ，得 + 2 = 5 1 y x       ，∴ = 5 3x y       ，∴D1（－3，－5）. 2 若四边形 ACD 2B 为平行四边形，则 AB  = 2CD  .而 AB  = （4，0）， 2CD  =（x－1，y＋5）. ∴ + = 1+ 0 4 5 x y     ，∴ = 5 5x y      ，∴D2（5，－5）. ③若四边形 ACBD3 为平行四边形，则 3AD  =CB  .而 3AD  =（x＋1，y），CB  =（2，5），∴ 1+ =5 2 y x    ，∴ =5 1 y x    ， ∴D3（1，5）. 综上所述，平行四边形第四个顶点的坐标为（－3，－5）或（5，－5）或（1，5）. 1．要注意点的坐标和向量的坐标之间的关系，向量的终点坐标减去起点坐标就是向量坐标，当向量的起点 是原点时，其终点坐标就是向量坐标． 2．向量的坐标与表示向量的有向线段的起点、终点的相对位置有关系．两个相等的向量，无论起点在什么 位置，它们的坐标都是相同的． 3．若 a＝(x1，y1)，b＝(x2，y2)，则 a∥b 的充要条件不能表示成x1 x2 ＝y1 y2 ，因为 x2，y2 有可能等于 0，所以应表 示为 x1y2－x2y1＝0. 2．若四边形 满足  , =0AB CD AB AD AC   0      ，则该四边形一定是 4 A．菱形 B．矩形 C．正方形 D．直角梯形 【答案】A 错点 3 忽视两向量夹角的范围 已知向量 (1,2), ( ,1)x a b （1）若 , a b 为锐角，求 x 的取值范围； （2）当 ( 2 ) (2 ) ⊥a b a b 时，求 x 的值. 【错解】（1）若 , a b 为锐角，则 0 a b 且 ,a b 不同向. 2 0x   a b ，∴ 2x   . （2）由题意，可得 2 (1 2 ,4),(2 ) (2 ,3)x x     a b a b ， 又 ( 2 ) (2 ) ⊥a b a b ， (2 1)(2 ) 3 4 0x x     ， 即 22 3 14 0x x    ， 解得 7 2x  或 2x   . 【错因分析】（1）利用向量夹角公式即可得出，注意去掉同方向情况； （2）利用向量垂直与数量积的关系即可得出．. 【试题解析】（1）若 , a b 为锐角，则 0 a b 且 ,a b 不同向. 5 2 0x   a b ，∴ 2x   . 当 1 2x  时， ,a b 同向, 12 2x x   且 . 即若 , a b 为锐角， x 的取值范围是{x| 2x   且 1 2x  }. 【参考答案】（1）{x| 2x   且 1 2x  }；（2） 7 2x  或 2x   . 1.两向量的夹角是指当两向量的起点相同时，表示两向量的有向线段所形成的角，若起点不同，应通过移动， 使其起点相同，再观察夹角． 2.两向量夹角的范围为[0，π]，特别地当两向量共线且同向时，其夹角为 0，共线且反向时，其夹角为π. 3.在利用向量的数量积求两向量的夹角时，一定要注意两向量夹角的范围． 3．已知向量 ( 2, 1), ( ,1)   a b ,且 a 与 b 的夹角为钝角，则实数λ的取值范围是 . 【答案】 1( ,2) (2, )2   【解析】∵ a 与b 的夹角为钝角， ∴ 0 a b ，即 ( 2, 1) ( ,1) 2 1 0        ， ∴ 1 2    . 又当 a 与 b 反向时，夹角为 180°，即 | || |  a b a b ，则 22 1 5 1     ，解得 2  . 应该排除反向的情形，即排除 2  ， 6 于是实数λ的取值范围为 1( ,2) (2, )2   . 【误区警示】依据两向量夹角θ的情况,求向量坐标中的参数时,需注意当夹角为 0°时, cos 1 0   ;当夹角 为 180°时, cos 1 0    ,这是容易忽略的地方. 1．在求 ABC△ 的三边所对应向量的夹角时，要注意是三角形的内角还是外角．如在等边三角形 ABC 中， AB  与 BC  的夹角应为 120°而不是 60°. 2．在平面向量数量积的运算中，不能从 a·b＝0 推出 a＝0 或 b＝0 成立．实际上由 a·b＝0 可推出以下四种 结论：①a＝0，b＝0；②a＝0，b≠0；③a≠0，b＝0；④a≠0，b≠0，a⊥b. 3．实数运算满足消去律：若 bc＝ca，c≠0，则有 b＝a.在向量数量积的运算中，若 a·b＝a·c(a≠0)，则不一定 有 b＝c. 4．实数运算满足乘法结合律，但平面向量数量积的运算不满足乘法结合律，即(a·b)·c 不一定等于 a·(b·c)， 这是由于(a·b)·c 表示一个与 c 共线的向量，而 a·(b·c)表示一个与 a 共线的向量，而 c 与 a 不一定共线． 易错点 4 三角形的“四心”的概念混淆不清 已 知 O 是 平 面 上 的 一 定 点 ， A ， B ， C 是 平 面 上 不 共 线 的 三 个 动 点 ， 若 动 点 P 满 足 + ( + )OP OA AB AC    ，λ∈（0，＋∞），则点 P 的轨迹一定通过 ABC△ 的] A．内心 B．外心 C．重心 D．垂心 【错解】A 【错因分析】对三角形“四心”的意义不明，向量关系式的变换出错，向量关系式表达的向量之间的相互位置 关系判断错误等. 【试题解析】由原等式，得OP OA  = ( + )AB AC   ，即 AP  = ( + )AB AC   ， 根据平行四边形法则，知 +AB AC   是 ABC△ 的中线 AD（D 为 BC 的中点）所对应向量 AD  的 2 倍， 所以点 P 的轨迹必过 ABC△ 的重心，故选 C. 7 【参考答案】C 三角形的“四心”与平面向量 1. 重心. 若点 G 是 ABC△ 的重心，则 + =GA GB GC   0 或 1 ( + )3PG PA PB PC     （其中 P 为平面内任意 一点）.反之，若 + =GA GB GC   0，则点 G 是 ABC△ 的重心. 2. 垂心. 若 H 是 ABC△ 的垂心，则 = =HA HB HB HC HA HC        或 2 2 2 2 2 2 = =HA BC HB AC HC AB        . 反之，若 = =HA HB HB HC HA HC        ，则点 H 是 ABC△ 的垂心. 3. 内 心 . 若 点 I 是 ABC△ 的 内 心 ， 则 有 | | + | | + | |BC IA AC IB AB IC        =0. 反 之 ， 若 | | + | | + | |BC IA AC IB AB IC        =0，则点 I 是 ABC△ 的内心. 4. 外 心 . 若 点 O 是 ABC△ 的 外 心 ， 则 ( ) ( ) ( )OA OB AB OB OC BC OA OC AC                =0 或 | | | | | |OA OB OC    .反之，若| | | | | |OA OB OC    ，则点 O 是 ABC△ 的外心. 4．G 是 ABC△ 的重心，a、b、c 分别是角 A、B、C 的对边，若 3 3aGA bGB cGC   0    ，则角 A  A．90° B．60° C．45° D．30° 【答案】D 【解析】因为 G 是 ABC△ 的重心，所以有GA GB GC   0    .又 3 3aGA bGB cGC   0    ，所以 a∶ b∶ 3 3 c＝1∶1∶1，设 c＝ 3，则有 a＝b＝1，由余弦定理可得，cosA＝1＋3－1 2 3 ＝ 3 2 ，所以 A＝30°，故 选 D. 8 向量与三角形的交汇是高考常见题型，解题思路是用向量运算进行转化，化归为三角函数问题或三角恒等 变形问题或解三角形问题． 一、平面向量的概念及线性运算 1．向量的有关概念 9 2．向量的线性运算 10 3．共线向量定理及其应用 向量 a(a≠0)与 b 共线，当且仅当有唯一的一个实数λ，使得 b=λa. 11 [提醒]限定 a≠0 的目的是保证实数λ的存在性和唯一性． 二、平面向量基本定理及坐标表示 1.平面向量的基本定理 如果 e1，e2 是同一平面内的两个不共线向量，那么对于这一平面内的任意向量 a，有且只有一对实数λ1， λ2，使 a=λ1e1＋λ2e2.其中，不共线的向量 e1，e2 叫做表示这一平面内所有向量的一组基底；把一个向量分 解为两个互相垂直的向量，叫做把向量正交分解.学科网 2.平面向量的坐标表示 在平面直角坐标系中，分别取与 x 轴、y 轴方向相同的两个单位向量 i、j 作为基底，对于平面内的一个 向量 a，由平面向量基本定理知，有且只有一对实数 x、y，使得 a=xi＋yj，这样，平面内的任一向量 a 都可由 x、y 唯一确定，我们把（x，y）叫做向量 a 的坐标，记作 a=（x，y），其中 x 叫做 a 在 x 轴上的 坐标，y 叫做 a 在 y 轴上的坐标. 3.平面向量的坐标运算 （1）向量坐标的求法 ①若向量的起点是坐标原点，则终点坐标即为向量的坐标. ②设 A（x1，y1），B（x2，y2），则 AB  =（x2－x1，y2－y1）. （2）向量加法、减法、数乘向量及向量的模 设 a=（x1，y1），b=（x2，y2），则 a＋b=（x2+x1，y2+y1），a－b=（x1－x2，y1－y2），λa=（λx1，λy1）， |a|= 2 2 1 1+x y ，|a＋b|= 2 2 1 2 1 2( + ) +( + )x x y y . （3）平面向量共线的坐标表示 设 a=（x1，y1），b=（x2，y2），则 a∥b ⇔ x1y2－x2y1=0. （4）向量的夹角 已知两个非零向量 a 和 b，作OA  =a，OB  =b，则∠AOB=θ（0°≤θ≤180°）叫做向量 a 与 b 的夹角.如果向 量 a 与 b 的夹角是 90°，我们说 a 与 b 垂直，记作 a⊥b. 三、平面向量的数量积 1.平面向量的数量积 （1）定义：已知两个非零向量 a 与 b，它们的夹角为θ，则数量|a||b|cos θ叫作 a 与 b 的数量积（或内积）， 记作 a·b，即 a·b=|a||b|cos θ，规定零向量与任一向量的数量积为 0，即 0·a=0. （2）几何意义：数量积 a·b 等于 a 的长度|a|与 b 在 a 的方向上的投影|b|cos θ的乘积. 2.平面向量数量积的运算律 12 （1）a·b=b·a（交换律）. （2）λa·b=λ（a·b）=a·（λb）（结合律）. （3）（a＋b）·c=a·c＋b·c（分配律）. 3.平面向量数量积的性质及其坐标表示 设向量 a=（x1，y1），b=（x2，y2），θ为向量 a，b 的夹角. （1）数量积：a·b=|a||b|cos θ=x1x2＋y1y2. （2）模：|a|= ·a a = 2 2 1 1+x y . （3）设 A（x1，y1），B（x2，y2），则 A，B 两点间的距离|AB|=| |AB  = 2 2 1 2 1 2( ) +( )x x y y  . （4）夹角：cos θ= | | | |   a b a b = 1 2 1 2 2 2 2 2 1 1 2 2 + + + x x y y x y x y . （5）已知两非零向量 a 与 b，a⊥b ⇔ a·b=0 ⇔ x1x2＋y1y2=0，a∥b ⇔ a·b=±|a||b|. （6）|a·b|≤|a||b|（当且仅当 a∥b 时等号成立） ⇔ |x1x2＋y1y2|≤ 2 2 1 1+x y 2 2 2 2· +x y . |a|= 2 2 1 1+x y ，|a＋b|= 2 2 1 2 1 2( + ) +( + )x x y y 四、平面向量的应用 1.向量在平面几何中的应用 若 a=（x1，y1），b=（x2，y2）， （1）a∥b ⇔ a=λb（b≠0） ⇔ x1y2－x2y1=0. （2）a⊥b ⇔ a·b=0 ⇔ x1x2+y1y2=0. （3）cos θ= | | | |   a b a b = 1 2 1 2 2 2 2 2 1 1 2 2 + + + x x y y x y x y . 2.向量在三角函数中的应用 向量与三角的交汇是高考常见题型，解题思路是用向量运算进行转化，化归为三角函数问题或三角恒等 变形问题或解三角形问题. 3.向量在解析几何中的应用 向量在解析几何中的应用，主要是以解析几何中的坐标为背景的一种向量描述.进而利用直线和圆锥曲线 的位置关系的相关知识来解答. 4.向量在物理中的应用 物理学中的力、速度、位移都是矢量，它们的分解、合成与向量的加减法相似，因此可以用向量的知识 13 来解决某些物理问题. 1．已知两点 ，则与向量 AB  同向的单位向量是 A．±（ ） B． C． D． 2．设 M 为平行四边形 ABCD 对角线的交点，O 为平行四边形 ABCD 所在平面内任意一点，则 OA OB OC OD      等于 A．  OM  B． 2OM  C．3OM  D． 4OM  3．已知 ，若 ，则 A． B． C． D． 4．设向量    ,2 , 1, 1x  a b ，且  a b b ，则 x 的值为 A．1 B．2 C．3 D．4 5．（2018 新课标全国Ⅱ理科）已知向量 a ， b 满足| | 1a ， 1  a b ，则 (2 )  a a b A．4 B．3 C．2 D．0 6．（2018 新课标全国Ⅰ理科）设抛物线 C：y2=4x 的焦点为 F，过点（–2，0）且斜率为 2 3 的直线与 C 交于 M，N 两点，则 FM FN  = A．5 B．6 C．7 D．8 7．（2018浙江）已知a，b，e是平面向量，e是单位向量．若非零向量a与e的夹角为 π 3 ，向量b满足b2−4e·b+3=0， 则|a−b|的最小值是 A． 3 −1 B． 3 +1 14 C．2 D．2− 3 8．（2018 年高考新课标Ⅰ卷理科）在 ABC△ 中， AD 为 BC 边上的中线， E 为 AD 的中点，则 EB  A． 3 1 4 4AB AC  B． 1 3 4 4AB AC  C． 3 1 4 4AB AC  D． 1 3 4 4AB AC  9．（2017 年高考北京卷）设 m,n 为非零向量，则“存在负数  ，使得 m n ”是“ 0<m n ”的 A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 10．双曲线 的左，右焦点分别为 ， ， 为右支上一点，且 ，则双曲线的 离心率为 A．3 B．5 C． D． 11．设向量 ， 满足 且 ，则向量 在向量 方向的投影为 A．-2 B．-1 C．1 D．2 12．在 ABC△ 中， 是线段 的三等分点，则 的值为 A． B． C． D． 13．如图，在 ABC△ 中，点 在 边上，且 ，点 在 边上，且 ，则用向量 表示 为 A． B． C． D． 15 14．（2017 年高考浙江卷）如图，已知平面四边形 ABCD，AB⊥BC，AB=BC=AD=2，CD=3，AC 与 BD 交 于点 O，记 1 ·I OAOB   ， 2 ·I OBOC   ， 3 ·I OC OD   ，则 A． 1 2 3I I I  B． 1 3 2I I I  C． 3 1 2I I I  D． 2 1 3I I I  15．（2017 新课标 II 理）已知 ABC△ 是边长为 2 的等边三角形，P 为平面 ABC 内一点，则 ( )PA PB PC    的最小值是 A． 2 B． 3 2  C． 4 3  D． 1 16．（2017 新课标Ⅲ理）在矩形 ABCD 中，AB=1，AD=2，动点 P 在以点 C 为圆心且与 BD 相切的圆上.若 AP AB AD     ，则   的最大值为 A．3 B．2 2 C． 5 D．2 17．（2018 新课标全国Ⅲ理科）已知向量  = 1,2a ，  = 2, 2b ，  = 1,λc ．若  2∥c a + b ，则   ________． 18．平面向量 满足 ，且| |=2，| |=4，则 与 的夹角等于___________． 19．已知向量 ，如果 ∥a b ，那么 的值为___________． 20．（2017 新课标 I 理）已知向量 a，b 的夹角为 60°，|a|=2，|b|=1，则| a +2b |=___________． 21．如图，在矩形 ABCD 中， 2AB  ， 2BC  ，点 E 为 BC 的中点，点 F 在边CD 上，且 2DF FC  ， 则 AE BF  的值是 ．学+科网 16 22．（2017 年高考天津卷）在 ABC△ 中， 60A  ∠ ， 3AB  ， 2AC  ．若 2BD DC  ， AE AC   ( )AB  R  ，且 4AD AE    ，则  的值为___________． 23．在 Rt ABC△ 中， 是 ABC△ 内一点，且 ，若 ，则 的最大值为___________． 24．（2017 年高考山东卷）已知 1 2,e e 是互相垂直的单位向量，若 1 23 e e 与 1 2e e 的夹角为 60，则实数  的值是___________． 25．（2017 年高考浙江卷）已知向量 a，b 满足 1, 2, a b 则   a b a b 的最小值是________，最大值 是___________． 26．（2017 江苏）如图，在同一个平面内，向量OA  ，OB  ，OC  的模分别为 1，1， 2 ，OA  与OC  的夹 角为 ，且 tan =7， OB  与OC  的夹角为 45°．若OC mOA nOB    ( , )m nR ，则 m n  _________． ________________________________________________________________________________________ ________________________________________________________________________________________ 17 ________________________________________________________________________________________ ________________________________________________________________________________________ ________________________________________________________________________________________ ________________________________________________________________________________________ ________________________________________________________________________________________ ________________________________________________________________________________________ ________________________________________________________________________________________ ________________________________________________________________________________________ ________________________________________________________________________________________ ________________________________________________________________________________________