四川省成都市2020届高三下学期第二次诊断考试 理科数学

四川省成都市2020届高三下学期第二次诊断考试 理科数学

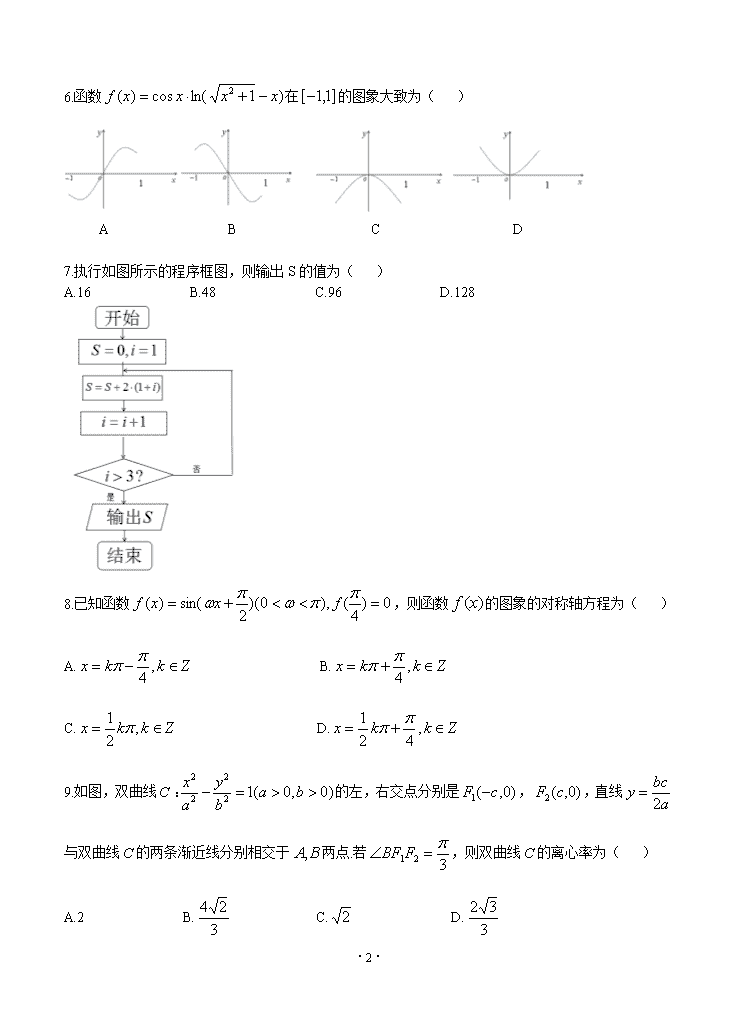
·1· 成都市 2017 级高中毕业班第二次诊断性检测 数学（理科） 本试卷分选择题和非选择题两部分，第 1 卷（选择题）1 至 2 页，第Ⅱ卷（非选择题）3 至 4 页， 共 4 页，满分 150 分，考试时间 120 分钟。 注意事项： 1．答题前，务必将自己的姓名、考籍号填写在答题卡规定的位置上。 2．答选择题时，必须使用 2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干 净后，再选涂其它答案标号。 3．答非选择题时，必须使用 0.5 毫米黑色签字笔，将答案书写在答题卡规定的位置上。 4．所有题目必须在答题卡上作答，在试题卷上答题无效。 5．考试结束后，只将答题卡交回。 第Ⅰ卷（选择题，共 60 分） 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只有一项是 符合题目要求的． 1.复数 z 满足 2)1( iz （i 为虚数单位），则 z 的虚部为（ ） A.i B.-i C.-1 D.1 2.设全集 RU  ，集合  1 xxM ，  2 xxN ，则 NMCU )( =（ ） A. 2xx B. 1xx C. 21  xx D. 2xx 3.某中学有高中生 1500 人，初中生 1000 人，为了解该校学生自主锻炼的时间，采用分层抽样的方法 从高中生和初中生中抽取一个容量为 n 的样本。若样本中高中生恰有 30 人，则 n 的值为（ ） A.20 B.50 C.40 D.60 4.曲线 xxy  3 在点 )0,1( 处的切线方程为（ ） A. 02  yx B. 022  yx C. 022  yx D. 022  yx 5.已知锐角  满足  2cos12sin2  ，则 tan =（ ） A. 2 1 B.1 C.2 D.4 ·2· 6.函数 )1ln(cos)( 2 xxxxf  在 ]1,1[ 的图象大致为（ ） A B C D 7.执行如图所示的程序框图，则输出 S 的值为（ ） A.16 B.48 C.96 D.128 8.已知函数 0)4(),0)(2sin()(   fxxf ，则函数 )(xf 的图象的对称轴方程为（ ） A. Zkkx  ,4  B. Zkkx  ,4  C. Zkkx  ,2 1  D. Zkkx  ,42 1  9.如图，双曲线C )0,0(12 2 2 2  bab y a x： 的左，右交点分别是 )0,(1 cF  ， )0,(2 cF ，直线 a bcy 2  与双曲线C 的两条渐近线分别相交于 BA, 两点.若 321  FBF ，则双曲线C 的离心率为（ ） A.2 B. 3 24 C. 2 D. 3 32 ·3· 10. 在 正 方 体 1111 DCBAABCD  中 ， 点 QP, 分 别 为 ADAB, 的 中 点 ， 过 点 D 作 平 面  使  平面∥，平面∥ QAPB 11 ，若直线 MDB 平面11 ，则 1 1 MB MD 的值为（ ） A. 4 1 B. 3 1 C. 2 1 D. 3 2 11. 已 知 EF 为 圆 1)1()1( 22  yx 的 一 条 直 径 ， 点 ),( yxM 的 坐 标 满 足 不 等 式 组       1 032 01 y yx yx ，则 MFME  的取值范围为（ ） A. ]13,2 9[ B. ]13,4[ C. ]12,4[ D. ]12,2 7[ 12.已知函数 xxexgx xxf  )(,ln)( ，若存在 Rxx  21 ),,0( ，使得 )0()()( 21  kkxgxf 成立，则 kex x 2 1 2 )( 的最大值为（ ） A. 2e B. e C. 2 4 e D. 2 1 e 第Ⅱ卷（非选择题，共 90 分） 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分．把答案填在答题卡上． ·4· 13． 41x  的展开式中 x2 的系数为 。 14．在 △ ABC 中，内角 A，B，C 的对边分别为 a，b，c，已知 3B  ，a=2，b= 3 ，则 △ ABC 的面 积为 。 15．已知各棱长都相等的直三棱柱（侧棱与底面垂直的棱柱称为直棱柱）所有顶点都在球 O 的表面 上，若球 O 的表面积为 28π，则该三棱柱的侧面积为 。 16．经过椭圆 2 2 12 x y  中心的直线与椭圆相交于 M，N 两点（点 M 在第一象限），过点 M 作 x 轴 的垂线，垂足为点 E，设直线 NE 与椭圆的另一个交点为 P．则 cos∠NMP 的值是 。 三、解答题：本大题共 6 小题，共 70 分，解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分 12 分） 已知 na 是递增的等比数列，a1=1，且 2a2， 3 3 2 a ， 4a 成等差数列． （Ⅰ）求数列 na 的通项公式； （Ⅱ）设 2 1 2 2 1 log logn n n b a a    ， n N  。求数列{bn}的前 n 项和 Sn． 18．（本小题满分 12 分） 如图，在四棱锥 P-ABCD 中，O 是边长为 4 的正方形 ABCD 的中心，PO⊥平面 ABCD，E 为 B C 的中点． ·5· （Ⅰ）求证：平面 PAC⊥平面 PBD （Ⅱ）若 PE=3，求二面角 D 一 PE 一 B 的余弦值． 19．（本小题满分 12 分） 某动漫影视制作公司长期坚持文化自信，不断挖据中华优秀传统文化中的动漫题材，创作出一 批又一批的优秀动漫影视作品，获得市场和广大观众的一致好评，同时也为公司赢得丰厚的利润．该 公司 2013 年至 2019 年的年利润 y 关于年份代号 x 的统计数据如下表（已知该公司的年利润与年份 代号线性相关）： 年份 2013 2014 2015 2016 2017 2018 2019 年份代号 x 1 2 3 4 5 6 7 年利润 y（单位：亿元） 29 33 36 44 48 52 59 （Ⅰ）求 y 关于 x 的线性回归方程，并预测该公司 2020 年（年份代号记为 8）的年利润； （Ⅱ）当统计表中某年年利润的实际值大于由（Ⅰ）中线性回归方程计算出该年利润的估计值 时，称该年为 A 级利润年，否则称为 B 级利润年，将（Ⅰ）中预测的该公司 2020 年的年利润视作该 年利润的实际值，现从 2013 年至 2020 年这 8 年中随机抽取 2 年，求恰有 1 年为 A 级利润年的概率． ·6· 参考公式： xbya xx yyxx b n i i n i ii ˆˆ, )( ))(( ˆ 1 2 1         20．（本小题满分 12 分） 已知椭圆 )0,0(12 2 2 2  bab y a xE： 的左，右焦点分别为 F1（-1，0），F2（1，0），点 P 在椭 圆 E 上，PF2⊥F1F2，且|PF1|=3|PF2|． 等守其，平 （Ⅰ）求椭圆 E 的标准方程； （Ⅱ）设直线 l：x=my+1（m∈R）与椭圆 E 相交于 A，B 两点，与圆 x2+y2=a2 相交于 C，D 两 点，求|AB|·|CD|2 的取值范围． 21．（本小题满分 12 分） 已知函数 )1ln(2)( 2  xmxxxf ，其中 m∈R． （Ⅰ）当 m>0 时，求函数 f（x）的单调区间； （Ⅱ）设 xexfxg 1)()(  ，若 1 1)(  xxg ，在 ),0(  上恒成立，求实数 m 的最大值． 请考生在第 22，23 题中任选择一题作答，如果多做，则按所做的第一题记分作答时，用 2B 铅 笔在答题卡上把所选题目对应的标号涂黑． 22．（本小题满分 10 分）选修 4-4：坐标系与参数方 在平面直角坐标系 xOy 中，曲线 C 的参数方程为      my mx 2 2 （m 为参数）．以坐标原点 O 为极点， ·7· x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为 01cossin   ． （Ⅰ）求直线 l 的直角坐标方程与曲线 C 的普通方程； （Ⅱ）已知点 P（2，1）设直线 l 与曲线 C 相交于 M，N 两点，求 PNPM 11  的值． 23．（本小题满分 10 分）选修 4-5；不等式选讲） 已知函数 f（x）=|x-1|+|x+3|． （Ⅰ）解不等式 f（x）≥6； （Ⅱ）设 g（x）=-x2+2ax，其中 a 为常数若方程 f（x）=g（x）在（0，+∞）上恰有两个不相等的实 数根，求实数 a 的取值范围． 答案 第一卷 1C 2A 3B 4D 5C 6B 7B 8C 9A 10B 11D 12C 第二卷 13. 6 14. 2 3 15. 36 16. 0 ·8· ·9· ·10· ·11· ·12·