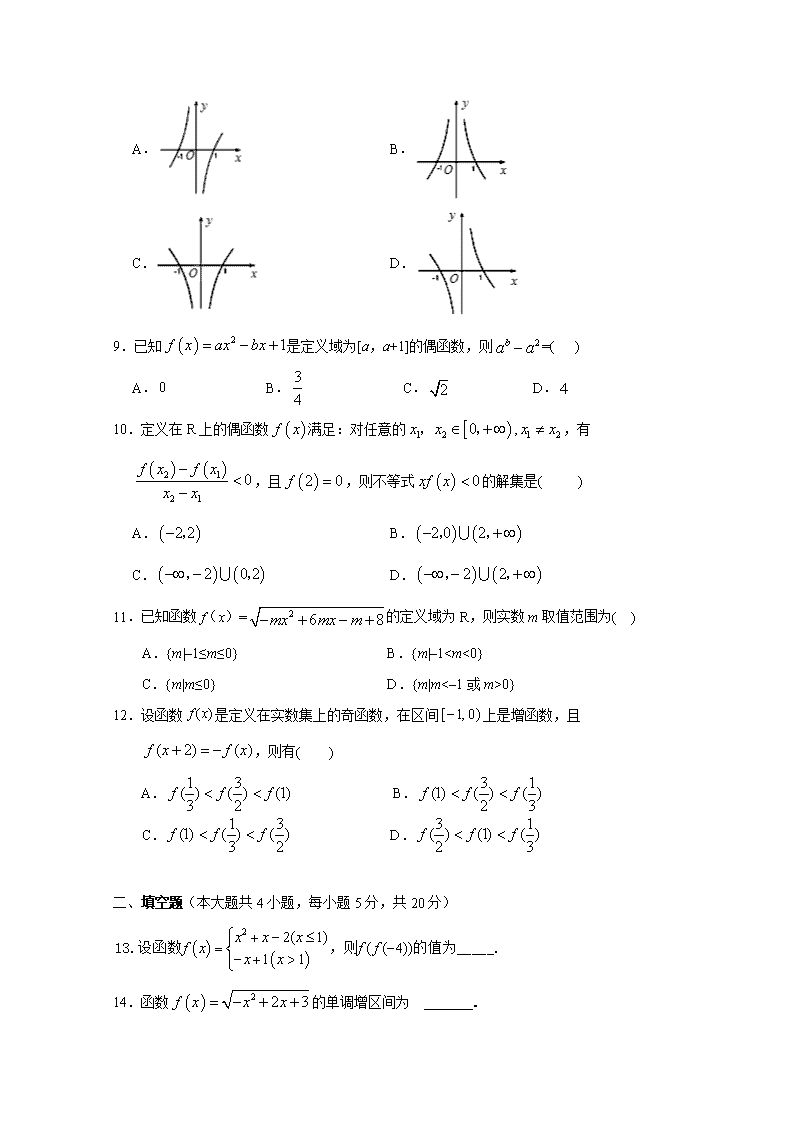黑龙江省黑河市嫩江县高级中学2019-2020学年高一第一次月考数学试卷

黑龙江省黑河市嫩江县高级中学2019-2020学年高一第一次月考数学试卷

www.ks5u.com 数学 一、 选择题（本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．已知全集，集合则等于（ ）‎ A． B． C． D．‎ ‎2．下列各组中的表示同一集合的是( )‎ ‎①； ②；‎ ‎③；④‎ A．① B．② C．③ D．④‎ ‎3.设，集合= ( )‎ A．1 B．－‎1 ‎C．2 D．－2‎ ‎4．下列各组函数中，表示同一个函数的是( )‎ A．与 B． 与 C．与 D．与 ‎5．已知f（）=，则f（x）的解析式为（ ）‎ A． B．‎ C． D．‎ ‎6．已知函数在闭区间上有最大值5，最小值1，则的取值范围是（ ）‎ A． B． C． D．‎ ‎7．已知的定义域为，则的定义域是( )‎ A． B． C． D．‎ ‎8．函数y=的图象是( )‎ A． B．‎ C． D．‎ ‎9．已知是定义域为[a，a+1]的偶函数，则=( )‎ A． B． C． D．‎ ‎10．定义在R上的偶函数满足：对任意的，有，且，则不等式的解集是( )‎ A． B． ‎ C． D．‎ ‎11．已知函数f（x）=的定义域为R，则实数m取值范围为( )‎ A．{m|–1≤m≤0} B．{m|–10}‎ ‎12．设函数是定义在实数集上的奇函数，在区间上是增函数，且，则有( ) ‎ A． B．‎ C． D．‎ 一、 填空题（本大题共4小题，每小题5分，共20分） ‎ ‎ ‎ ‎14．函数的单调增区间为 _______. ‎ ‎15已知，若，则 _______. ‎ ‎______ .‎ 一、 解答题（17题10分，18—22题每题12分，共70分.解答应写出文字说明、证明过程或演算步骤）‎ ‎17．已知,，且，求实数组成的集合 ‎18.已知集合A={x|1＜x＜6}，B={x|2＜x＜10}，C={x|5−a＜x＜a}．‎ ‎19．已知函数满足.‎ ‎（1）求，的值；‎ ‎（2）求函数在区间上的最值.‎ ‎20．已知函数.‎ ‎（1）若为偶函数，求在上的值域；‎ ‎（2）若在区间上是减函数，求在上的最大值.‎ ‎21.已知函数y=f (x)是定义在R上的奇函数，且当x≥0时，f (x)=-x2+ax.‎ ‎（1）若a=-2，求函数f (x)的解析式；‎ ‎（2）若函数f (x)为R上的单调减函数，‎ ‎①求a的取值范围;‎ ‎②若对任意实数m,f (m-1)+f (m2+t)<0恒成立，求实数t的取值范围.‎ ‎22.已知函数f(x)对任意的实数m，n都有：f(m＋n)＝f(m)＋f(n)－1，‎ 且当x＞0时，有f(x)＞1.‎ ‎(1)求f(0)．‎ ‎(2)求证：f(x)在R上为增函数．‎ ‎(3)若f(1)＝2，且关于x的不等式f(ax－2)＋f(x－x2)＜3对任意的x∈[1，＋∞)恒成立，求实数a的取值范围．‎ 答案 一． 选择题 ‎1.A2.C3.C4.C5.D6.D7.D8.A9B10.B11.A12.A 二．填空题 ‎13.-914.[-1,1]15.-2616.‎ 三．解答题 ‎17．【答案】C＝{0,1 ,2}‎ ‎【解析】‎ ‎【分析】‎ 首先通过解一元二次方程，得带集合A，根据空集的概念，以及包含关系的本质所在，需要对B进行分类讨论，按两种情况进行讨论，从而求得结果 ‎【详解】‎ 由x2－3x＋2＝0，得x＝1，或x＝2.‎ ‎∴A＝{1,2}．∵B⊆A，∴对B分类讨论如下：‎ ‎(1)若B＝∅，即方程ax－2＝0无解，此时a＝0.‎ ‎(2)若B≠∅，则B＝{1}或B＝{2}．‎ 当B＝{1}时，有a－2＝0，即a＝2；‎ 当B＝{2}时，有2a－2＝0，即a＝1.‎ 综上可知，符合题意的实数a所组成的集合C＝{0,1 ,2}‎ ‎18.【答案】（1）A∪B={x|1＜x＜10}，（）∩B={x|6≤x＜10}；（2）（−∞，3].‎ ‎【解析】（1）由A={x|1＜x＜6}，B={x|2＜x＜10}，可得A∪B={x|1＜x＜10}，‎ ‎∵={x|x≤1或x≥6}，‎ ‎∴（）∩B={x|6≤x＜10}.‎ ‎（2）由题知C⊆B，‎ ‎①C=∅时，5−a≥a；‎ ‎∴；‎ ‎②C≠∅时，则，‎ 解得，‎ 综上得，a≤3.‎ ‎∴a的取值范围是（−∞，3]．‎ ‎19.．【答案】（1）；（2）最小值为，最大值为4．‎ ‎【解析】（1）因为．‎ 所以，‎ 所以，‎ 解得.‎ ‎（2）由（1）可知：． ‎ 所以． ‎ 当时，取最小值 ； ‎ 当时，取最大值4‎ ‎20．【答案】（1）；（2）.‎ ‎【解析】（1）因为函数为偶函数，‎ 故，得.‎ 所以，‎ 因为，‎ 所以，即值域为：. ‎ ‎（2）若在区间上是减函数，则函数图象的对称轴为，‎ 因为，‎ 所以时，函数递减，时，函数递增，‎ 故当时，，‎ ‎， ‎ ‎，‎ 由于，‎ 故在上的最大值为.‎ ‎21．【答案】(1) .‎ ‎(2) ①a≤0. ②t> .‎ ‎【解析】‎ 本试题主要是考查了抽象函数的解析式的求解和单调性的证明以及解不等式。‎ ‎（1）因为当时，，又因为为奇函数，所以，进而得到解析式。‎ ‎（2）根据函数单调性，对于参数a分为正负来讨论得到取值范围。‎ ‎（3）因为，∴ 所以是奇函数，∴，而又因为为上的单调递减函数，所以恒成立，分离参数的思想得到范围。‎ ‎（1）当时，，又因为为奇函数，‎ 所以 所以…………………………6分 ‎（2）①当时，对称轴，所以在上单调递减，‎ 由于奇函数关于原点对称的区间上单调性相同，所以在上单调递减，‎ 又在上，在上，‎ 所以当a0时，为R上的单调递减函数 当a>0时，在上递增，在上递减，不合题意 所以函数为单调函数时，a的范围为a………………………………………….10分 ‎②因为，∴ 所以是奇函数，∴…………………………12分 又因为为上的单调递减函数，所以恒成立，…………………14分 所以恒成立， 所以…………………………16‎ ‎22．【答案】(1) f(0)＝1 (2)见解析 (3) (－∞，2－1)‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用赋值法，令，可得．（2）根据函数单调性的定义并结合所给的函数的性质可证明结论成立．（3）根据题意可将不等式化为，再由函数f(x)在R上为增函数可得x2-(a+1)x+3>0对任意的x∈[1,+∞)恒成立，然后根据二次函数在所给区间上的最值的求法求出函数的最小值后可得所求．‎ ‎【详解】‎ ‎(1)解令m=n=0,则f(0)=‎2f(0)-1,‎ ‎∴f(0)=1.‎ ‎(2)证明：设x1,x2∈R,且x1f(x1)．‎ 故f(x)在R上为增函数．‎ ‎(3)解∵，‎ 即，‎ ‎∴，‎ ‎∵f(1)=2,‎ ‎∴.‎ 又f(x)在R上为增函数,‎ ‎∴．‎ ‎∴对任意的x∈[1,+∞)恒成立.‎ 令，‎ ‎①当≤1,即a≤1时,函数在[1,+∞)上单调递增，‎ 由,得a<3,‎ ‎∴a≤1；‎ ‎②当>1,即a>1时,由,得，‎ ‎∴ 综上可得实数a的取值范围为．‎ ‎ ‎